Blob Models of Confined Polymer Chains

A real polymer chain with excluded volume is more extended in a confined space than one in free space, which leads to a reduction of entropy since fewer conformations are available to the segments, whereas an ideal chain will assume a more compact configuration since the segments are reflected at the barriers.
An exact theoretical treatment of this problem is very difficult. However, when using the blob model, it is possible to obtain at least asymptotic scaling relationships between the entropy and the chain length for sufficiently long chains confined in a simple geometrical arrangement.

Polymer Chain in a Tube - Biaxial Compression

Let us consider a real chain consisting of N segments of size l confined to a cylindrical tube or pore of diameter D. When the radius of gyration in the free solution (Rg) is much smaller than the pore size, the chain conformations are not much affected by the tube wall. As Rg exceeds D, however, the chain is forced to adopt conformations extended in the direction of the cylinder due to excluded volume effects. For even smaller pores the confined chain can be envisioned as a train of blobs of diameter D along the pore channel.

Real chain confined in a cylindrical pore

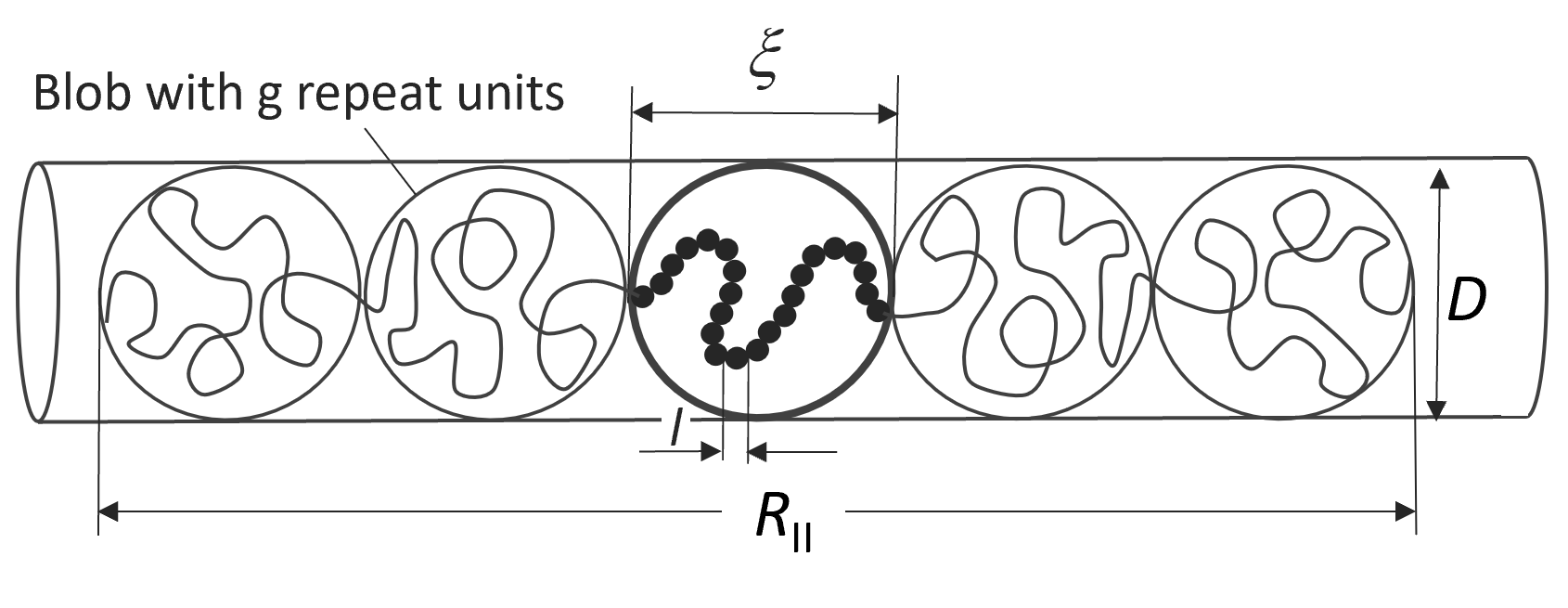
CROW logo

According to the blob model, the repeat units in each sphere assume a conformation of a real chain in the absence of any confinement. Then the size of the subchains ξ in the compression blobs, which is assumed to be equal to the tube diameter D, follows the same scaling laws as those of free chains

D = ξ ≈ l g3/5   or   g ≈ (D/l)5/3

The average length of the polymer chain in the tube R|| is equal to the product of the number of blobs N/g and their size D:1

R|| ≈ D N/g ≈ (l/D)2/3Nl

Thus the length of a polymer chain squeezed into a tube is linear proportional to the number of repeat units N. Furthermore, the concentration inside the chain scales according to2

cPore ≈ N / (D2R||) ≈ l-3 (l/D)4/3

and is independent of number of segments N. Let us know calculate the free energy required to squeeze a chain into a tube. This energy is assumed to be equal to the product of the number of blobs N/g and the free energy of confinement per blob which is of the order kT:1-3

F(N, D) / kT ≈ N/g ≈ N (l/D)5/3 ≈ (RF/D)5/3

This scaling relationship can be generalized to biaxial confinement of chains with fractal dimension 1/ν, as has been shown by Colby and Rubinstein:3

F(N, D) / kT ≈ (lNν/D)1/ν

For example, the fractal dimension of a chain in a θ-solvent is ν = 1/2 (ideal chain). Then the scaling relation for confinement reads:

F(N, D) / kT ≈ N (l/D)2 ≈ (R0/D)2

Note, the confinement energy of a chain in an athermal solvent is larger than that of one in a θ-solvent.

Polymer Chain in a Slit - Uniaxial Compression

A real polymer chain in a slit of width D can be described as a blob arrangement where the motion of the blobs is restricted to the slit. This situation is equivalent to a two-dimensional self-avoiding walk:4

R2D ≈ l N3/4

By replacing l with D and N with N/g, we obtain1,5

R|| ≈ D (N/g)3/4 ≈ N3/4l (l/D)1/4

The smallest slit width D corresponds to the Kuhn monomer size l. In this case, the entire polymer chain scales like a two-dimensional self-avoiding walk:6

R|| ≈ l N3/4

Real chain confined between to plates

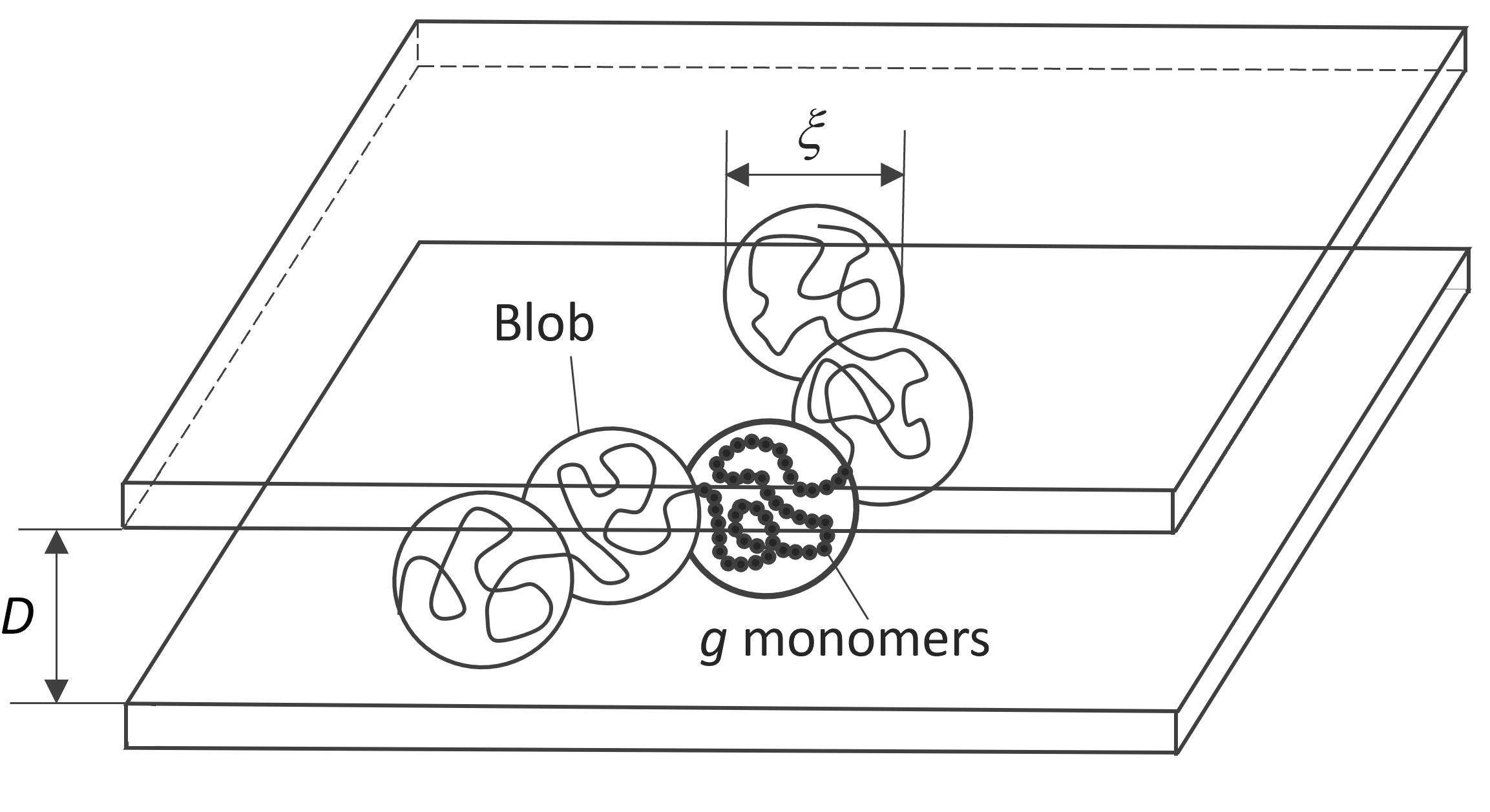
CROW logo

 

Note, the same result can be derived from Flory's excluded volume theory when replacing the excluded volume with the excluded area of a blob which is equal to D2. Then the repulsive interaction energy of N/g compression blobs is given by3

Fint / kT ≈ D2 (N/g2) / R||

and the entropic part of the free energy of the blob arrangement3

Fent / kT ≈ R||2 / (N/gD2)

Minimizing the free energy F = Fent + Fint with respect to R||2 gives the same scaling relationship.

References, Notes & Further Readings
  1. M. Daoud and P.G. de Gennes, J. Physique 38, 85 (1977)
  2. P.G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press (1970)
  3. M. Rubinstein and R. Colby, Polymer Physics, 1st Ed., Oxford University Press (2003)
  4. C. A. J. Hoeve, J. Chem. Phys. 44, 1505 (1965)
  5. P.G. de Gennes, J. Physique 37, 1445 (1976)
  6. The scaling exponent ν = 3/4 is universal for two-dimensional walks with excluded volume interaction.
  7. M. Doi, Introduction to Polymer Physics, Oxford Science Publications (1995)
  8. I. Teraoka, Polymer Solutions: An Introduction to Physical Properties, John Wiley (2002)
  9. A. Y. Grosberg, A.R. Khokhlov, Statistical Physics of Macromolecules, AIP Press (1994)

October 12, 2021

  • Summary

    Confined Chains

    Ideal or Gaussian chains assume closely packed conformations in confined space due to unhindered chain folding, while real chains are more extended in confinement than in free space due to excluded volume interaction.

  • The behavior of compressed polymers can be described with the blob model. A blob represents the unit of chain length that is swollen, i.e., the average unit length that is not overlapping with other polymer chains nearby.

  • The size of the compression blobs in narrow pores or narrow slits is assumed to be equal to the pore diameter or slit width.

Read More

 

  • Polymer chains trapped in small pores can be envisioned as an linear array of compression blobs that are fully aligned along the pore channel.

  • On length scales smaller than the compression blob size, the polymer chains are unperturbed, whereas the arrangement of the blobs themselves is constrained by the confinement.

  • The free energy of confinement of a polymer chain trapped in a narrow pore is of the order kT per compression blob.

  • The decrease in entropy is due to the restriction of the degrees of freedom of the blobs in the pore and grows linearly with the chain length N.

  • The confinement energy of a polymer chain in an athermal solvent is larger than that of a polymer chain in a θ-solvent.