Polymers Modeled as Loop-erased Walks on Simple Cubic Lattice

A polymer in an athermal solvent can be modeled as a self-avoiding walk (SAW) on a lattice. This model is very popular and has been used to describe the dynamic behavior of idealized polymer chains in solution both analytically and numerically. Because of its great importance, the SAW problem has been studied by scientist and mathematicians for more than half a century. So far, it has defied exact analytical solution. To solve SAW problems one can either make use of algebraic recursion equations1-3 or of direct enumeration techniques.4-8 Both methods allow for the exact calculation of several SAW properties such as the total number of self-avoiding walks, cN, and the mean square end-to-end distance, ⟨RN2〉. But these methods are only feasible for very short walks (i.e. short lattice chains) due to the dramatic increase in computation time with increasing chain length. In contrast, Monte Carlo methods are well suited for generating long self-avoiding walks, but these methods allow only for approximate counting of self-avoiding walks.9

The (exact or approximate) number of self-avoiding walks, cNSAW, on a lattice can be calculated by a simple application of the inclusion-exclusion principle from combinatorics,11 which erases all walks that self-intersect, i.e. that form loops of any possible size. This is possible if all cumulative probabilities ΦN (L2i+2) that a random walk forms at least one loop of size n = 2i + 2 but no loops of size n ≤ 2i are known. Then the probability that a walk does not form any loop, i.e. is fully self-avoiding, can be calculated from

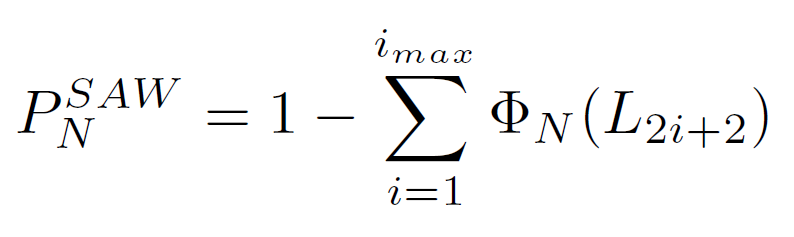
Each cumulative probability ΦN (L2i+2) can be written in the form:

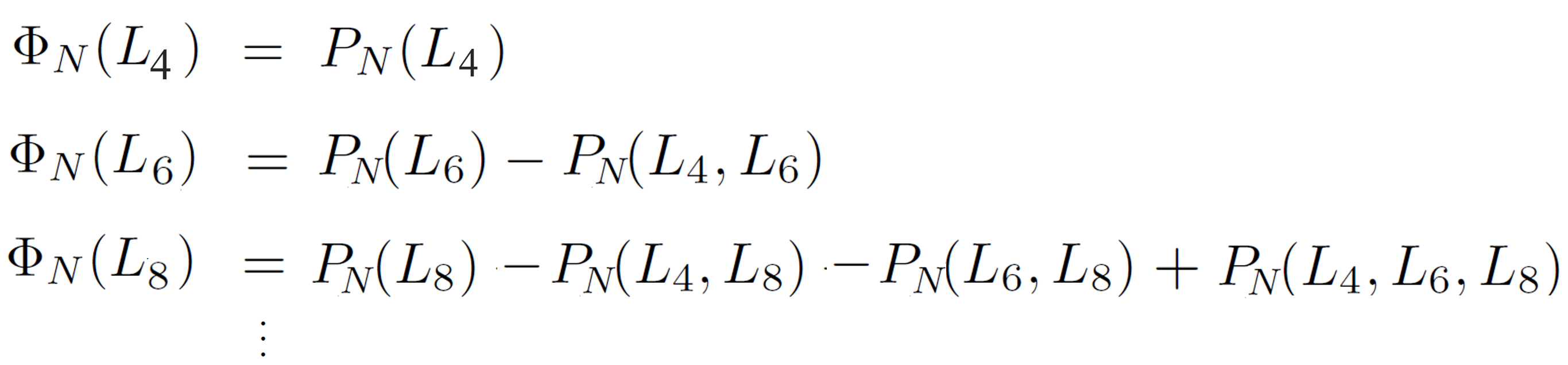
where PN ({Ls, Lt, Lu, ...}) are the probabilites that a non-reversal walk forms at least one loop of size s, t, u,... Obviously, the number of terms increases dramatically with increasing length of the walk. For example, for a walk of N = 20 steps, 255 probabilities have to be calculated. Therefore, for very large N, the number of SAWs has to be either calculated by a computer or the cumulative probability ΦN (L2i+2) have to be estimated from a limited set of loops. For example, if we neglect loops of size s ≥ 10, the probability that a walk of N steps does not form any loop of size 4 - 8 reads:

 

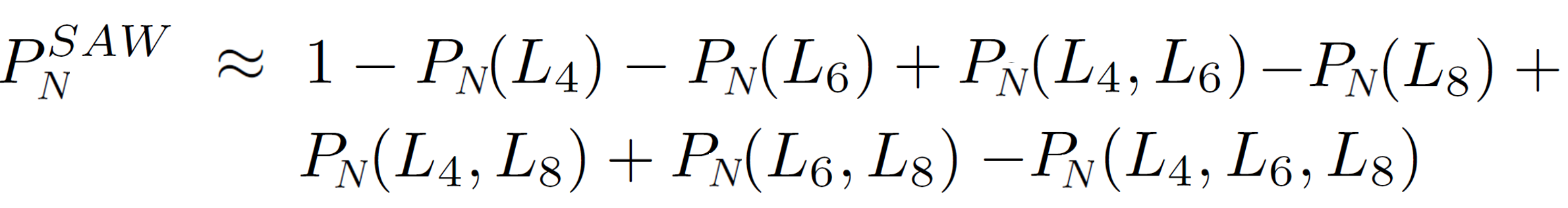
Types of Loops in Random Walks

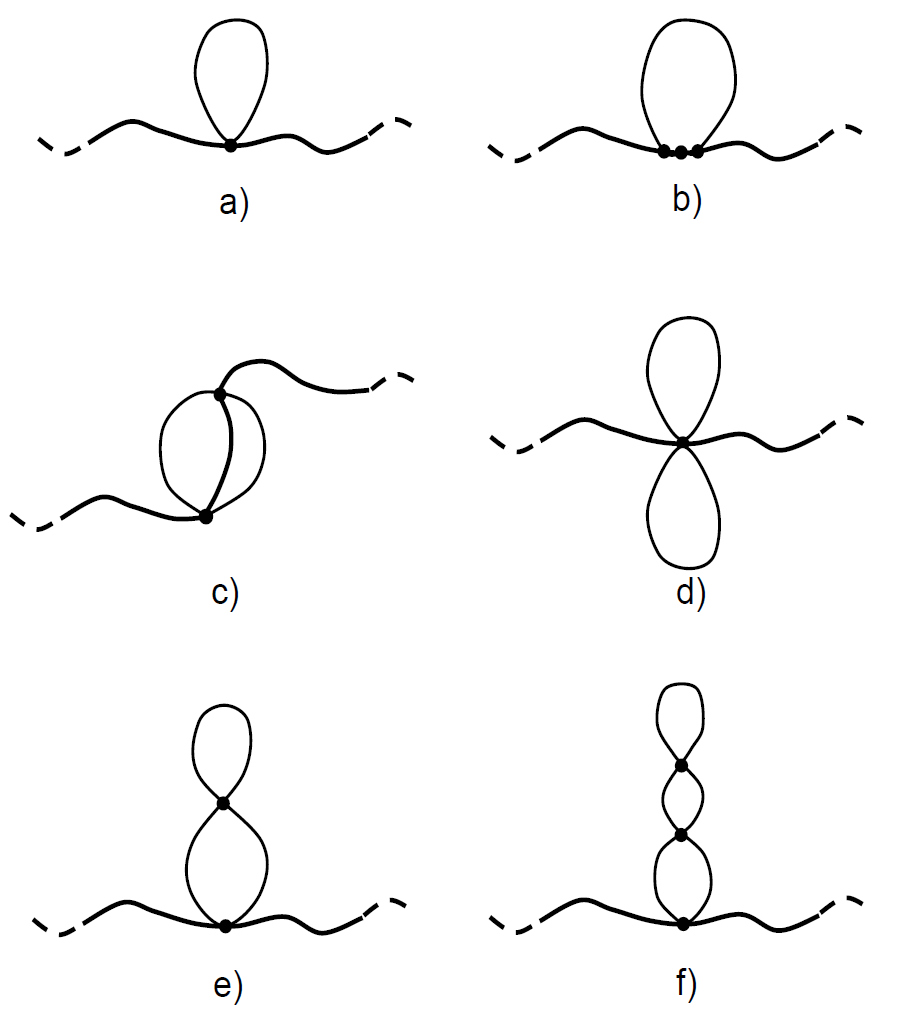
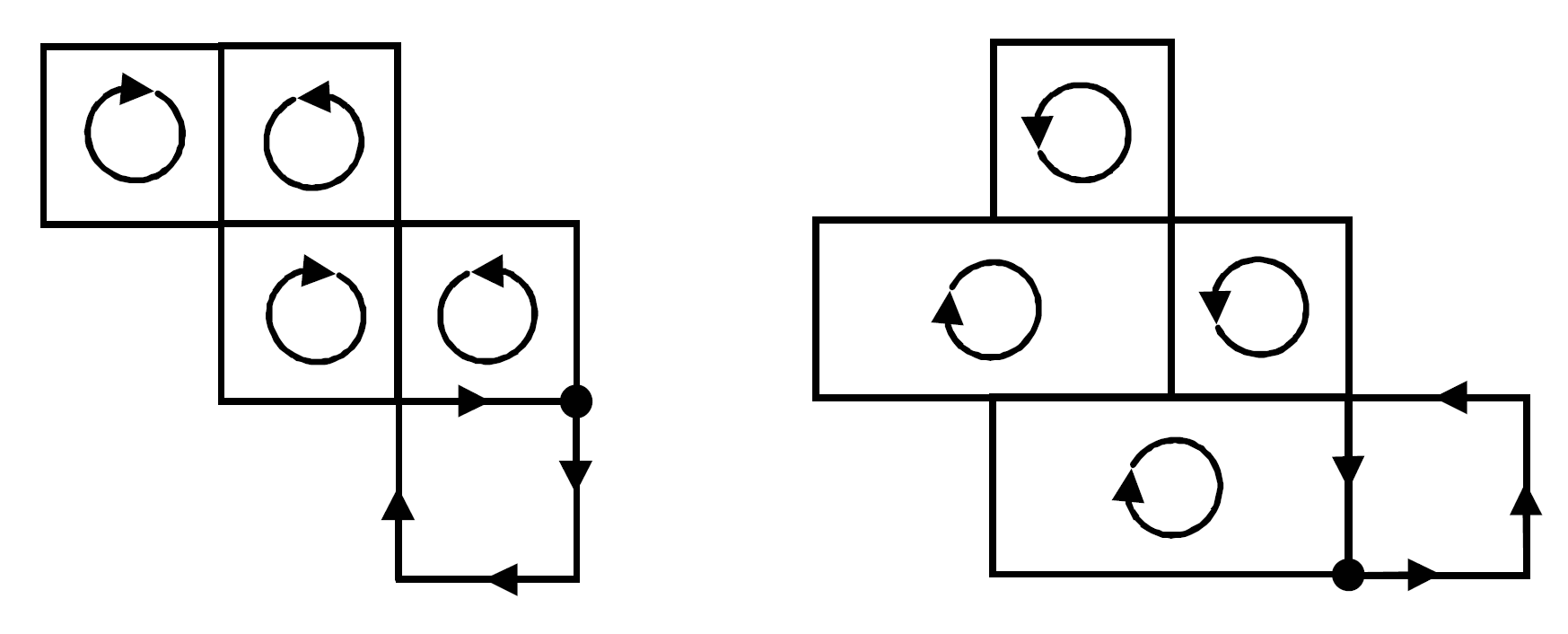
Note that small loops are much more abundant than large loops. In other words, the probability that a long random walk forms at least one large loop is very small compared to the probability that a walk forms at least one or more small loops. As will be shown below, erasing only walks with loops of size 4, 6 and 8 only slightly under- or overestimates the exact enumeration results computed by MacDonald et al. and Lin et al.8, 12 For this case, only probabilities up to order three, PN(Ls), PN(Ls, Lt) and PN(Ls, Lt, Lu), are needed to estimate cNSAW. To simplify the calculations, we assume that a second loop walk does not begin inside another loop walk. In other words, none of the steps of a loop are part of a preceding or succeeding loop walk and so on, i.e. loops of type (c), as depicted in the figure above, can be neglected. Then in a first approximation, only walks that form simple loops such as (a) and (b) need to be erased to estimate cNSAW. As will be shown, this is a reasonable assumption for short walks.13 The derivation of the loop probabilities PN ({Li}), even for this simplified problem, is rather complicated and the details are omitted. For the simple case {Li} = Ls the final result reads

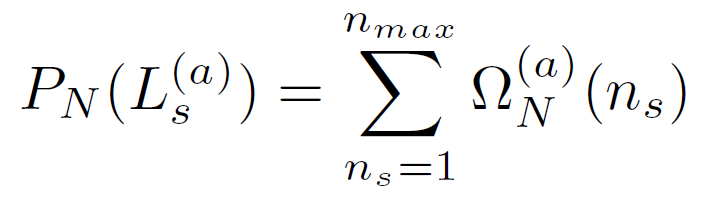
with

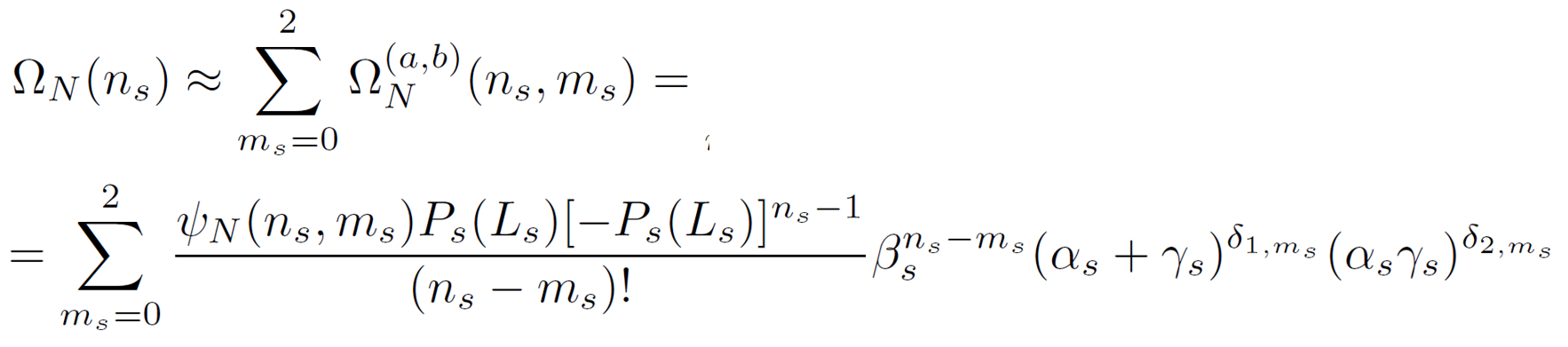
and

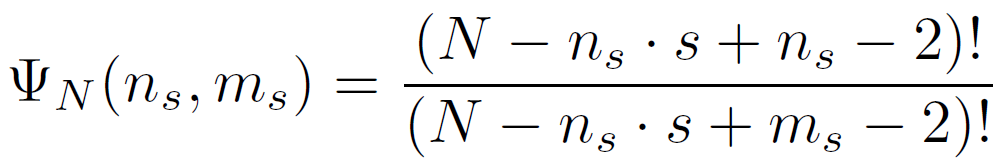
where ΨN (ns, ms) is the number of distinguishable ways to insert ns loops of size s in-between the remaining N - ns - ms steps of a NRW with ms terminal loops of size s; Ps(Ls) is the probability that a self-avoiding walk of s steps revisits the site from which it started; and αs, βs and γi are the conditional probabilities that a terminal loop, a loop inserted in-between any two steps and a loop at the beginning of a walk, respectively, are part of a non-reversal walk. These three probabilities can be estimated from15

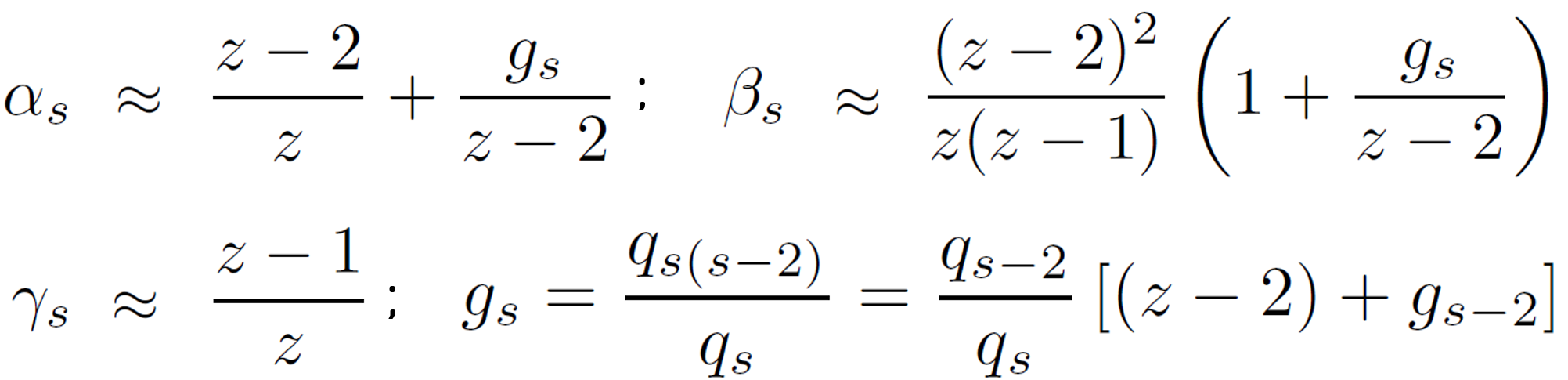
where z = 6 is the coordination number (2 x space dimensionality), qs is the number of non-reversal loop walks of size s, and gi is the probability that the first and last step of a loop are antiparallel to each other (g4 = 0). Note, for very long walks, the first term of ΩN ({ni}) becomes much larger than the last two terms, i.e. ΨN ({ni}, 0) is the leading term.

 

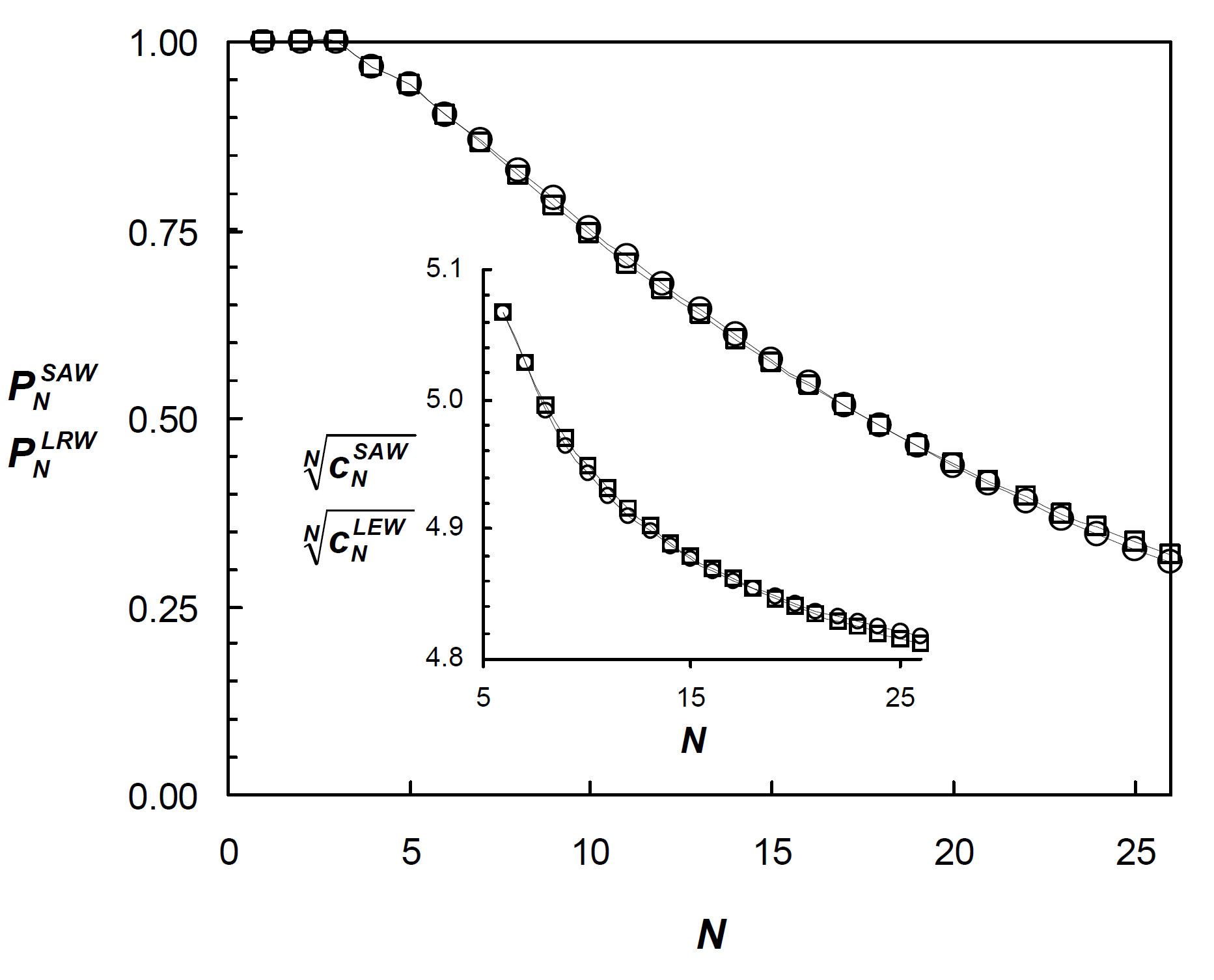
        PN of SAWs8 (○) and LEWs (□) plotted against N

  SHOW CNSAW  

The probability PN(Ls, Lt,...) that a walk forms any number of loops of type Ls, Lt,... is the sum of the probabilities ΩN(ns; nt,..) over all subsets of loop numbers {ns, nt,...}, ni ≥ 1:

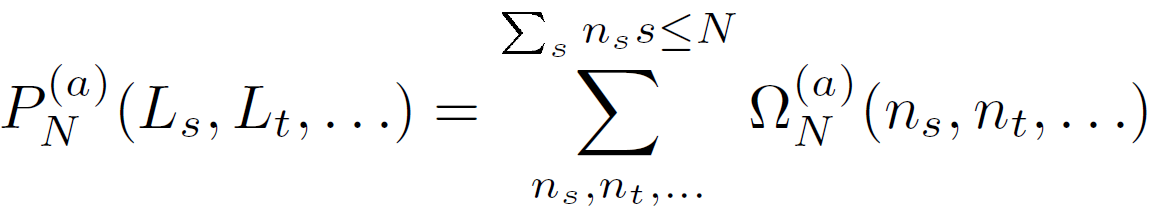
For example, for {Li} = Ls, the probability PN (Ls) that a non-reversal walk forms any number of loops of size s reads13,14

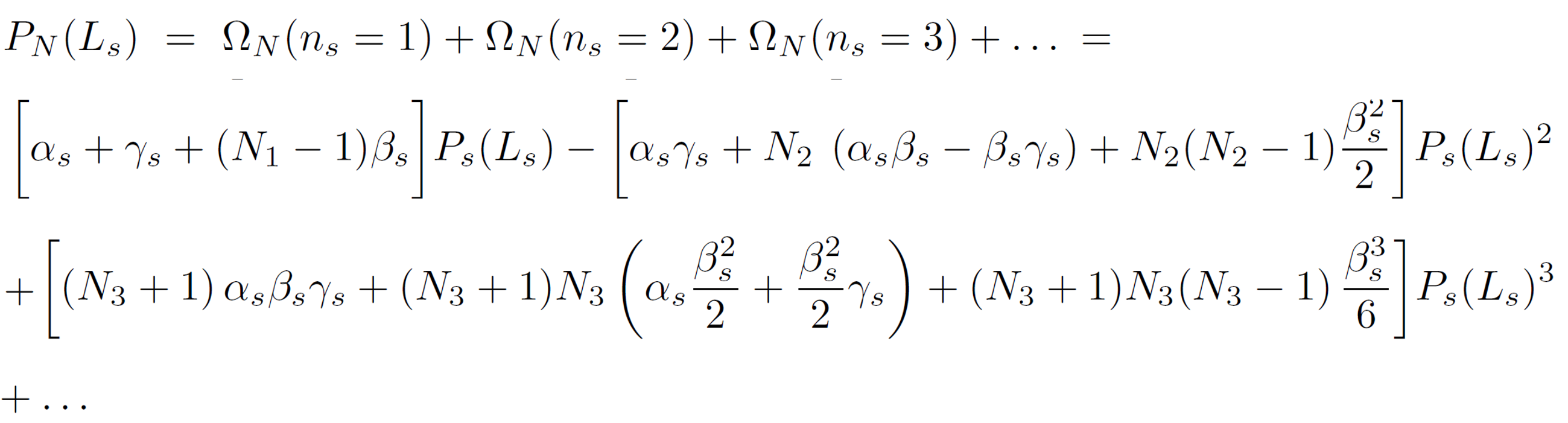
where Ni = N - i·s > 0 the number of steps that are not part of any loop of size s and ns, max < N / s. Similar expressions can be derived for a sets of loops, A = {Li, Lj, ...}. Below, only walks forming loops of 4, 6 and 8 steps will be erased. Then only the probabilities PN(Ls), PN(Ls, Lt), and PN(Ls, Lt, Lu) need to be calculated.

To date, no method has been developed to calculate the exact number of self-avoiding walks, cNSAW, for any number of steps N. In fact, cNSAW has been successfully enumerated for only short SAWs. It can be shown that for long walks (N → ∞), PN(Ls) satisfies the scaling relation

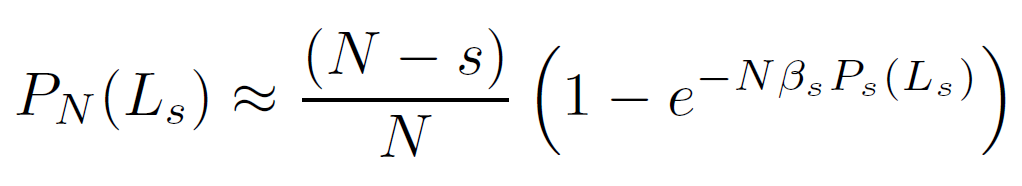
This means, if N is large and s << N, the function PN(Ls) is close two unity, but never exact unity since there are always some walks that do not intersect. Therefore, erasing walks that form at least one short loop of s ≤ smax gives a first estimate of cNSAW. In fact, for very short walks, N < 7, the exclusion of loops of type (a) and (b)  with 4 and 6 vertices gives the exact values of cNSAW since these are the only loops that occur in such a walk. For example, for the SAW probability of 4 to 6 steps we obtain from the equation above:

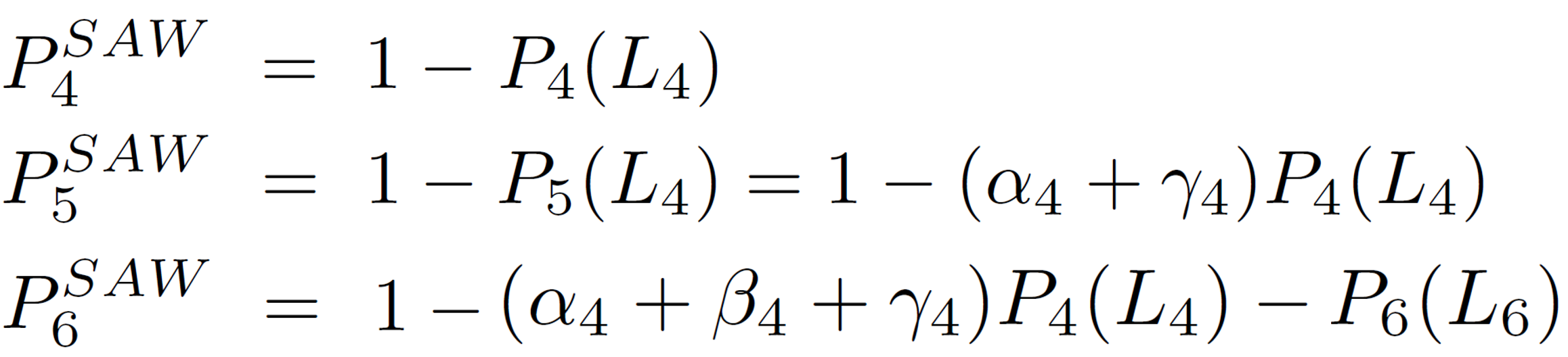
Since cNSAW = PNSAWz(z-1)N-1, the number of self-avoiding walks cNSAW can be written as polynomials in z:

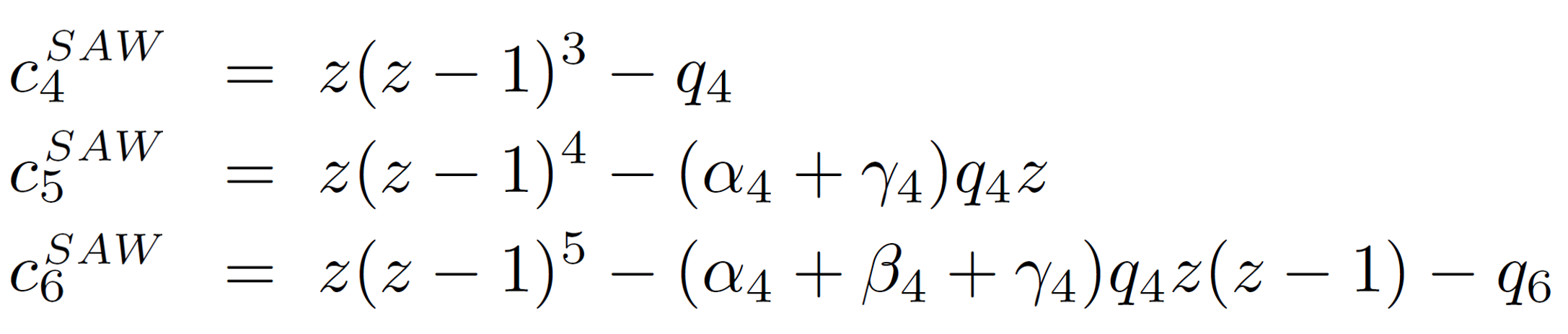
where q4 = 24, and q6 = 360.16 For the simple cubic lattice, the calculated numbers of loop-erased walks (LEW) of length N = 4, 5, and 6 are c4 = 726, c5 = 3534 and c6 = 16926, which are identical with the numbers of SAWs. For walks of seven and more steps, the method gives only the approximate number of SAWs, since we neglected loops of size s > 8 and also did not account for clusters of loops that share one or more steps (see figure below).

 

Exaples of (4-4)- and (4-6)-Loop Clusters

For example, for N = 7 the number of loop-erased walks is 81174 (81126 with the approxiate loop insertion probabilities) whereas the true value is c7 = 81390. If loop clusters are included in the sum both numbers are identical:

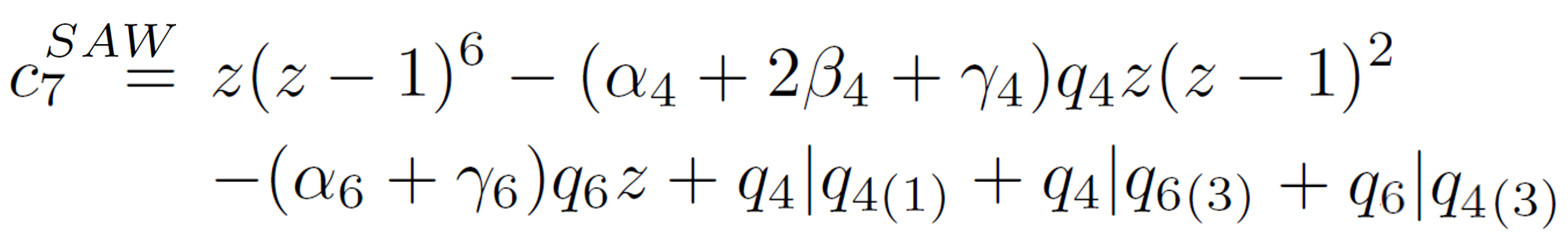
where qs|qt(i) is the number of consecutive loop walks of s and t steps when both loops share i steps, q4|q4(1)= q4|q6(3)= q6|q4(3) = 72. More results are plotted in the figure above, which shows the ratio PN = cN / [z (z-1)N-1] and the connective constant ⟨μ(N)〉 = N√cN for self-avoiding walks (○) and loop-erased walks (□) on a simple cubic lattice as a function of the number of steps N. The values of PNSAW for walks of up to 26 steps are taken from MacDonald et al.8 Except for walks of N = 9 - 12 steps, the deviation of cNLEW from cNSAW is less than 1% for all non-reversal walks of N < 20. These errors are surprisingly small given that only loops of up to 8 steps have been erased and clusters of loops have been completely neglected. One would expect that the number of loop erased walks, cNLEW, is always larger than the number of self-avoiding walks cNSAW since we did not erase all loop forming walks (smax < N ). This, however, is not the case for all values of cNLEW. One has to keep in mind, that all figure-eights of type (c) and all loops with more than eight steps have been neglected throughout the preceding treatment. The errors caused by these simplifications are of opposite sign, which could be the reason why cNLEW deviates very little from cNSAW. The accuracy of the calculation can be further increased when some simple clusters such as figure eights (c) and loops of 10 and 12 steps or so are erased as well. Since both large clusters and large loops have a very low probability of occurrence, cNLEW will deviate very little from cNSAW.

References & Notes

  1. M. E. Fisher, M. F. Sykes, Phys. Rev., 114, 45 (1959)

  2. M.F. Sykes, J. Math. Phys., 2, 52 (1961)

  3. M. Lautout-Magat, Macromolecules, 10, 1375 (1977) & 12, 715 (1979)

  4. M.F. Sykes, A.J. Guttmann, M.G. Watts and P.D. Roberts, J. Phys. A: Gen. Phys., 5 (1972)

  5. A.J. Guttmann and J. Wang, J. Phys. A: Math. Gen., 24, 3107 (1991)

  6. I. Jensen, J. Phys. A: Math. Gen., 37 5503 (2004)

  7. A. R. Conway, I.G. Enting and A.J. Guttmann, J. Phys. A: Math. Gen., 26, 1519 (1993)

  8. D. MacDonald, S. Joseph, D. L. Hunter, L. L. Moseley, N. Jan and A. J. Guttmann, J. Phys. A: Math. Gen., 33, 5973 (2000)

  9. K. Binder, Monte Carlo and Molecular Dynamics Simulations in Polymer Science, Oxford University Press 1995

  10. C. Domb and M.F. Sykes, Phil. Mag., 2, 733 (1957)

  11. G. Polya, R.E. Tarjan, and D.R. Woods, Notes on Introductory Combinatorics, Birkaeuser, Boston 1983

  12. K.Y. Lin and M. Chen, J. Phys. A: Math. Gen., 35, 1501-1508 (2002)

  13. Loops of s ≥ 8 steps form inner loops such as (d), (e) and (f). These walks will be counted multiple times unless the loops are quasi-self-avoiding, i.e. they do not form inner loops.

  14. αs needs to be omitted if N = s since there are no preceding steps.

  15. The probability for successful insertion of a loop of type (a) or (b) and size s in-between two steps (βs) and the respective probabilities for insertion of this loop at the beginning or at the end of a walk (αs, γs) can be calculated from:

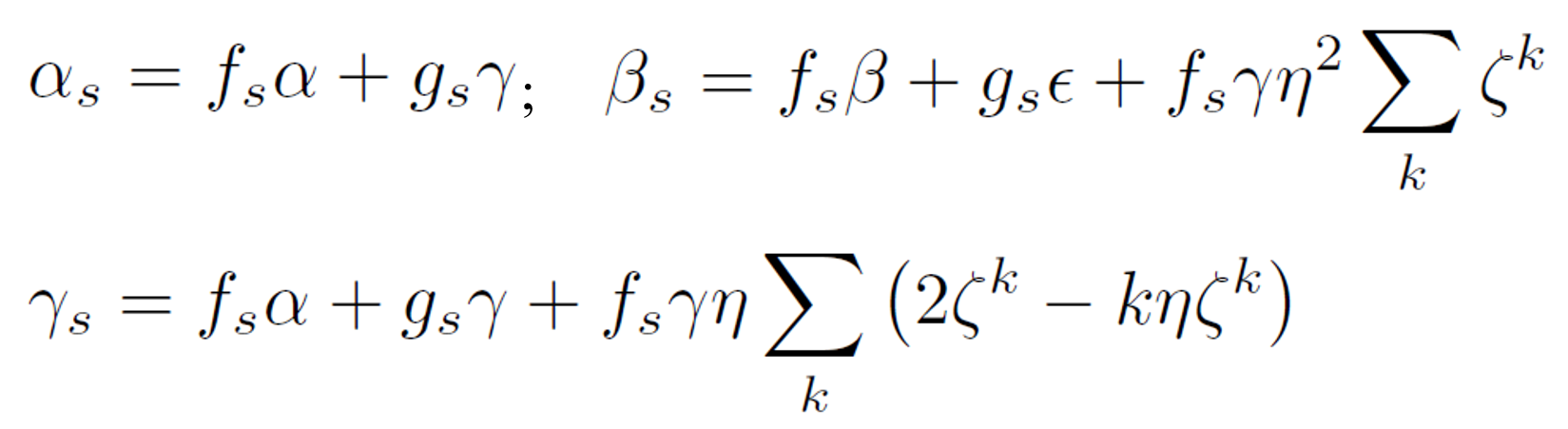
    where

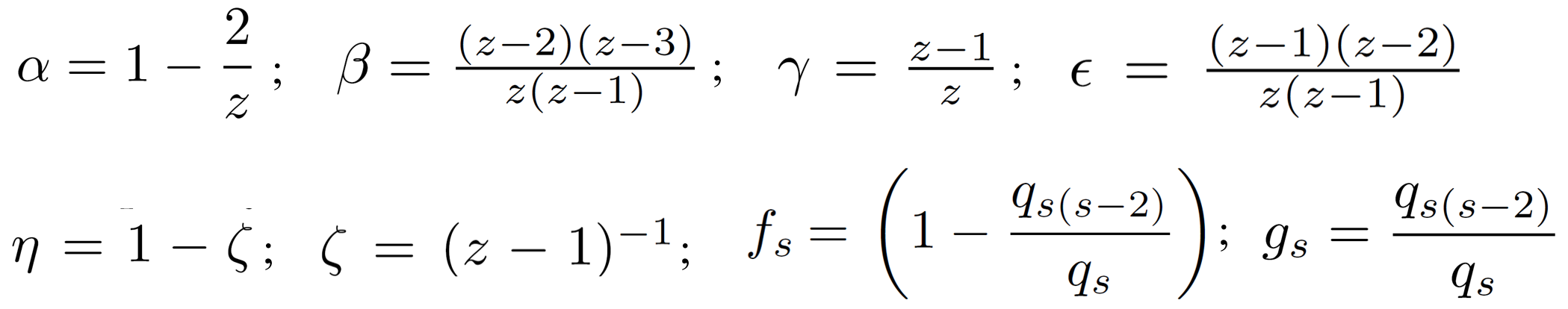
  16. For s ≥ 8, a loop may return several times to the vertex of insertion (d) or may form inner loops (e,f). To minimize the error of the calculation, the inserted loops must be quasi-self-avoiding in the sense that only the last and first step (or a sequence thereof) may overlap.

June 3, 2019; Revised July 8, 2019

  • Summary

    Self-avoiding Walk

    on a regular lattice is a sequence of vertices that are all unique. In other word, a self-avoiding walk (SAW) is a connected path which has no self-intersections (loops).

  • A SAW on a simple cubic lattice (Flory lattice) can be used to describe the (idealized) behavior of polymeric chains in an athermal solvent, i.e. to predict the static and dynamic properties of polymer chains.

  • Self-avoiding walks are very difficult to calculate and enumeration methods are very time consuming. Consequently, only a few results are known for relative short walks, as compared to random walks.

  • The computational time for the exact enumeration of the number of self-avoiding walks (cNSAW) on an unrestricted lattice is believed to grow exponentially as the number of steps increases.

  • The exact or approximate number of cNSAW on a lattice can be calculated by a simple application of the inclusion-exclusion principle from combinatorics.

  • The exact calculation of cNSAW is possible if we know the cumulative probabilities that a random walk forms at least one loop of size n = 2i + 2 but no loops of size n ≤ 2i for all n ≤ N.

  • In a random (lattice) walk, small loops are always much more abundant than large loops. Thus, in a first approximation, cNSAW can be estimated by exclusion of all walks that form small loops.

 Table of CNSAW