Reptation and Tube Model
The theory of reptation was first proposed by Piere Gill deGennes in 1971 and later extended to the tube model by Maasai Doi and Sam Edwards. This model describes the thermal motion of long polymer chains in concentrated solutions and melts. Doi and Edwards postulated that the motion of an entangled polymer molecule resembles the motion of a polymer in a tube, that is, they assumed that the long range motion of a polymer molecule is only allowed essentially along its own pass. Since the diffusion path resembles a wiggling snake deGennes termed the movement reptation which is the latin word for creeping. It is also the root for reptile.
The virtual tube is formed by the surrounding and entwining polymer molecules. Although each molecule is constantly moving, the virtual tube stays about the same for the entire time it takes the molecules to pass through it. This time is known as the relaxation time, τrep. Furthermore, the movement of the confined chains along the contour of the tube is not affected by the surrounding molecules. Thus, the tube model is based on two assumptions: (a) the movement of each molecule is independent of those of neighboring molecules, meaning no cooperate motion of polymer molecules takes place and (b) the lateral motion of the molecules can be neglected, that is, the molecules stay entirely within the virtual tube formed by the surrounding chains.
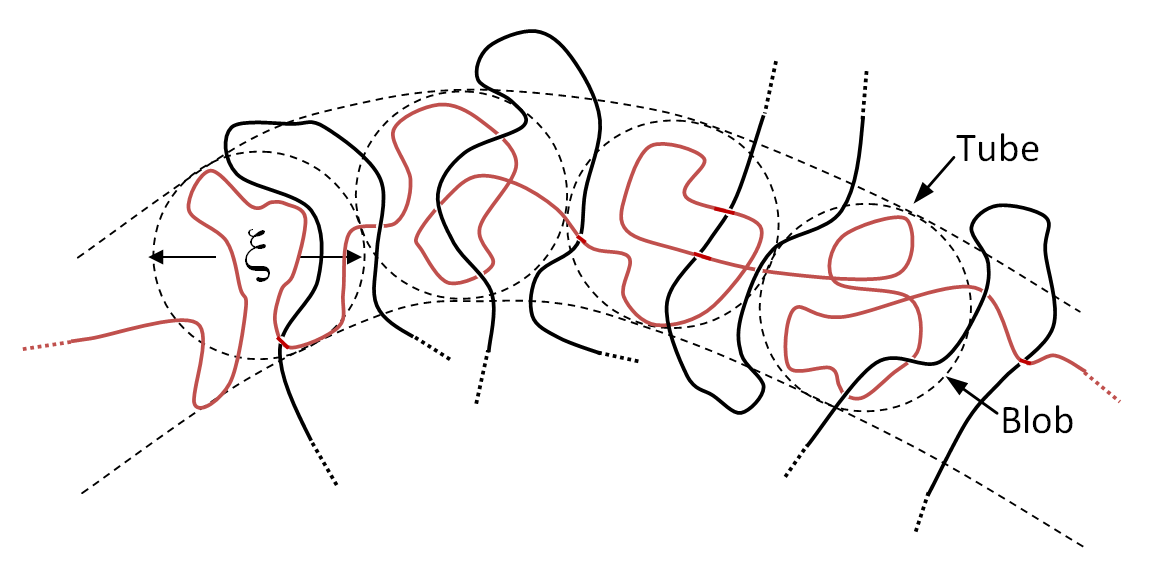
The primitive path describes the shortest path between the end groups of the polymer chain which coincides with the average positions of the monomers along the tube. It is seen from the figure above that this path constitutes the trajectory of a hypothetical chain of thickness ξ. To simplify the calculations, we replace the real chain with a Kuhn chain that consists of N statistical segments of length a. We further assume that the chain forms "blobs" of diameter ξ. Both the actual Kuhn chain of contour length, N a, and the primitive path, L, can be treated as random coils in the melt. Thus the contour length of the primitive path equals the number of blobs N / Ne times its average diameter ξ:
L ∼ N ξ / Ne ∼ N a / Ne1/2
where Ne is assumed to be equal to the number of segments between two successive entanglements, and ξ is equal to the average end-to-end distance of the subchain, ξ ∼ a Ne1/2.
The relaxation or disentanglement time corresponds to the time the chain requires to creep (diffuse) out of the inital tube. As will be shown below, this time is proportional to N3. Assuming random (Brownian) motion the mean squared displacement is given by
L2 ∼ Dt τ
Where Dt is the diffusion coefficient which can be calculated with the Einstein relation
Dt = kT / μt
and μt is the coefficient of friction of the chain creeping along the tube. This coefficient is N times higher than that of an individual link, μt = N μ. The time necessary for the Kuhn chain to displace the length of its original tube is then
τ ∼ L2 / Dt = L2 μt / kT = L2 N μ / kT
Recalling that L ∼ N a / Ne1/2 we obtain
τ ∼ a2N3 μ / Ne T ∼ N3 μ
Since the relaxation time determines the viscosity (η), the reptation model predicts
η ∼ N3 ∼ M3
where M is the molecular weight of
the polymer chain. This finding is in good agreement with the
experimental result, τ ∼ η ∼ M3.4.
Since the reptation model describes the motion of chains through
entanglements, it is only valid for long chains. In practice, this model is only applicable to polymers with
M >> Me. For shorter (unentangled)
chains, the viscosity is linear proportional to the molecular weight:
η ∼ N ∼ M
Thus, according to the reptation model, the transition from non-entangled to entangled polymer melt leads to a change in the power law exponent from ν = 1 to ν = 3.
References
P. G. De Gennes, J. Chem. Phys. 55, 572 (1971).
P.G. DeGennes, Scaling Concepts in Polymer Physics, Cornell University Press, New York, 1979
M. Doi, S.F. Edwards, The Theory of Polymer Dynamics, Oxford University Press, New York 1986
M. Rubinstein and R. Colby, Polymer Physics, 1st Ed., Oxford University Press (2003)