Rotational Isomeric State Model
Part 1: independent bond rotations

In the so called rotational isomeric state approximation, each molecule is treated as if it exists only in discrete torsional states corresponding to the potential energy minima of the rotational configuations. A simple example is given for n-pentane in the Figure below. Each of the inner bonds of the n-pentane molecule exist in three different states: the trans state (φ = +180°), the gauche+ state (φ = +60°) and the gauche- state (φ = -60°), termed t, g⁺ and g^-. By combining these three states, we get nine different rotational isomers tt, tg⁺, tg^-, g⁺t, g^-t,  g⁺g⁺, g^-g^-, g⁺g^- and g^-g⁺. Because of the symmetry in the molecular structure some of these states are equivalent: tg⁺ ≈ tg^- ≈ g⁺t ≈ g^-t and g⁺g⁺ ≈ g^-g^-.

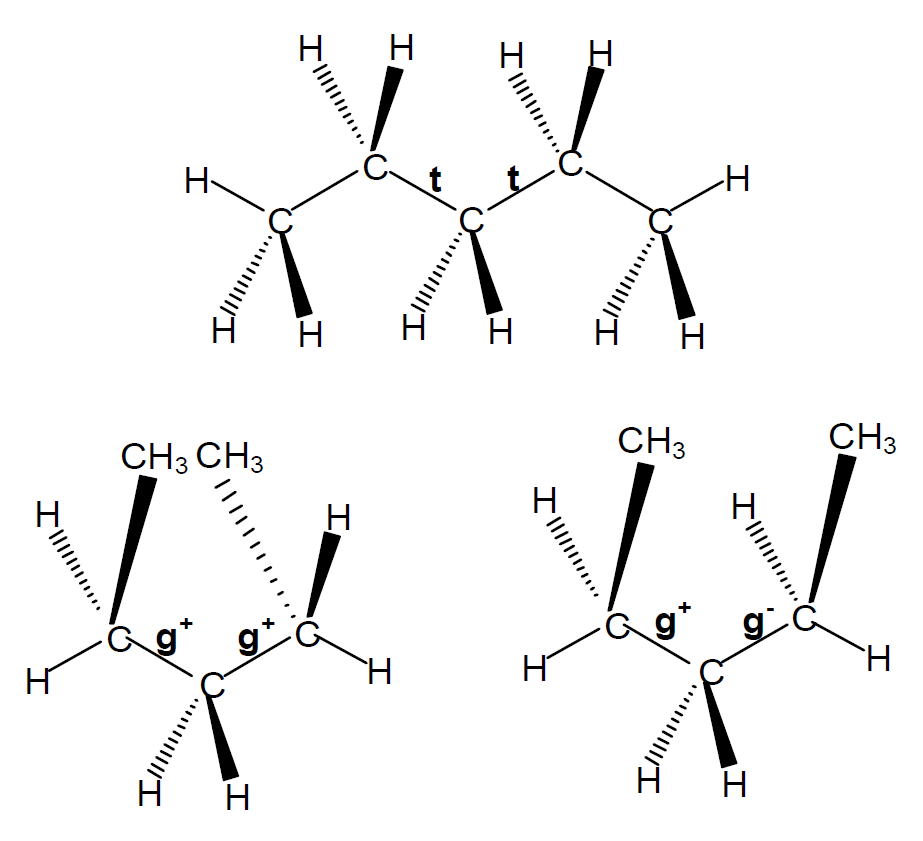
For the trans-trans-arrangement (t,t) the angles are φ₂ = φ₃ = 0°, for g⁺g⁺ φ₂ = φ₃ = 120° and for g⁺g⁺ φ₂ = -φ₃ = 120°. An exact treatment of the physical properties of a large polymer is very challenging. This is why scientist often use discrete states .

The rotational isomeric state approximation (RIS) for polymers was first introduced by Flory and Volkenstein. Their models ignore any variations around the local minima of the rotational state. As has been shown by them this assumption stil leads to the correct overall distribution of the end-to-end vector and thus, to the correct characteristic ratio. Before describing this model in more detail, we first explore the rotational isomeric states of a simple n-butane molecule. There are only three possible rotational isomeric states: t, g⁺ and g^-. The probability of occurance of one of these conformations i characterized by an angle φ_i, is given by a Boltzman factor:

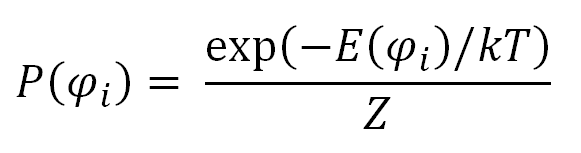
where Z is a normalizing factor called the partition function. It is the sum of the Boltzman energy factors for all possible angles:

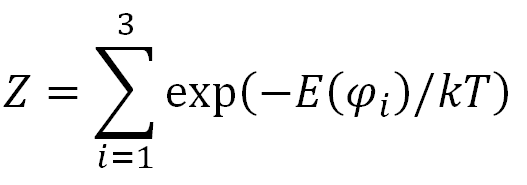
The three energy states of a butane molecule are E_g⁺, E_g^- and E_t. Then the partition function Z reads

where E_t = 0 has been chosen as the reference point. Knowing the partition function, other properties can be easily predicted. For example, the free energy and entropy per molecule are given by

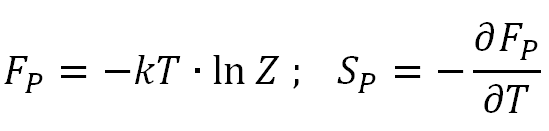
It is tempting to extend the equations above to polymer chains. If each polymer chain has N - 2 bonds (N = number of monomers), then the number of conformations per chain is ν^N-2 , where ν is the number of (discrete) rotational states. The partition function Z is given by

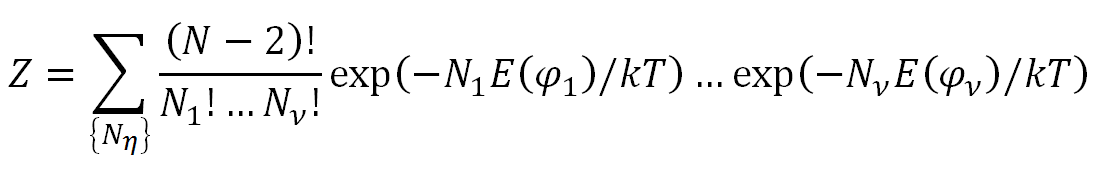
Using this partition function, the average value of the rotational angle becomes

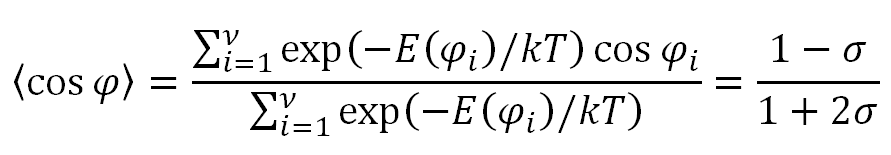
For very long chains, the characteristic ratio is

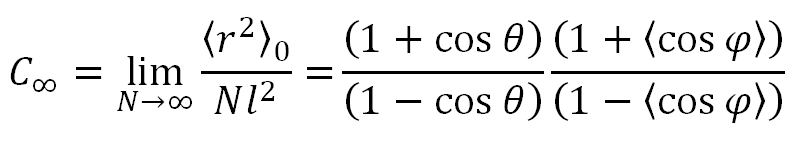
Using the widely accepted values E_g(140°C) = 2100 J/mol and θ = 68°, we find from the equations above C_∞ ≈ 3.6. The experimental value for polyethylene is C_∞ ≈ 6.7, thus much larger. One reason for this discrepancy is the erroneous assumption that the potentials for internal bond rotations are independent. However, monomers in a polymer chain that are separated by four bonds can be in close proximity when assuming gauche states which results in strong steric hindrance known as the pentane effect. It causes the energies of g⁺g^- or g^-g⁺ conformations to be much higher than those of g⁺g⁺ or g^-g^-. A model that includes these effects was developed by Flory and Volkenstein.^1,2 They used a generator matrix technique, which was invented a decade earlier. RIS models became very popular in the 1960s. A good overview of these models is given in Flory's classic book on rotational isomeric state theory.¹

References

1. P.J. Flory, Statistical Mechanics of Chain Molecules, Wiley, New York (1969)
2. M.V. Volkenstein, Molecular Biophysics, Academic Press, New York 1977