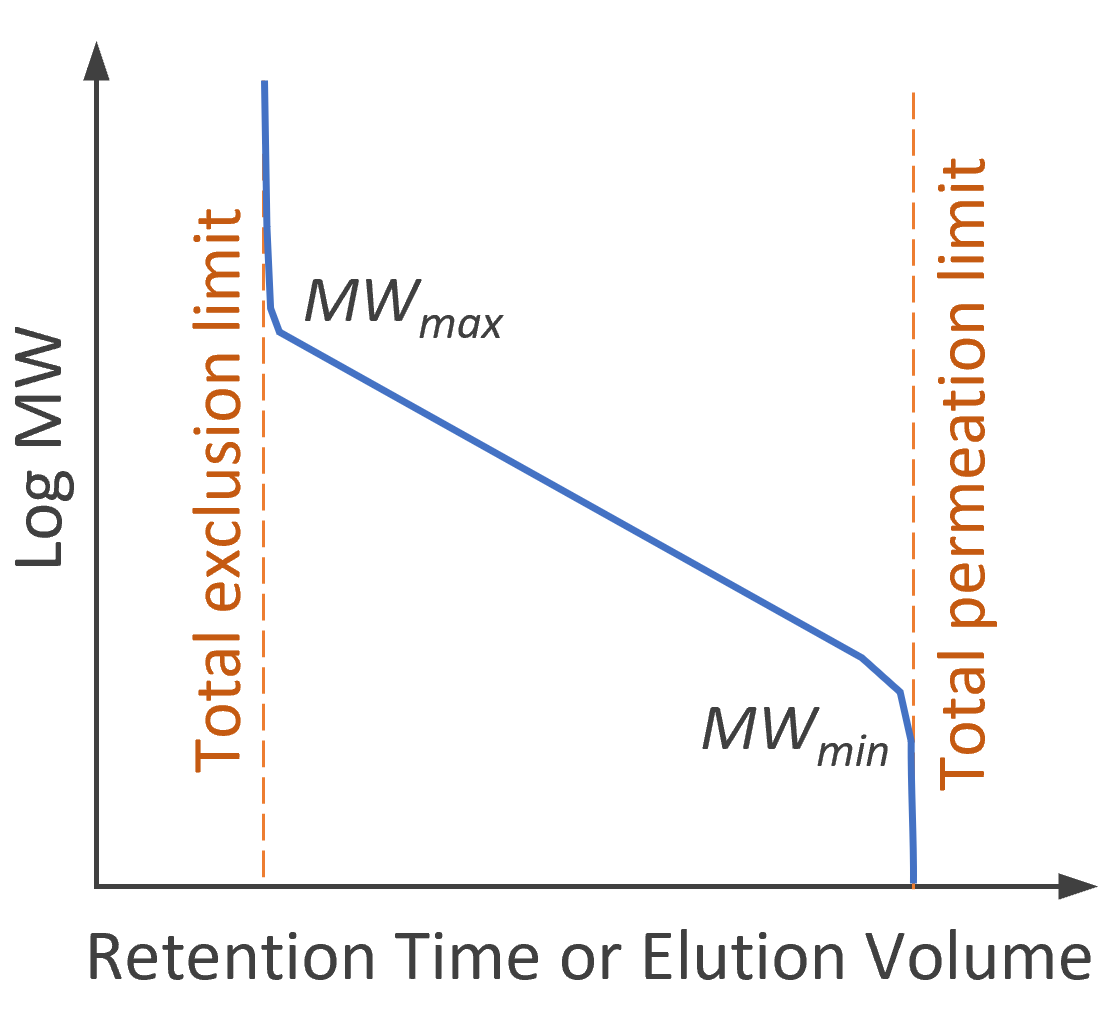
Thermodynamics of Size Exclusion Chromatography

The thermodynamics and the separation mechanism of SEC was first treated by Casassa, Gidding, Doi and Yau et al.^1-9 Their treatments are based on the assumption that the solute molecules continuously move between the stationary phase (pore volume) and mobile phase (interstitial volume) and assume a dynamic equilibrium throughout the separation column. A thermodynamic equilibrium is reached when the chemical potential of the macromolecules in both phases become equal. At low concentrations, the polymer solutionis ideal. Then the chemical potential of the macromolecules in the mobile phase of concentration (c_M) is given by

μ_M = μ_M,0 + kT · ln(c_M / c_M,0)

where μ_M,0 is the chemical potential of macromolecules in the reference state of concentration c_M,0.

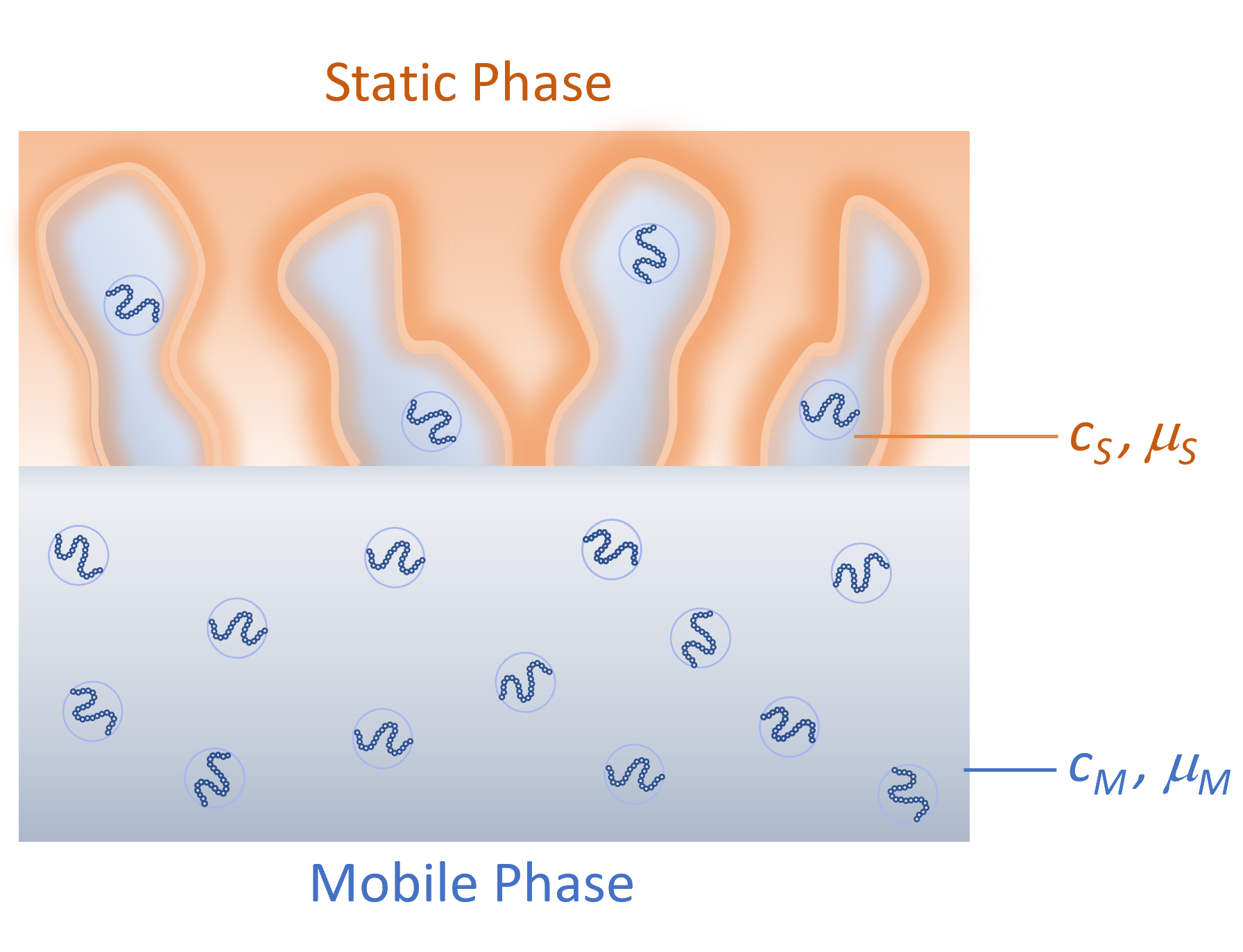
When a molecule diffuses into a pore (stationary phase) its entropy changes by ΔS and its enthalpy by ΔH. The change in entropy is caused by conformational and translational restrictions in the pores. In other words, a polymer squeezed into a pore can adopt a smaller number of conformations and the movement of the entire molecule is restricted by the pore walls. When a polymer enters a pore, surface–solvent contacts will be replaced by monomer–surface contacts, resulting in an enthalpy change. The change in enthalpy is due to interactions of the polymers with the pore surface. ΔH can be positive or negative depending on whether attractive or repulsive forces dominate. The chemical potential in the stationary phase (μ_S) of concentration (c_S) is then given by

μ_S = μ_S,0 + kT · ln(c_S / c_S,0) - TΔS + ΔH

The concentration equilibrium is reached when μ_S = μ_M. Then

kT · ln(c_S / c_S,0) - TΔS + ΔH = kT · ln(c_M / c_M,0)

Rearranging the terms gives the partition coefficient K = c_S/c_M^11,

K = exp(ΔS / k + ΔH / kT)

The enthalpic part ΔH is difficult to predict because it depends on the type of solvent, polymer and porous material. The entropic part ΔS, on the other hand, is universal because it is determined solely by the geometry and size of the pores and the hydrodynamic size of the polymer molecules. In an ideal SEC, the stationary phase has been designed to interact purely entropically with the eluent which requires a theta solvent and an inert porous packing. Then

K = exp(ΔS / k)

The separation effect of SEC also depends on the shape of the pores which are often of a highly convoluted complex shape. To understand the effect of pore size and pore geometry, several theoretical partition models have been developed that employ simple geometric equivalents of the polymers and the pore systems including (Gaussian) chains in slits, square tubes, cylinders as well as pores formed by randomly arranged spheres and randomly oriented planes.^3,9,13,14 One of the oldest models was developed by Cassasa who calculated the partition coefficient K of ideal polymers in pores from the Green function G(r, r') (also called segment distribution function). The simplest pore geometry is a slit-shaped pore formed by two parallel plates of width d extending in x and y directions. In the case of a Gaussian chain, the segment distribution function G(r, r') can be factored into three independent components G_x, G_y and G_z. The segment distribution parallel to the plates (G_x, G_y) will not be affected by the slit. In other words, only G_z experiences a change. As has been shown by Cassada and others, the Gaussian segment distribution for this type of confinement is given by^{1-3, a}

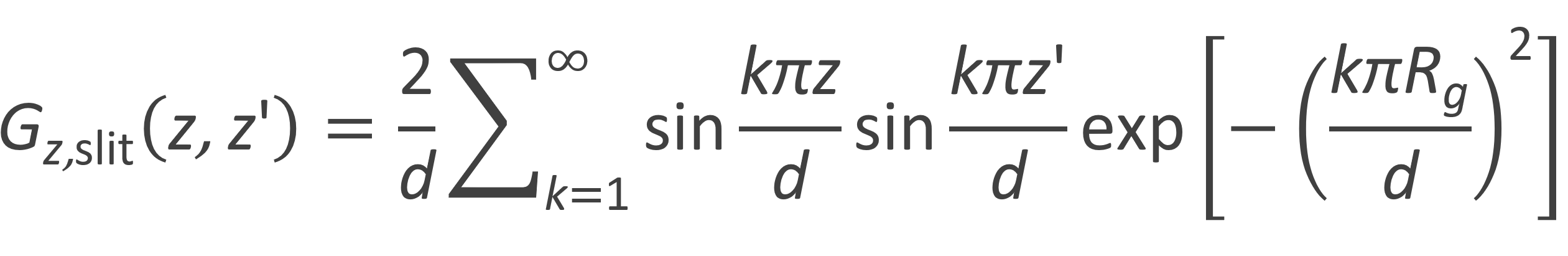
whereas the Gaussian probability distribution for an unperturbed chain is given by

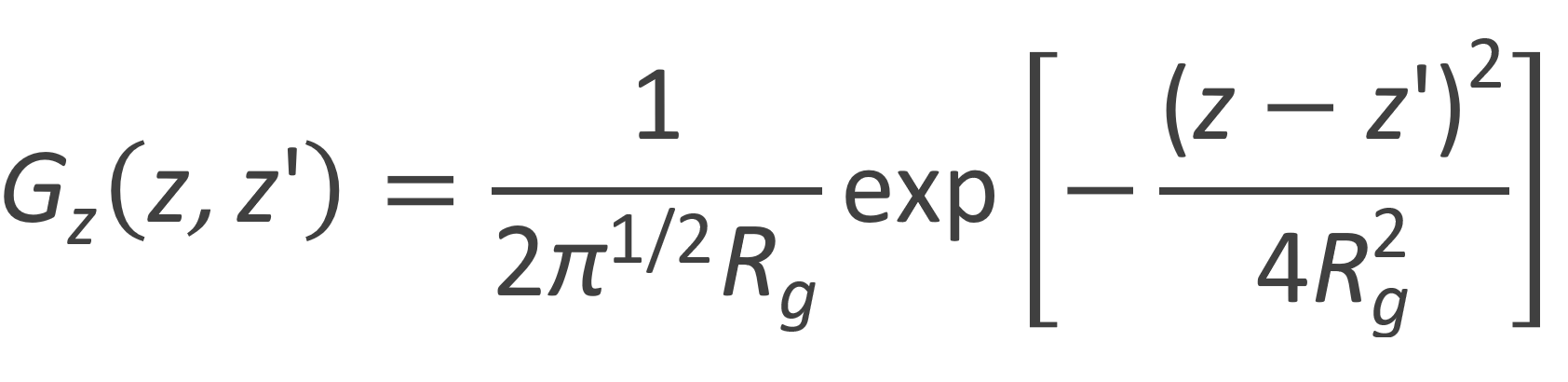
The partition coefficient of a polymer in a slit K_slit can be calculated as the average of the Green function with respect to z and z':¹⁰

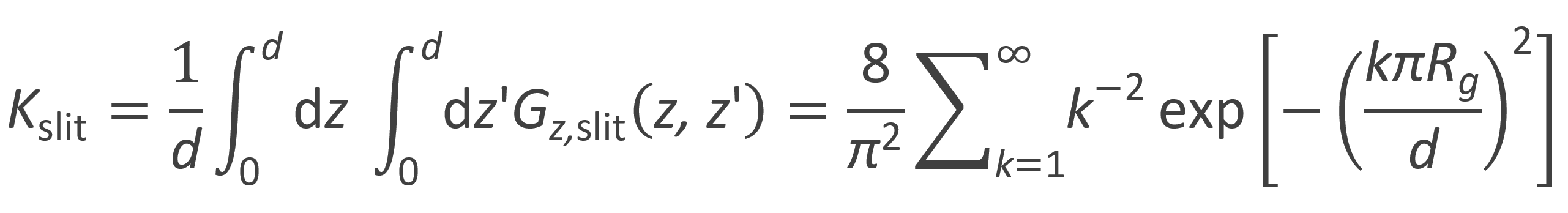
For narrow slits, R_g >> d, the first term dominates the series. Then

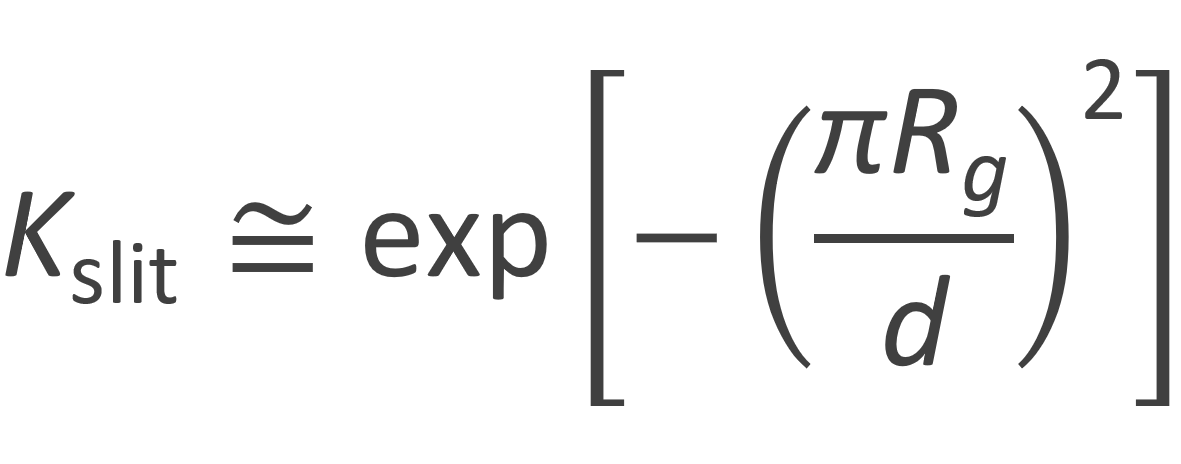
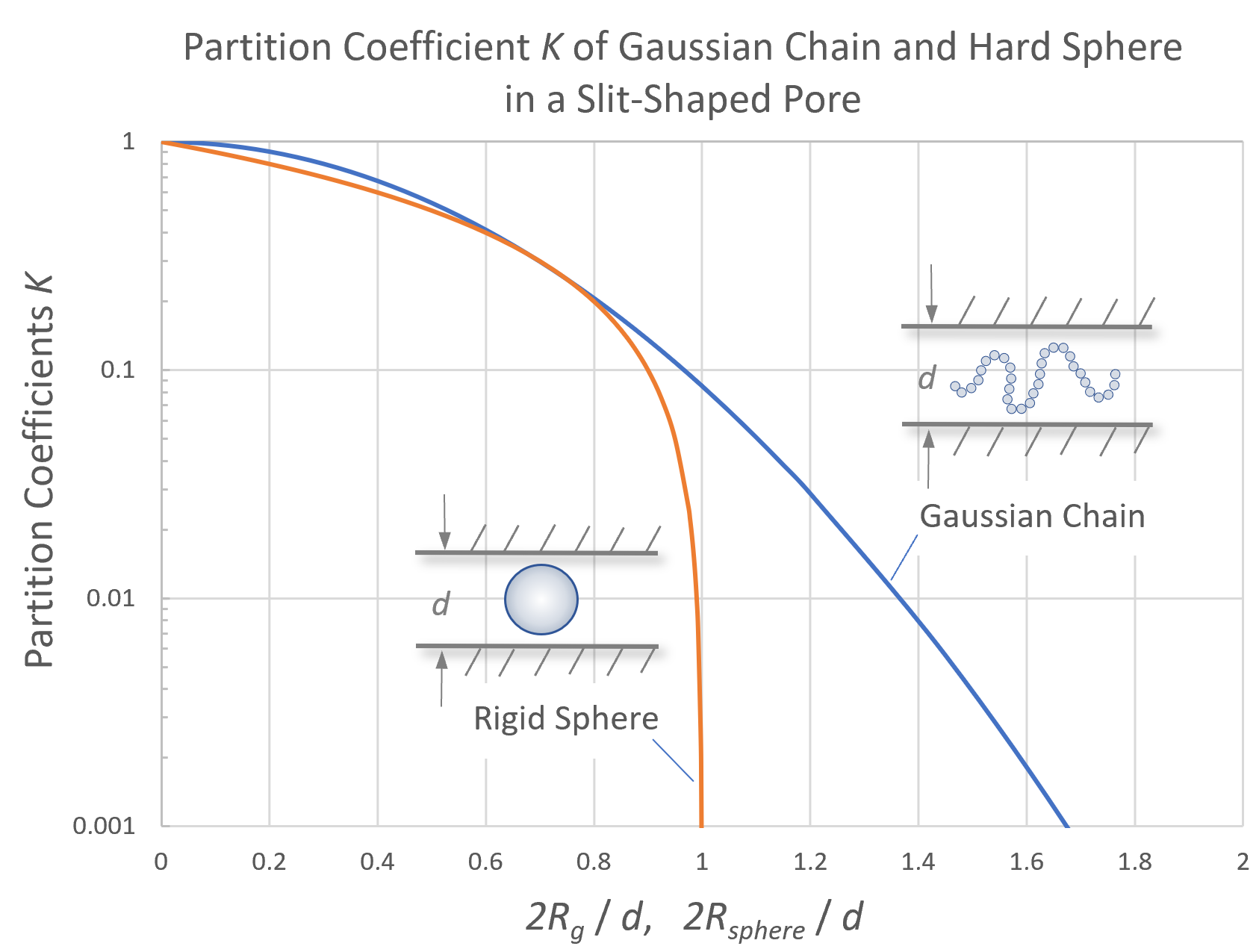
The figure below compares the partitioning coefficient of Gaussian chains with hard sphere molecules in slit-like pores of width d. The plot of K is given as a function of 2R_g/d. At 2R_g = d, the concentration in the pores is approximately 1/3 of the concentration in the mobile phase, whereas the concentration of hard spheres asymptotically approaches zero. For very large pores, (2R_g/d → 0), the partition coefficient K approaches unity for both hard spheres and flexible macromolecules. Then the molecule concentration inside the pores approaches asymptotically the concentration outside the pores (total permeation limit). Thus, the separation column becomes insensitive for polymers much smaller than the pores. If, on the other hand, the molecules are much larger than the pores, all macromolecules are excluded from the pores and the concentration inside the pores approaches zero (total exclusion limit). In other words, all molecules that pass through the column are eluted at approximately the same time t_M and no separation occurs.

A real polymer chain in a pore will behave very differently than an ideal chain (chain in a theta solvent) since it is more extended in a confined space. We therefore expect real chains to have very different partition coefficients than ideal chains. Unfortunately, an exact treatment of real polymers in confinement is not possible, that is, their partition coefficients even in simple confining geometries are unknown. As has been shown by Teraoka¹¹, it is possible, however, to obtain asymptotic expressions between ΔS and N for sufficiently long chains in simple geometrical confinement using scaling arguments.

Let us consider a real chain confined in a cylindrical pore of diameter d. If its radius of gyration (R_g ∼ N^3/5) is much smaller than the pore radius, the chain conformations are not much affected by the tube walls. However, when R_g exceeds the pore radius, the chain in the tube is forced to adopt conformations that are extended in the direction of the cylinder. As has been shown by Teraoka¹¹, Rubinstein¹⁸ and others, a chain confined in a tube can be envisioned as a train of blobs of diameter ξ = d along the pore channel (see figure below).

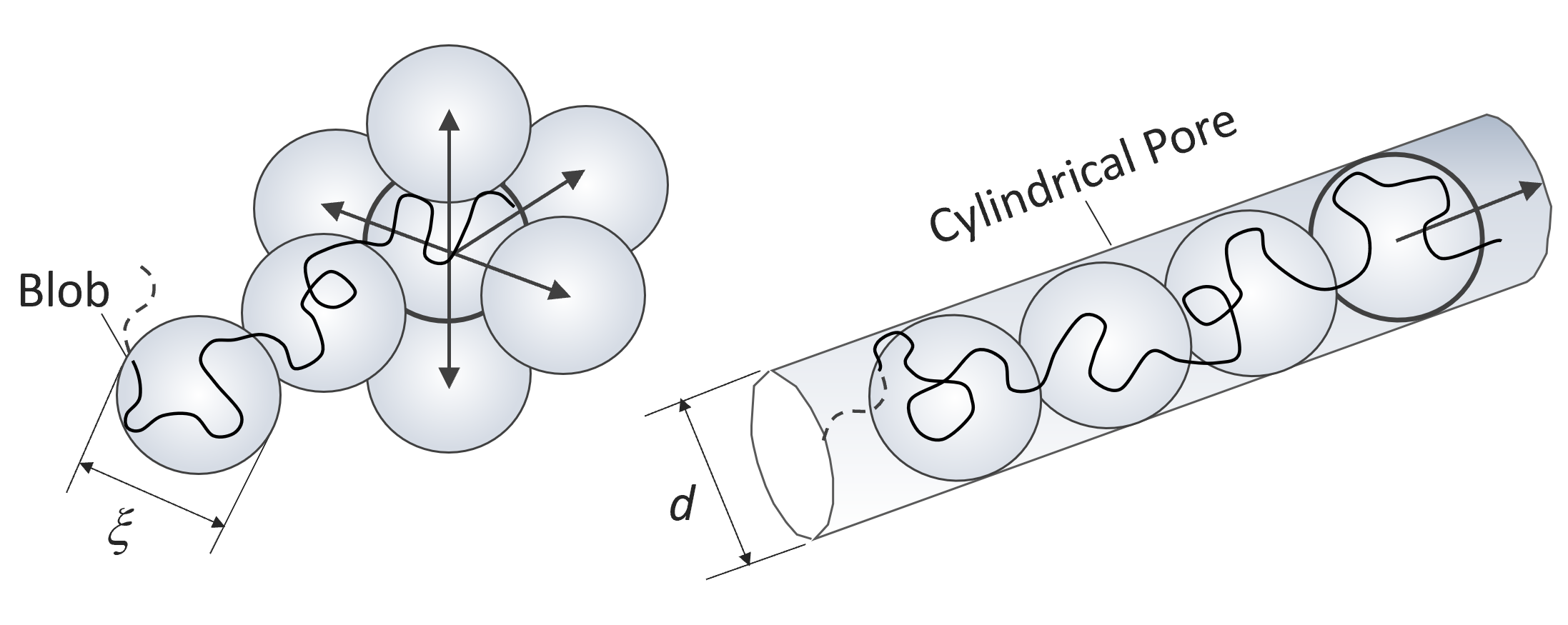
Each of the partial chains within each blob assumes a conformation of a real chain in the absence of confinement. Then the size of the subchain follows the same scaling laws as those in unconfined space:

ξ ≅ b g^3/5

where b is the length of a statistical segment and g is the number of segments in a blob. The polymer chain consists of n_d = N/g blobs each having the same size d. Assuming a simple cubic lattice and placing the spherical blobs on the grid points, each neighboring blob of the sequence of self-avoiding spheres can be placed on any of the five adjacent grid points, whereas in the tube the blobs have only one choice. Then the n_d blobs in free space can be arranged in approximately 5^n_d different ways, whereas in the pore only one linear arrangement of blobs is possible. As has been shown above, the partition coefficient can be calculated as the exponent of the entropy, K = exp(S/k_B), which is identical to the ratio of all possible chain conformations in the mobile phase to those in the pore. Since the monomers inside a blob are unperturbed, the loss in entropy is solely due to restriction in blob mobility. Then K can be calculated as the number of arrangements of blobs outside the pore (mobile phase) to those inside the pore:¹¹

K ≅ 1/5^n_d

The change in entropy ΔS is given as

- ΔS/k = - lnK_pore ≅ n_d = N/g ≅ N (b/d)^5/3 ≅ (R_g/d)^5/3

or

K_pore ≅ exp[-(R_g/d)^5/3]

In the case of a slit shaped pore, the blobs are arranged in a two-dimensional way. Then a sequence of blob in a slit can be placed on an imaginary 2-dimensional cubic grid in 3^n_d different ways. Using the same relationships we find that

K ≅ (3/5)^n_d

The arrangement of blobs in a slit is equivalent to a two-dimensional self-avoiding walk. The length of such a walk scales as

R_|| ≅ d (N/g)^3/4 ≅ d (R_g/d)^5/4

where we made use of the scaling relationships g ≅ (d/b)^5/3/b and R_g ≅ b N^3/5. Similar scaling relationships can be derived for polymers in a θ-solvent; when ideal chains are squeezed into a cylindrical pore, the polymer blobs can assume more than one arrangement since neighboring blobs are allowed to overlap. Assuming a one-dimensional lattice, the number of arrangement of blobs in the pore is 2^n_d whereas in the free solution (mobile phase), the same blobs can be arranged in 6^n_d different ways. Then K = 1/3^n_d and The change in entropy ΔS is^11,13

- ΔS/k = - lnK_pore ≅ N/g ≅ N (b/d)² ≅ (R_g/d)²

References, Notes & Further Readings

1. E.F. Casassa, J. Polym. Sci. Part B: Polym. Lett. 5, 773 (1967)
2. E.F. Casassa and Y. Tagami, Macromolecules, 2, 14 (1969)
3. E.F. Casassa and Y. Tagami, J. Polym. Sci. Part A-2: Polym. Phys. 6, 63 (1968)
4. E.F. Casassa,d J. Polym. Chem. 75, 3929 (1971)
5. E.F. Casassa, Sep. Sci. 6, 305 (1971)
6. W.W. Yau, C.P. Malon, and S.W. Fleming, J. Polym. Sci. B, 6,803 (1968)
7. W.W. Yau., J. Polym. Sci. A27, 483 (1969)
8. M. Doi, Trans. Faraday Soc. I1,71, 1720 (1975)
9. J.C. Giddings et al., J. Phys. Chem. 72, 4397 (1968)
10. M. Doi, S.F. Edwards, The Theory of Polymer Dynamics, Oxford University Press, New York 198
11. I. Teraoka, Polymer Solutions: An Introduction to Physical Properties, John Wiley (2002)
12. H.G. Barth, Early Development of Size-Exclusion Chromatography, LCGC 31, 7, 550-558 (2013)
13. J.C. Day, B. Alince and A.A. Robertson, Can. J. Chem., 56, 2951-2958 (1978)
14. K.H. Altgelt and L. Segal, Gel Permeation Chromatography, Marcel Dekker, New York. NY. 1971
15. J.V. Dawkins, Pure & Appi. Chem. 54, 281 (1982)
16. N. Donkai, A. Nakazawa, H. Inagaki, Bull. Inst. Chem. Res. 48, 79, 1970
17. D. Berek, J. Sep. Sci. 33, 315 (2010)
18. M. Rubinstein and R. Colby, Polymer Physics, 1st Ed., Oxford University Press (2003)