Blob Model
The idea of polymer blobs was first introduced by Pincus in 1976.1 Pincus postulated that the repulsive interactions of a polymer coil in a good solvent are partially screened by the presence of other chains that entangle (overlap) with the polymer. Thus, a polymer in a concentrated solution is less expanded than in a dilute solution because when polymers start to overlap, the excluded volume interactions become partially screened.2 Then a blob represents the unit of chain length that is swollen, i.e., the average unit length that is not overlapping with other polymer chains nearby.
Blobs of size
ξ having
gN Monomers of Size
l
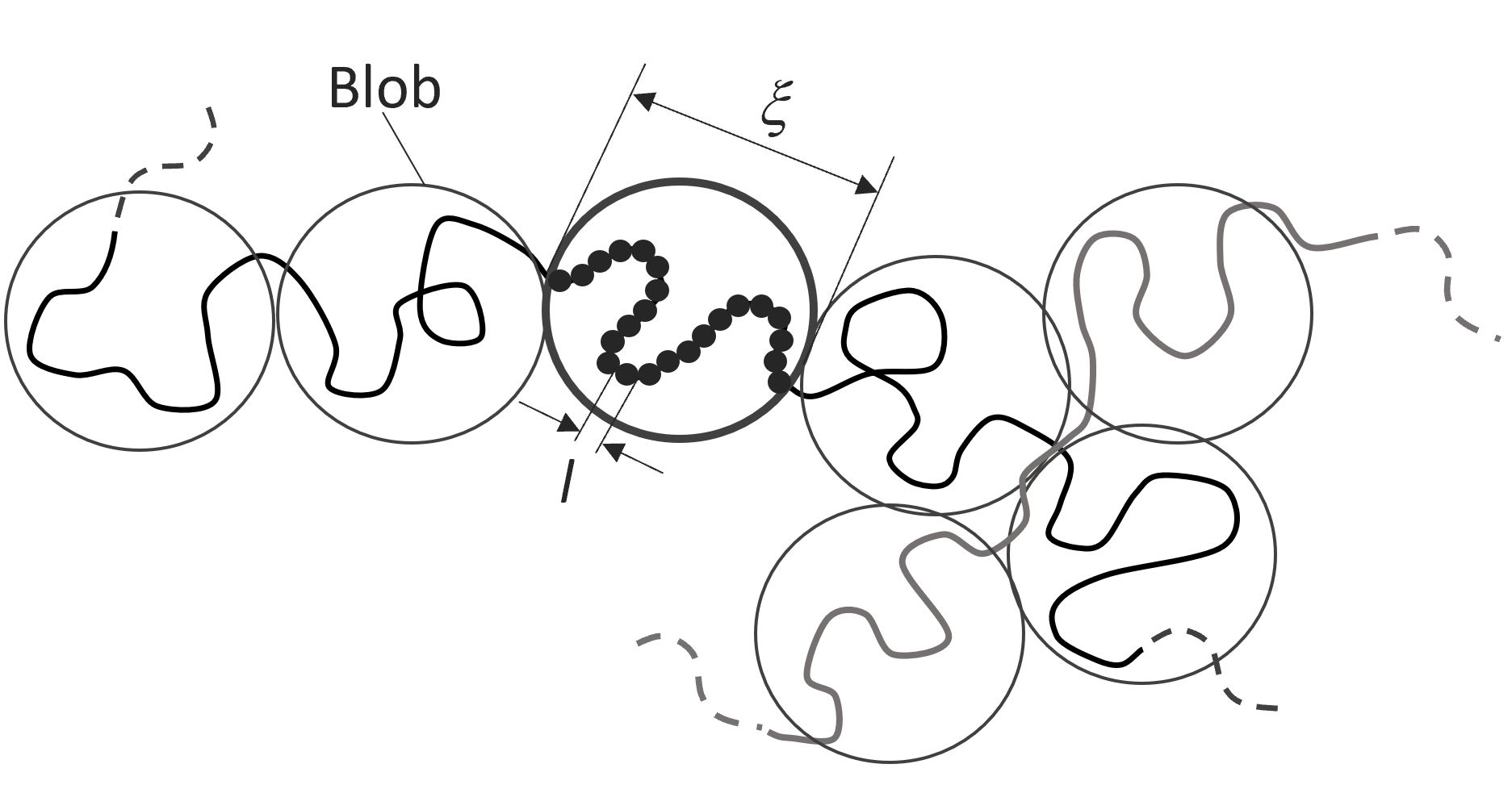
Blobs of size ξ having gN Monomers of Size l
The scaling behavior of blobs in concentrated solutions is inverse to that of random thermal coils, that is, on a large scale, polymer coils behave like Gaussian chains, and at a small scale (shorter distances), they display good solvent behavior. Then a polymer in a concentrated solution can be described by a sequence of N / gN blobs of size ξ, each containing gN monomers. The monomers inside these blobs display good solvent behavior (ν = 3/5), whereas the sequence of blobs shows ideal behavior:7
ξ ∼ l gN3/5 ,
R ∼ ξ (N / gN)1/2
Note, in the melt state, the behavior of polymers is entirely Gaussian. But as the polymer concentration is decreased, the polymer coils become swollen on short spatial distances and display good solvent behavior. As more solvent is added, the scale of good solvent behavior increases until the entire solution shows good solvent behavior. Thus, the size of a blob strongly depends on the polymer concentration; below the overlap concentration c < c* ∼ N / R3, the polymers can be considered isolated and the size of a blob ξ is identical with the Flory radius of the polymer, RF ∼ l N3/5. For c > c* the coils interpenetrate each other and the scale ξ is a function of concentration. These two requirements lead to following concentration dependence7:
ξ(c) ∼ RF f(c/c*) = RF (c/c*)mξ
where the correlation length ξ must be independent of the chain length N. Then the exponent mξ and the power of N from the Flory radius (RF ∼ N3/5) must cancel each other. This is the case for mξ = -3/4:6,7
ξ(c) ∼ l c-3/4
Note, this relationship is only applicable to the concentration regime c > c* whereas below the overlap concentration, the chains are isolated. Then the blob contains the entire chain.
In the semi-dilute to concentrated solution the blobs occupy the entire solution space, meaning the blobs are closely packed, c = gN / ξ3. From the scaling relation ξ ∼ l gN3/5 and the concentration dependence of blobs ξ(c) ∼ l c-3/4 it follows6,7
gN ∼ (ξ / l)5/3 = c-5/4
Using these two expression, the mean square end-to-end distance can be rewritten as4-7
RF2 ∼ ξ2N / gN = N l2 / c-1/4
This equation was first derived by Daoud and confirmed with reasonable accuracy by neutron scattering on polystyrene solutions.4
References, Notes & Further Readings
- P. Pincus, Macromolecules, Vol. 9, No. 3 (1976)
This behavior is very similar to charged polymers in a salt solution where the surrounding ions screen the repulsive coulomb interaction between charged chain segments.
We consider a polymer solution as concentrated when the polymer coils overlap. This is the case when
c* > N / R3 = N / (l Nν)3 = l3 N1-3νM. Daoud, et al., Macromolecules 8, 804 (1975)
- M. Doi, Introduction to Polymer Physics, Oxford Science Publications (1995)
- I. Teraoka, Polymer Solutions: An Introduction to Physical Properties, John Wiley (2002)
- P.G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press (1970)
- G. Strobl, The Physics of Polymers, 3rd Edition, Heidelberg 2007
- A. Y. Grosberg, A.R. Khokhlov, Statistical Physics of Macromolecules, AIP Press (1994)
- M. Rubinstein and R. Colby, Polymer Physics, 1st Ed., Oxford University Press (2003)