Blob Models of Stretched Polymer Chains in Solution
The blob model and the scaling theory are frequently employed to describe the thermodynamic behavior of isolated polymer chains and chains in semidilute solution. In the blob model a blob represents the average unit length that is not overlapping with other polymer chains nearby. Then a polymer chain can be described by a sequence of N / g blobs of size ξ, each containing g monomers. The monomers inside these blobs display good solvent behavior (ν = 3/5), whereas the sequence of blobs shows ideal behavior.
Stretched Chain consisting of N/g Blobs of size ξ
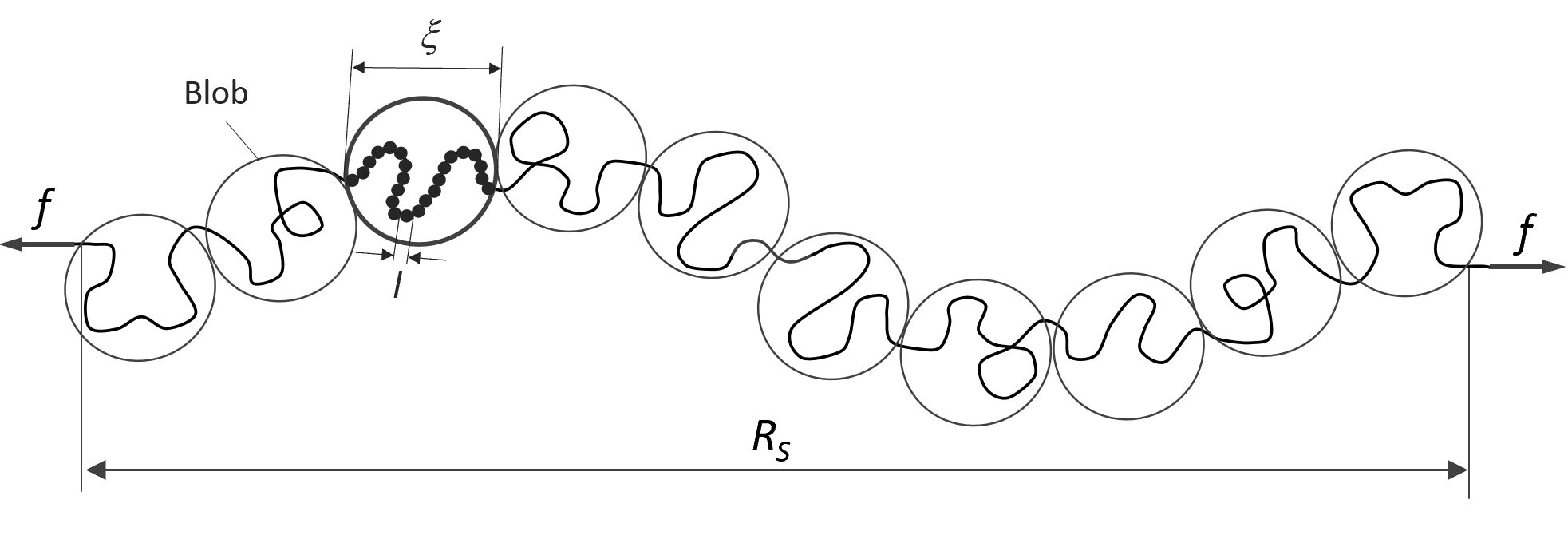
Stretched Chain consisting of N/g Blobs of size ξ
Let us first consider an isolated polymer chain in an athermal solvent with excluded volume vexcl ≈ l3. In the unperturbed state the end-to-end distance of such a chain is given by following simple scaling relation:
R0 ≈ l N3/5
It is assumed that both ideal and real chains in a solvent exhibit self-similarity, i.e., fractal behavior. Hence the scaling laws that apply to the entire chain also apply to subsections of the chain, i.e. to blobs:
ξ ≈ l g3/5
where the correlation length ξ must be independent of the number of segments N.
Polymer chains stretched by external forces can be envisioned as an array of tension blobs that are more or less aligned along the direction of deformation.
The end-to-end distance Rs of such a chain is simply the product of the tension blob size ξ and the number of blobs N/g:
Rs ≈ ξ N/g ≈ N3/5
Using ξ ≈ l g3/5 → g ≈ (ξ/l)5/3, Rs can be rewritten as:
Rs ≈ N l5/3 / ξ2/3 ≈ Rs5/3 / ξ2/3
The increase in free energy due to the restriction of the degrees of freedom of the blobs is of the order kT per tension blob (neglecting prefactors of order unity).1,2 Then the free energy is directly proportional to the number of blobs:
F(N, Rs) / kT ≈ N/g ≈ Rs /ξ ≈ (Rs /R0)5/2
The force required to stretch the polymer coil can be obtained by differentiation of the free energy with respect to the end-to-end distance:
f = δF(N, Rs) / δRs ≈ kT / ξ ≈ kT Rs3/2 / R05/2 ≈ kT/R0 · (Rs/R0)3/2
This non-linear relationship between the tension force and elongation was first derived by Pincus.3,4 For this reason, tension blobs are often called Pincus blobs.
The scaling relationships for expanend athermal polymer chains can be generalized to chains with any fractal dimension 1/ν, as has been shown by Colby and Rubinstein:4,5
F(N, Rs) / kT ≈ (Rs / lNν)1/(1-ν)
For example, the fractal dimension of a chain in a θ-solvent is ν = 1/2. Then the equation reduces to:
F(N, Rs) / kT ≈ (Rs2 / Nl2) ≈ (Rs /R0)2
Since chains in a good solvent have fewer possible conformations than chains in a θ-solvent, they will lose fewer conformations when stretched. Then the resulting free energy cost for stretching will be also lower.
References, Notes & Further Readings
Since a blob is defined as the length scale over which the elastic energy is of order kT, a polymer stretched by an external force will be unperturbed on length scales smaller than the blob size, ξ.
Calculation based on renormalization group methods and measurements give a more accurate value of ν = 0.588. Then the free energy per tension blob reads
F(N, Rs) / kT ≈ (Rs /R0)2.4- P. Pincus, Macromolecules, Vol. 9, No. 3 (1976)
- M. Rubinstein and R. Colby, Polymer Physics, 1st Ed., Oxford University Press (2003)
- The scaling relations above are not applicable to large extensions near maximal elongation.
- M. Doi, Introduction to Polymer Physics, Oxford Science Publications (1995)
- I. Teraoka, Polymer Solutions: An Introduction to Physical Properties, John Wiley (2002)
- P.G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press (1970)
- A. Y. Grosberg, A.R. Khokhlov, Statistical Physics of Macromolecules, AIP Press (1994)