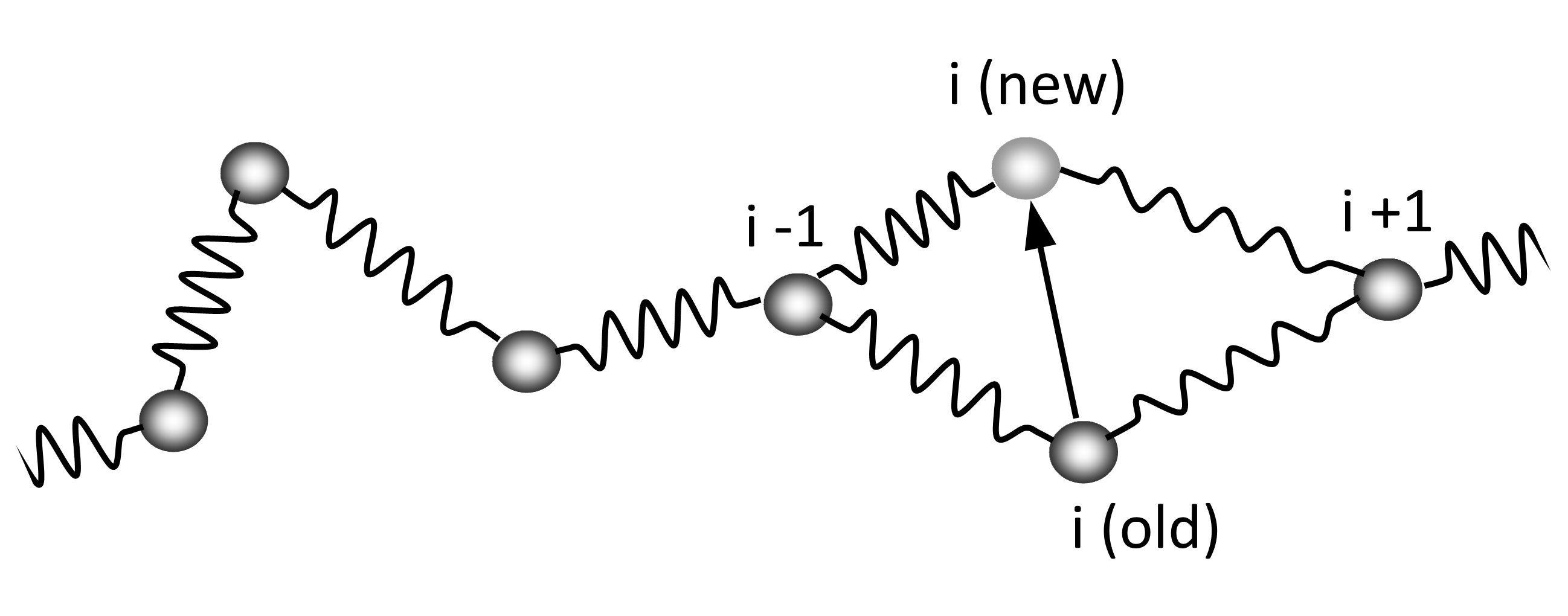
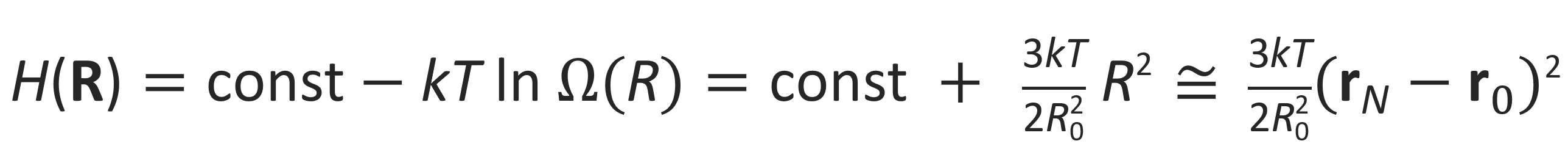Bead-spring Model and Gaussian Chains

One of the most popular polymer models is the so called bead-spring model. In this model, the high-molecular weight polymer is described as N + 1 beads conneceted by N massless (harmonic) springs (see Figure below). Each bead may represent a subchain that contains several repeat units. In many cases, a simple harmonic potential is assumed, that is, the virtual springs follow Hooke's law of elasticity, which implies they are infinitley extendable with a linear elastic response. The potential energy of such a chain can be calculated from the positions of each bead in space, r_i, or from the relative distance between the beads, l_i:

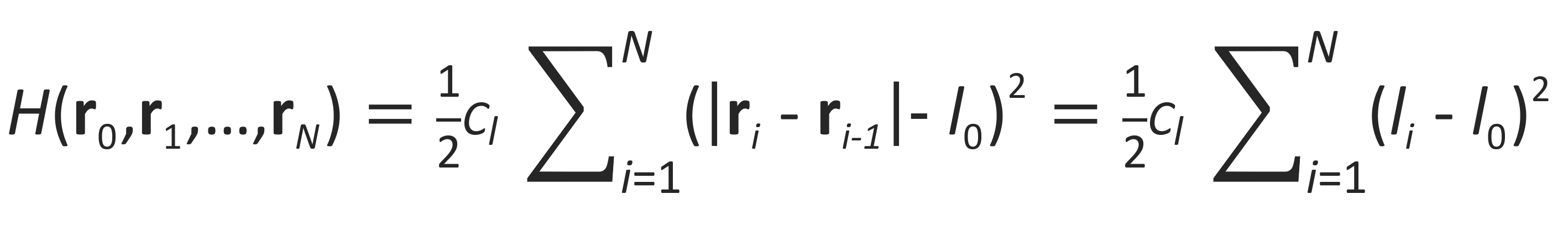
where one typically choses the constants C_l,, l₀ and l_max in relation to the parameters ε, σ of the Leennard-Jones potential between the effective beads (if one allows only finite extension of the beads).

In viscous media (polymer melts), the kinetic motion (energy) of the polymer chain can be neglected. Then, the Boltzmann distribution of a random arrangement of r₀,..., r_N is given by:

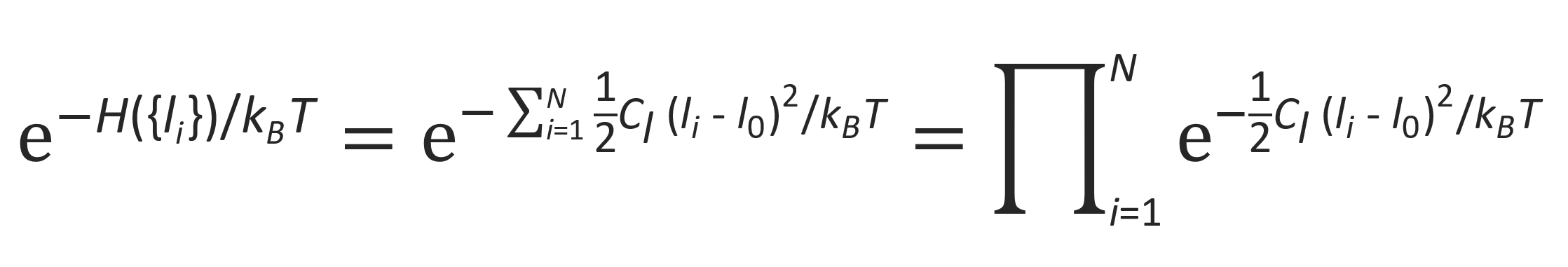
The simplest case is a Gaussian probably distribution of the beads, that is, it is assumed that the beads show ideal chain behavior. For this case, the spring constant reads

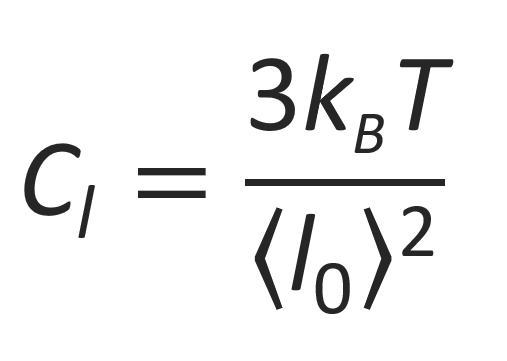
where ⟨l₀²⟩ is the mean squared end-to-end distance of two adjacent beads which is equal to the length of a spring in its relaxed state. With this force constant, the statistical weight for each conformation {r_i} can be rewritten to an expression that depends only on the extensions of the springs {l_i-l₀}:

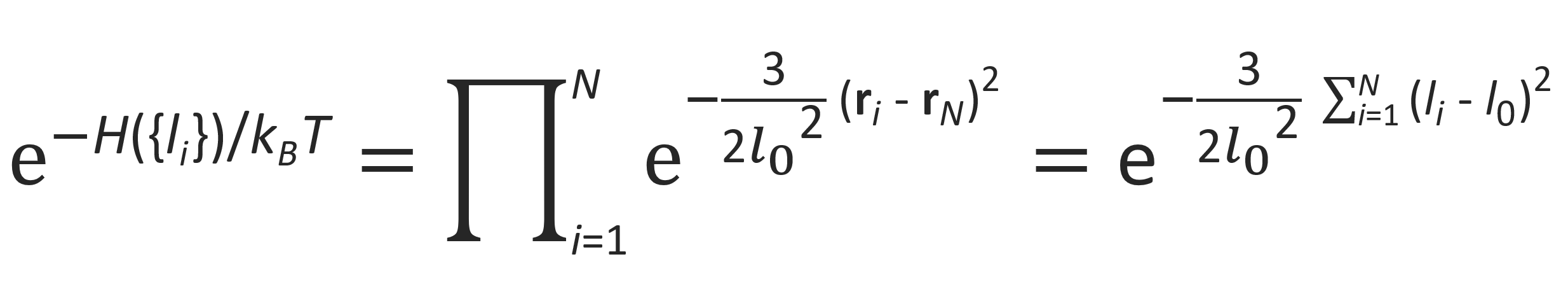
The two ends of the Gaussian chain behave like two beads connected by a single spring. Its force constant is given by

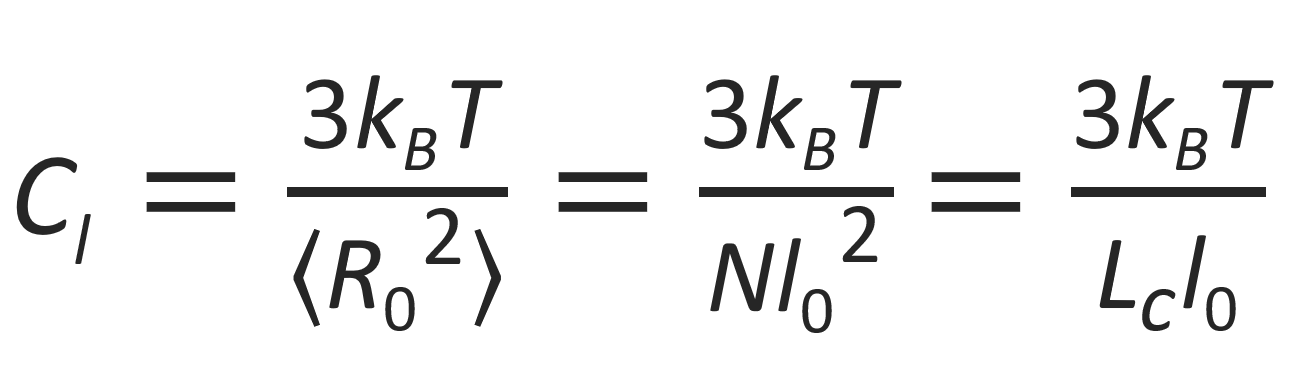
where ⟨R₀²⟩ = Nl₀² is the mean square end-to-end distance of the entire chain and L_c is the "contour length" of the chain, i.e. the end-to-end distance of the fully extended chain.² Then the Helmholtz free energy H of the chain can be written as⁴

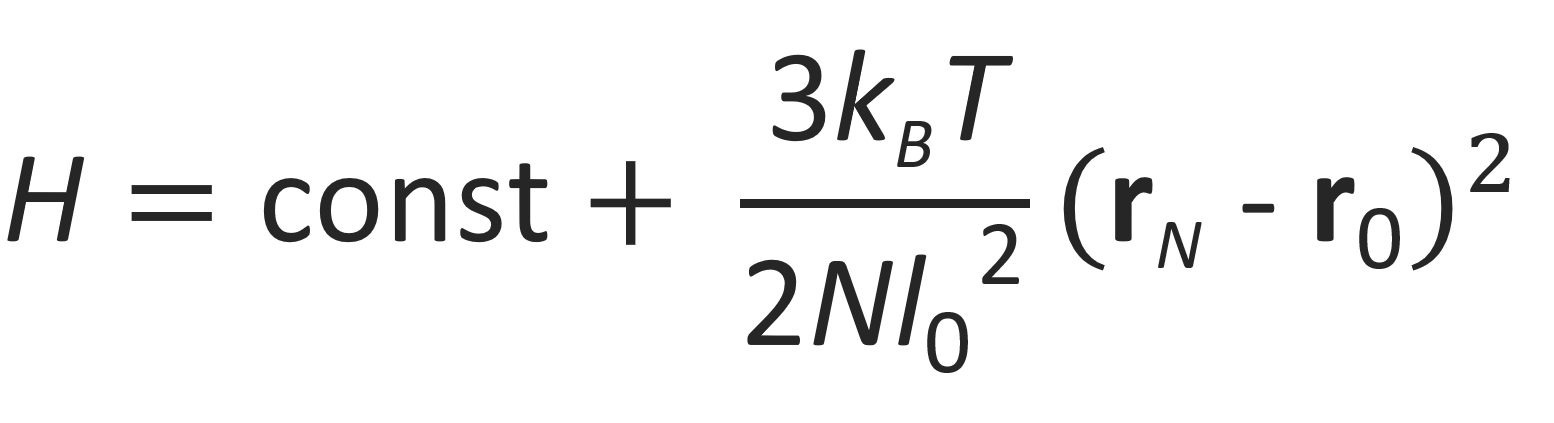
If such a chain is stretched out by applying a force to the chain ends, the tensile force that tries to pull back the beads to its equilibrium position is

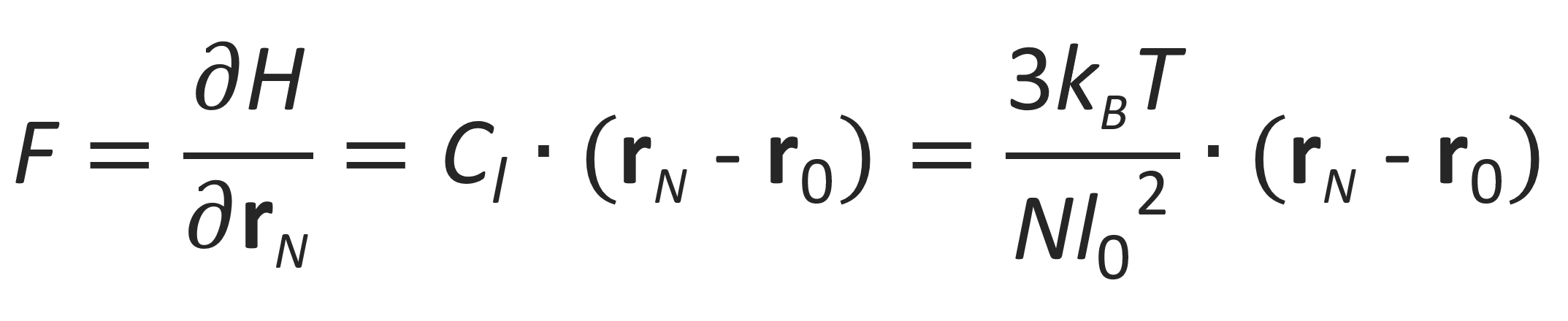
Note, the force constant is proportional to the absolute temperature. This has the important consequence that the elastic response of a polymer increases with increasing temperature. For this reason, a rubber band under constant stress contracts when it is heated instead of expanding as most materials do.

References & Notes

1. Gert Strobl, The Physics of Polymers, 3^rd Edition, Heidelberg 2007

2. Iwao Teraoka, Polymer Solutions, Wiley-Interscience, New York 2002

3. For a vinyl polymer, the contour length is identical with the end-to-end distance of the chain in an all-trans conformation.

4. The probability P(R) that a chain has its ends separated by a distance R = r_N - r₀ is given by

           

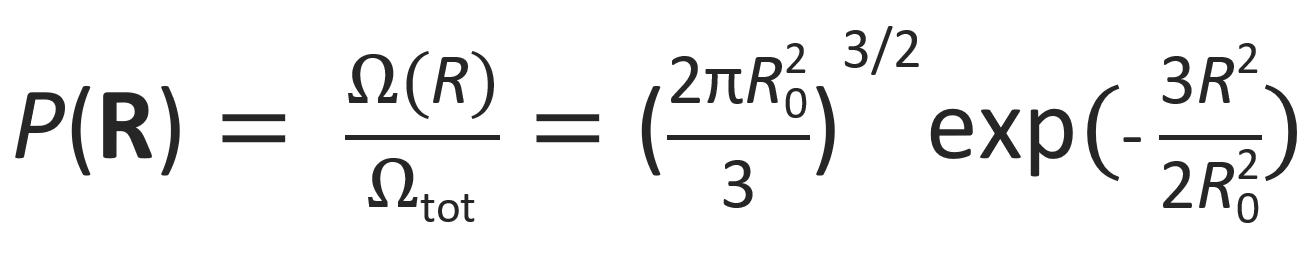
   where Ω(R) is the number of conformations of a chain having an (extended) end-to-end distance R and Ω_tot is the total number of conformations. Then the Helmholtz free energy is given by