Fracture in Plastics
and Griffith Criteria

Fracture of brittle plastics is often caused by defects such as cracks, scratches, inclusions, and pores that are created during processing, forming or service when the material is exposed to stress. Understanding the effect of these defects on the fatigue and break strength of a material is crucial for the prediction of the service life of a material under stress.  

The crack resistance (toughness) of a polymer depends on both intrinsic and extrinsic factors. Important intrinsic factors are molecular structure, cohesive energy, molecular weight (distribution), and morphology (degree of crystallinity) to name only a few factors. The propagation of cracks in a material also depends on extrinsic factors such as strain rate, temperature, stress state, specimen geometry, and notch or crack size and shape. Cyclic stressing is usually more severe than static stress, such that it will result in fracture well below the mechanical strength or yield point of the plastic. A high molecular weight and narrow molecular weight distribution generally improves fatigue and crack resistance whereas increased crystallinity lowers the fracture resistance. Elastic and viscoelastic deformation (yielding) is usually desired because it adsorbs some or all of the fracture energy, i.e. it stops crack growth. The same is true for inhomogeneous deformation such as crazing and shear banding. Polymers that yield are usually tougher than polymers that craze because the later absorbs less energy. For example, polystyrene tends to craze whereas polycarbonate tends to yield, because the two polymers have different chain structure. Thus, polycarbonate is much tougher than polystyrene.  

The theory of crack propagation was first investigated by Griffith in 1921.¹ He considered a homogeneous isotropic plate of negligible thickness, containing a crack in the shape of an ellipse. For this situation, lateral contraction of the plate can be neglected. He also assumed that the material is perfectly elastic.

Notch in a Thin Plate

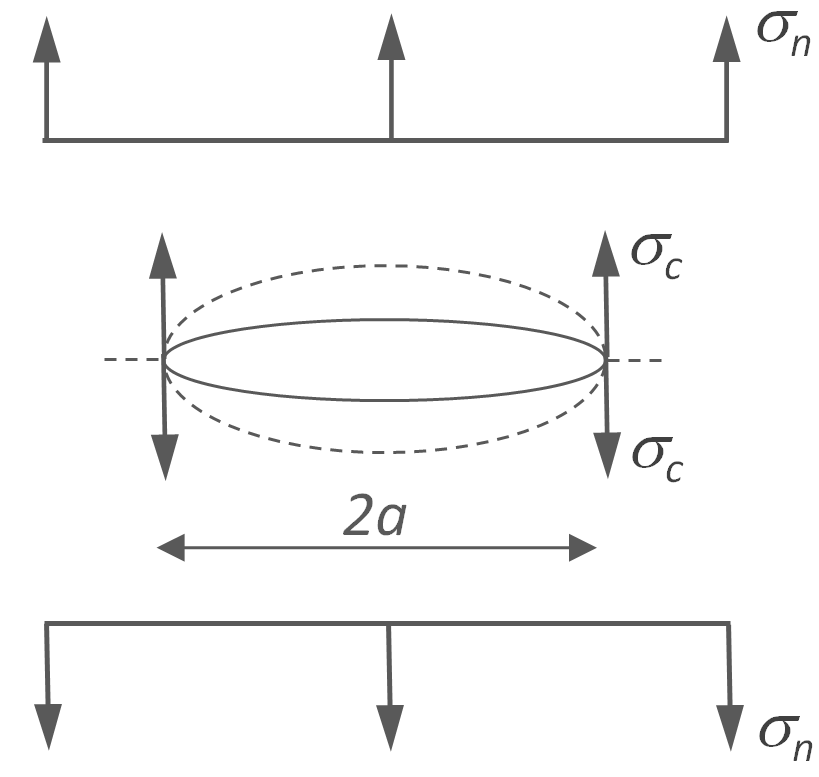
To further simplify the problem we assume a circular notch of radius a. The volume of the notch is π a²s and the strain energy per unit volume is ½ E ε² = ½ σ² / E. Thus, the strain energy released by the crack is simply ½ π a² s σ² / E. The potential energy of the crack is equal to the fracture surface energy Γ times its surface area, 2 π a s Γ, where s is the thickness of the plate. Griffith assumed that the crack is stable if the strain energy does not exceed the fracture surface energy, that is

∂/∂a [- ½ π a² s σ² / E + 2 π a s Γ] > 0

or

∂ΔW = (- π a s σ² / E + 2 π s Γ) ∂a > 0

The critical condition for crack propagation is ∂ΔW /∂a = 0, thus

σ_cr² = 2 Γ E / a 

where σ_cr is the critical breaking stress. This result is an approximation. Griffith calculation for elliptical cracks yields

σ_cr² = 2 Γ E / (π a)

The equations above are only valid for thin plates where lateral contraction can be neglected. For thick specimens the formula reads

σ_cr² = 2 Γ E / [π(1 - ν²) a]

where ν is the Poisson ratio. According to the Griffith equation, the breaking stress of a homogeneous plate, having a sufficiently long straight crack normal to the applied stress, is inversely proportional to the square root of the crack length. Thus, the larger the crack, the lower the brittle failure stress. The equation also shows that the stress for fracture is proportional to the strength of the internal physical and/or chemical bonds because the fracture energy Γ is a function of the cohesive energy of the material.

The Griffith equation is only valid for brittle materials such as glass and ceramic. Most plastics and metals undergo plastic deformation prior fracture unless the temperature is well below the material's brittle point. Plastic deformation is usually desired because it greatly increases the fracture strenght due to blunting of the crack tip. Thus, metals and plastics have much higher fracture energies than glassy materials. For plastic materials the Griffith model has to be modified to include energy dissipation through plastic deformation (see Irwin-Orowan extension of Griffith model).

References

1. A.A. Griffith, Philos. Trans. Roy. Soc. A, Vol. 221, Issue 582, p. 163 (1921)

2. M.D Lechner, K. Gehrke, E.H. Nordmeier, Makromolekulare Chemie, 1993