Fracture of Glassy Polymers
Cavitation and Crazing

Many fractures of brittle plastics are caused by cavitation and crazing. Cavitation is the formation of voids during deformation due to excessive stress. It is often a precursor to brittle fracture or crazing and a common phenomenon in semicrystalline brittle polymers. The voids or cavities can be in the range of a few nanometers to several micrometers. They usually form inside the amorphous phase between lamellae during deformation of the amorphous phase of the polymer. The formation of voids occurs only in tension whereas shear leads to the formation of shear bands. The voids usually form just before the material starts to yield or craze, i.e. cavitation precedes yielding and crazing.

A craze is defined as a microvoid which develops similar to a crack normal to the main stress/strain axis, usually via chain scission. However, in contrast to cracks, crazes can sustain stress due to the formation of fibrils of oriented chains that span from one face of the microvoid to the other (see figure below). These fibrils can make up 20 to 50% of the craze volume and can support noticeable tensile stresses. The fibrils are often only a few nanometers in diameter and therefore difficult to observe. However, these nanoscopic fibrills are quite strong. 

Crazing and Crack Propagation

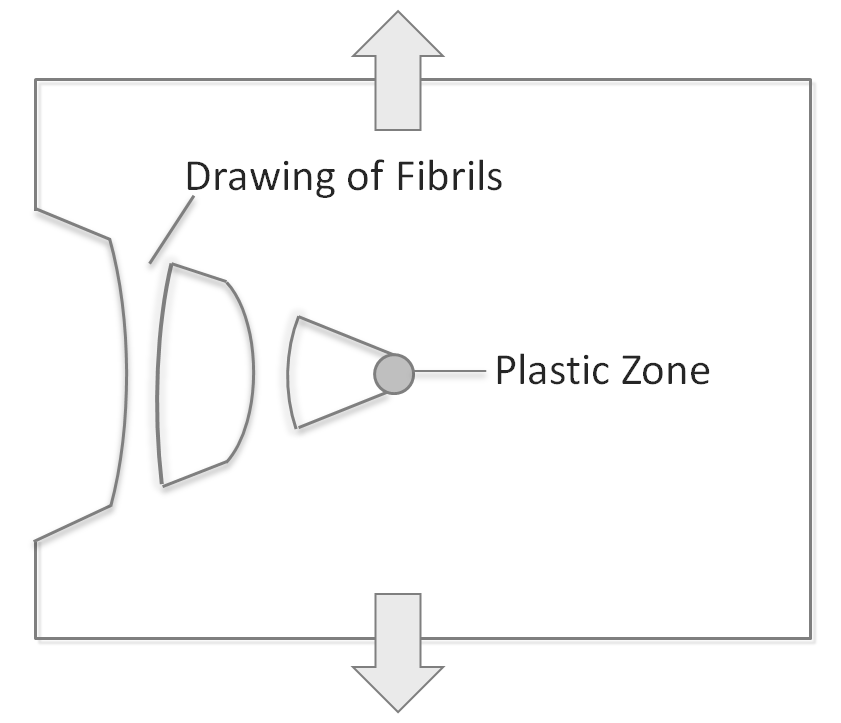
The fracture of the amorphous phase through cavitation and crazing competes with plastic deformation of the lamellar crystals. Which mechanism occurs first depends on the structure of the two phases. If the crystals are weak and full of imperfections, their deformation occurs without cavitation and mostly via chain slippping. If, however, the crystals in a polymer are thick and more perfect then the energy barrier for their deformation is rather high and cavitation starts first followed by crazing.

Which failure mode dominates depends on many factors. Important intrinsic factors of the crystal phase are crystal structure, crystal thickness, and degree of crystallinity, and those of the amorphous phase are free volume, and entanglement density. Important extrinsic factors are temperature and rate of deformation, stress state, specimen geometry and the number, size and shape of defects such as notches or cracks.  

 

Critical Stress for Cavitation

Materials will only undergo cavitation (around defects) if the energy for cavitation is at least equal to the strain energy. Assuming a cavitation around a defect of size r, the energy for the formation of the void is equal to the fracture surface energy Γ times the surface area of the defect, E_cav = 4 π r² Γ. The released strain energy per unit volume is ½ E ε² = ½ σ² / E. Thus, the strain energy released by the void is simply E_str = 2/3 π r³ σ² / E. Assuming E_str  - E_cav = 0, gives

σ_cav² = 6 Γ E / r 

Depending on the material properties, the defect size, and temperature, the material can either undergo local yielding, i.e. crazing or the defect (void) can initiate brittle fracture. The critical stress for crack growth can be calculated with the Griffith criterion. Griffith postulated that a crack only propagates if the energy
release rate during crack growth (or void formation) does exceed the rate of increase in fracture surface energy.¹

σ_cr² = 2 Γ E / (π r)

where σcr is the critical breaking stress for a defect of size r. Comparing this result with the critical stress for void formation gives

σ_cr² ≈ 2 Γ E / (3 r) ⇒ σ_cr = σ_cav / 3

This means in an ideal elastic (brittle) material, crack growth is always the dominating failure mode.² However, polymers are not ideal elastic but tough materials that tend to yield before fracturing. They either craze - i.e. they form microvoids which cause local yielding - or they yield on a macroscopic scale, whereas brittle (catastrophic) failure without noticeable deformation (yielding) is only observed at very low temperatures well below the brittle point.

References and Notes

1. A.A. Griffith, Philos. Trans. Roy. Soc. A, Vol. 221, Issue 582, p. 163 (1921)

2. I (semi-crystalline) polymers, the fracture surface energy around a defect, Γ_loc, can be much smaller than the surface fracture energy in the homogeneous phase Γ. Thus, energy can be dissipated through plastic deformation around voids without causing catastropic crack propagation. In fact, void formation and localized yielding around small defects is a common phenomenon in semi-crystalline polymers and can greatly improve the fracture toughness of a polymer.