Scaling Laws

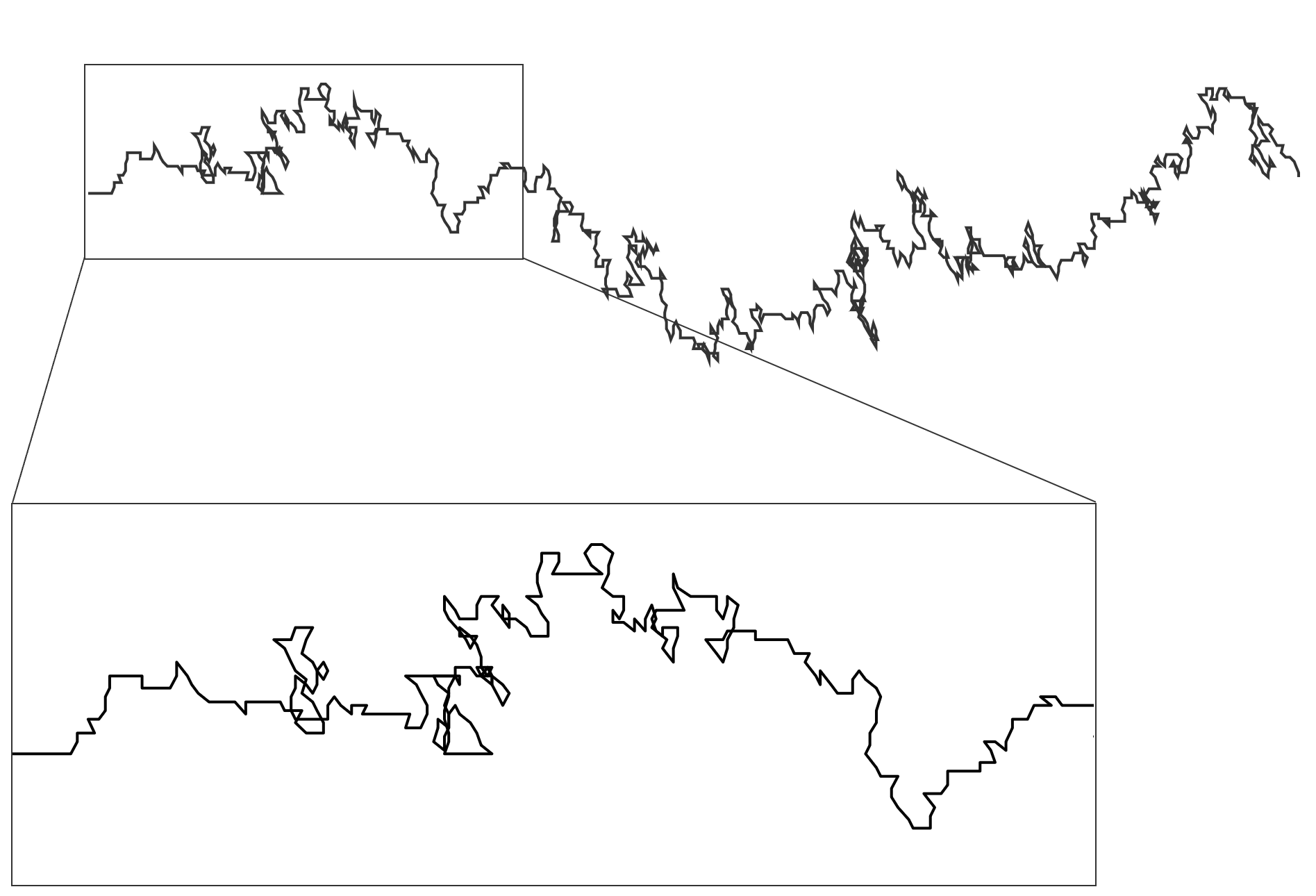
Two of the most powerful concepts in polymer physics are universality and scale invariance. It was found that polymers with very different microscopic structure all have a very similar macroscopic behavior and obey the same universal power laws regardless of their chemical structure if they have the same macroscopic structure (polymer topology); the only difference is the pre-factor in front of the functions. Furthermore, polymers are self-similar like fractals, meaning they look the same at different length scales (resolutions) and thus exhibit the same internal structure and must obey the same scaling laws (scale invariance). In other words, the physical laws should be independent of the scale at which they are observed.

Segmented Chain

Then any spatial property such as the mean-square end-to-end distance or the radius of gyration must scale with the number of steps, N. The functions that relate these properties to the degree of polymerization, N, are known as scaling or power laws:

⟨R_x²⟩^1/2 ∼ N^ν

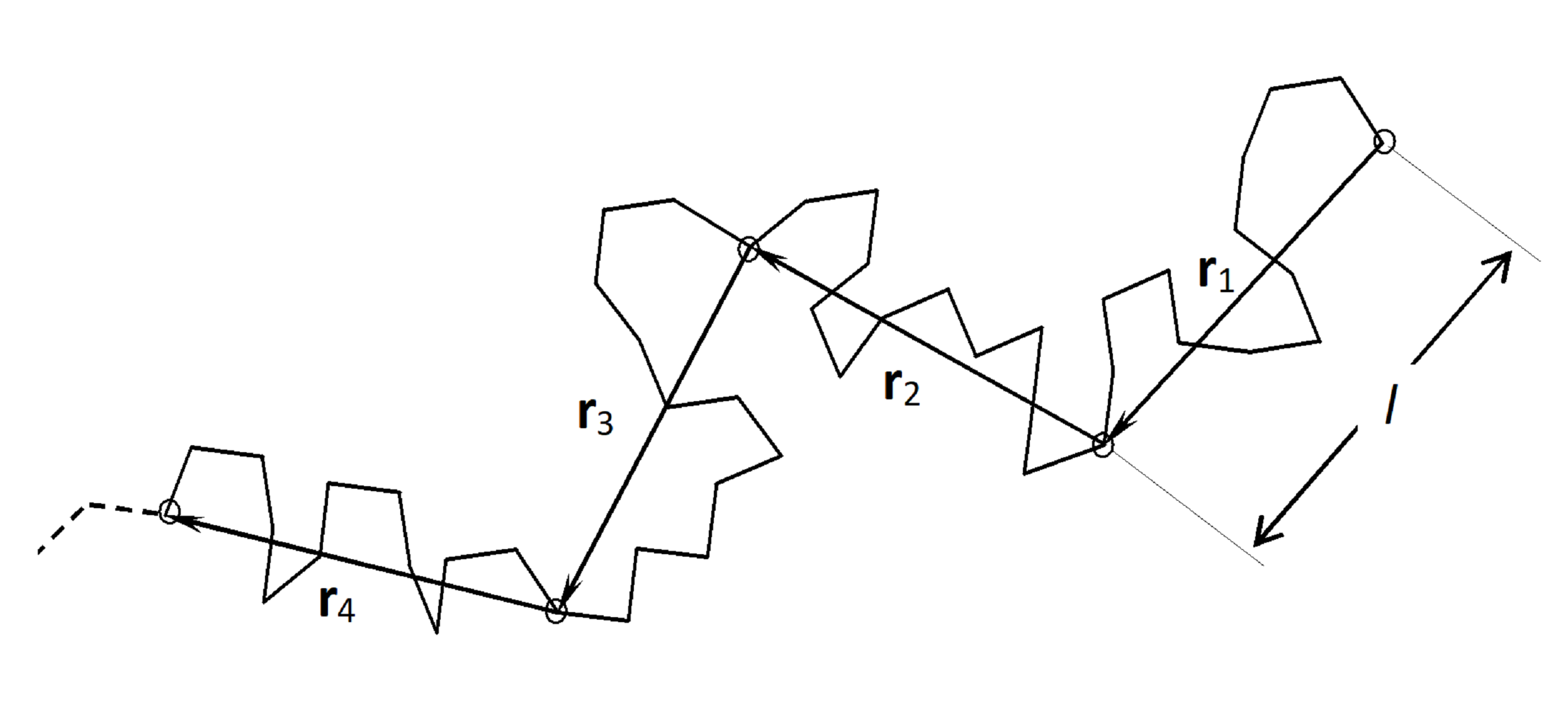
To simplify calculations, a polymer chain is often replaced by a model chain consisting of N statistical segments of length l. Each segment represents a small number of repeat units in the real chain. However, the scale we chose for the length of the links, l, and the number of corresponding statistical segments, N = L/l, is arbitrary as long as the contour length L = Nl of the model chain is equal to that of the real chain.¹

To explain the method of scaling, let us consider a Gaussian chain (also called freely jointed chain) that consists of N statistical segments. Let us group λ segments to a new segment. Then the number of new segments is simply N/λ and the length of each new segment is λ^1/2l:

N → N/λ,  l → λ^1/2l

If a function is scale-invariant, the macroscope properties should be the same at all length scales.¹ For example, the average end-to-end distance ⟨R²⟩ should not change under the above transformation. Then any physical property should obey following scaling law:

f(N/λ, λ^1/2l) = f(N, l)

As has been shown with renormalzation theory, chains with long-range interaction satisfy a similar scaling law:

f(N/λ, λ^νl) = f(N, l)

where ν is the so-called scaling exponent which has the value 1/2 for ideal chains and approximately 3/2 for exluded volume chains. Furthermore, it was shown that any property of a flexible chain such as the end-to-end probability distribution, G(R, L), is scale-invariant if^2,6

A(l λ^ν, N/λ) = λ^x A(l, N)

For the end-to-end probability distribution, G(R, L), this expression can be written as⁶

G(Rλ^ν, Lλ) = λ^x G(R, L)

In the case of spatial quantities such as the mean end-to-end distance, R ≈ N^νl, the exponent x is zero:

R(N λ^-1, l λ^ν) = l λ^ν (N / λ)^ν = λ⁰ N^νl = N^νl

Another important scale-invariant quantity is the mean segment concentration in a polymer coil: The coil size is of the order N^νl, and thus its volume is approximately N^3ν l³.⁸ This volume contains N polymer units. Then the mean concentration is equal to

c ≅ N / (l³ N^3ν) = l^-3 N^{1- 3ν}

For this simple scaling law, x is equal to -1:

c₂(N λ^-1, l λ^ν) ≅ (l λ^ν)^-3 (N / λ)^{1- 3ν} = λ^-1 l^-3 N^{1- 3ν} = λ^-1c

This result is obvious, because if the number of segments has been reduced to N / λ, the segment concentration will be reduced by the same factor λ^-1, because the coil volume is independent of the segment length.

The fact that polymers possess scale-invariance, i.e. that they are self-similar on a range of (finite) length scales, means they are random fractal objects. The fractal dimension D of such objects can be expressed by the exponent in the power law that relates the number of segments, g, in any section of the polymer to the root-mean square distance, ⟨R²⟩^1/2:^5,7

g ∼ (⟨R²⟩^1/2)^D

Hence, the fractal dimension of a freely-jointed or Gaussian chain is D = 2, because N ∝ R², whereas a polymer chain with excluded volume interaction has the fractal dimension D ≈ 5/3 = 1.7.

The scaling theory has been successfully applied to solve numerous problems in polymer physics. The results of these investigations have been summarized in several polymer physics books. Three excellent books that give comprehensive insight into this topic are Pierr-Gilles De Gennes' book Scaling concepts in Poylmer Physics, Polymer Physics by M. Rubinstein and R.H Colby and Statistical Physics of Macromolecules by A.Y. Grosberg and A.R. Khokhlov.

References, Notes & Further Readings

1. Note, self-similarity holds only for a finite range; the upper bound is obviously equal to the size of the polymer coil, R₀, whereas the lower bound is equal to the minimum number of repeat units that have to be combined to a statistical segment to achieve random walk behavior. This length is equal to twice the persistence length 2l_p and is the smallest scale.

2. M. Doi, Introduction to Polymer Physics, Oxford Science Publications (1995)
3. M. Doi, S.F. Edwards, The Theory of Polymer Dynamics, Oxford University Press, New York 1986
4. P.G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, Ithaca, NY, 1970
5. Gert Strobl, The Physics of Polymers, 3rd Edition, Heidelberg 2007
6. S.M. Bhattacharjee, A. Giacometti, A. Maritan, Flory theory for Polymers, J. Phys.: Condens. Matter 25, 503101 (2013)
7. A. Y. Grosberg, A.R. Khokhlov, Statistical Physics of Macromolecules, AIP Press, Woodbury, NY 1994
8. Note, all constant prefactors have been omitted.