More Topics:

Cohesive Energy and Lennard-Jones Potential

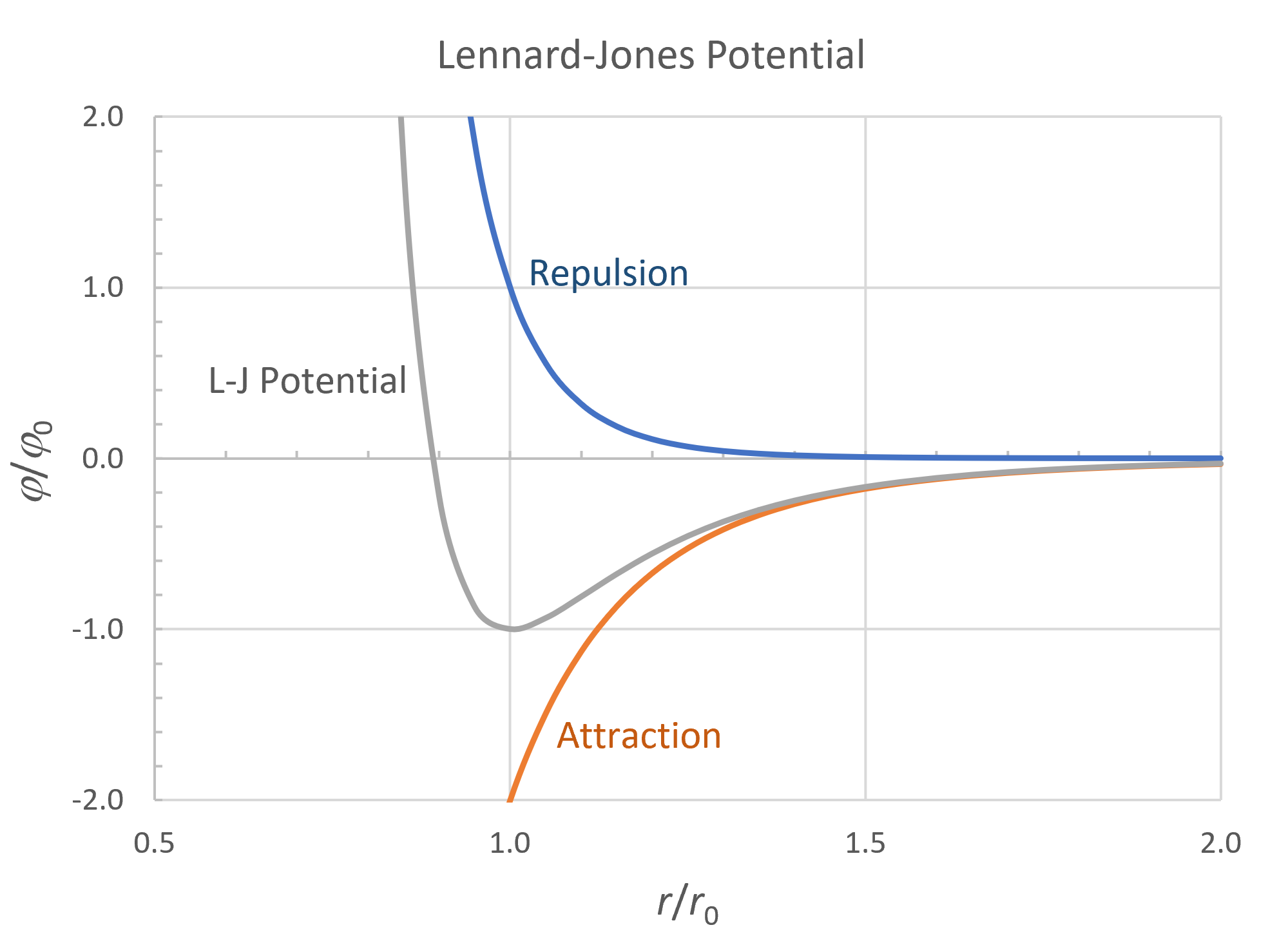
The cohesive energy is one of the most important properties of polymers. It can be derived from the depth of the molecular potential well. If no specific interactions are present, the well depth is the minimum of the Lennard-Jones potential:1

φ = φ0 · [(r0 / r)12 - 2(r0 / r)6 ]

φ0 is the energy responsible for the strength of a material. To be more specific, it is the energy that has to be overcome by mechanical and thermal energies to deform the material, and therefore, determines the magnitude of the bulk thermo-mechanical properties of a polymer.

The equivalent bulk parameter to φ is the cohesive energy, Ecoh. It is defined as the energy per mole required to eliminate all intermolecular forces.2 As has been shown by Porter,3 the potential function can be expressed as a function of the cohesive energy.

CROW logo

To expresse the interaction potential as a function of the cohesive energy, we first need to convert the volume of a repeat unit into the molar van der Waals volume. This volume is connected to the intermolecular distance r by

V = Navo r3 / q

where Navo is the Avogadro's number and q is a constant that corrects for the geometry of the repeat units. On substituting the molecular distances with the volumes, one arrives at the following relationship between volume and intermolecular distance:

V0 / V = (r0 / r)3

where V0 is the molar volume at the minimum in the potential well which is set equal to the molar volume of the (glassy) polymer at 0 K. If we assume a hexagonal interaction cells, then there are six interactions per unit cell with two mer units per interaction, i.e. 3 φ0 is the total interaction energy per unit cell. The corresponding volume of this interaction is approximately four mer unit volumes, so that the energy density equals

e0 = 3 Navoφ0 / (4 V)

or

φ0 = 4 Ecoh / 3Navo ≈ Ecoh / 4.5 · 1023

where Ecoh is the cohesive energy in units of J/mol and φ0 is in units of J/(mer-unit interaction). Substituting the expressions for φ0 and r0 / r into the Lennard-Jones equation, the total potential energy per mole of a material reads4

W ≈ K Ecoh · [(V0 / V)4 - 2(V0 / V)2 ]

where K is a numerical fitting parameter which has a value of about two at room temperature.4 The cohesive energy has a considerable advantage over φ0 as an input parameter in models. For example, it can be calculated with group contribution methods and for many compounds experimental values have been reported, whereas the literature on φ0 is rather sparse.

References, Notes & Further Readings
  1. J. E. Lennard-Jones and W.R. Cook, Proc. R. Soc. A, 112 (760), 214-229 (1926)

  2. In the case of low molecular weight compounds, the cohesive energy is equal to the energy required to evaporate the material:

    Ecoh ≈ ΔHvap - RT

  3. FD. Porter, Group Interaction Modelling of Polymer Properties, Marcel Dekker, New York (1995).
  4. J.T. Seitz, J. of Appl. Poly. Sci., Vol. 49, 1331-1351 (1993)
  5. A.A. Askadskii, Computational Material Science of Polymers, Cambridge Int. Sci. Publ. 2003

  • Summary

    Lennard-Jones Potential

    describes the nonbonded intermolecular interaction between polymer repeat units. It is the energy that has to be overcome by mechanical and thermal energies to deform a material.

  • Cohesive Energy

    is defined as the energy per mole of material required to eliminate all intermolecular forces. In the case of low molecular weight compounds, it is the energy required to evaporate the material.

  • The cohesive energy determines the magnitude of the bulk thermo-mechanical properties of a polymeric material.

  • The cohesive energy and the related parameters are of great importance in polymer physics, because many thermophysical and mechanical properties are directly related to the cohesive energy.

  • For example, linear relationships were found between the cohesive energy, the heat capacity, and the shear modulus.