Group Interaction Modeling
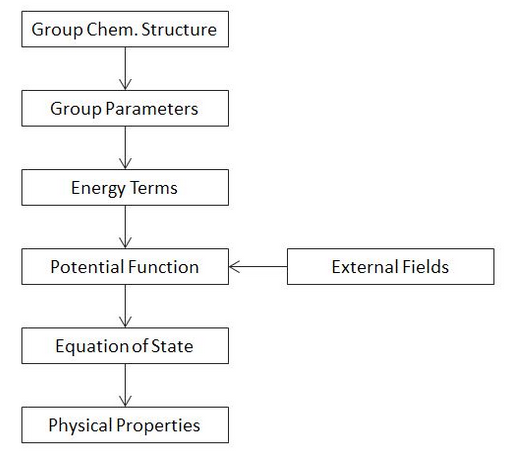
As the name suggests, group interaction modeling (GIM) uses the intermolecular energy of interaction between groups of atoms in adjacent polymer chains as a basis for the prediction of important thermo-physical properties of condesed matter. All properties are predicted as a function of chemical composition and micro- and macromolecular structure. GIM combines the concept of cell models with the PRISM theory. The model is based purely upon energy balance of repulsive and attractive intermolecular forces and thermodynamic energies. Furthermore, GIM makes use of a mean field approach, which allows for the development of simple enough models that include all important structural effects. The steps involved in the GIM approach to predict physical properties are shown in the flow chart below.
The structural unit of the polymer is the smallest chemical grouping in the polymer chain that contains all the structural components to be modeled. For a homopolymer, we can choose a mer unit. The size of the group is assumed to be irrelevant, since all parameter scale identically with the size of the group. Each mer unit is surrounded on all sides by by other single (identical) mer units. A hexagonal arrangement of lattice cells is assumed, that is, each central mer unit is surrounded by six adjacent, non-chemically bonded and two chemically bonded mer units. This means the mean interaction cell contains in total 9 mer units with 6 pairwise interchain mer unit interaction. To each characteristic structural unit of the polymer a set of input parameters for the modelling is assigned. Two different types of input parameters exist. The first are simple dimensional parameters, such as the van der Waals volume, the molar mass, and the (average) length of a unit along the chain axis. The second set of parameters are needed for the calculation of the different kinds of energies of the polymer, these are the cohesive energy, and two additional parameters that are needed for the calculation of thermal energies, which are the reference temperature for the heat capacity and the number of skeletal vibrational modes (or degree of freedom). With the exception of the last two, all parameters are assigned simply by means of group contribution methods.
The GIM method works well for most volumetric and energetic parameters. It uses both energy and dimensional parameters to predict properties from potential functions. For example, the cohesive energy is proportional to the depth of the potential well of the interaction energy of the Lennard-Jones function and the van der Waals volume to the volume at zero point energy position. The thermal energy of skeletal vibrations in the polymer chain is calculated with the Tarsov extension of the Debye theory of specific heat capacity, which allows for modelling important parameters of GIM. The potential function is at the heart of the GIM theory. The properties are calculated from the energy balance of all involved intermolecular energies. In many cases, the equation of state can be readily solved to predict the property in question.
References
- D. Porter, Group Interaction Modelling of Polymer Properties, Marcel Dekker, New York (1995)