Topology in Polymer Physics
Topological methods have been proven to be very useful in predicting many properties of polymers. These methods are based on graph-theoretical concepts and were first introduced by Harry Wiener during the years 1947-1948. Wiener investigated the physical and chemical properties of a series of (branched) alkanes such as boiling point at atmospheric pressure, heat of isomerization, and heat of vaporization.1-3 He postulated that these properties depend solely on the number, kind and structural arrangement of the atoms. In the case of alkane isomers, the kind and number of atoms is constant. Then the variations in the property in question depend solely on the structural arrangement of the atoms. He further assumed that these properties would satisfy a linear formula of the type
X = a · W + b · P + c
where a, b and c are two constants for a given isomeric group and W and P are two topological indices defined by Wiener1 and described below.
To calculate property values, Wiener wrote his equations as differences by subtracting from the equation above an equation of same type for normal alkanes:
ΔX = a · ΔW + b · ΔP + c
For example, for the boiling point of paraffins of any lenght, Wiener obtained from a least squares fitting procedure1
ΔTb = (98/n2) · ΔW + 5.5 · ΔP + c
The average deviation in the boiling point was found to be less than 0.5°C.1
Topological Graph Indices
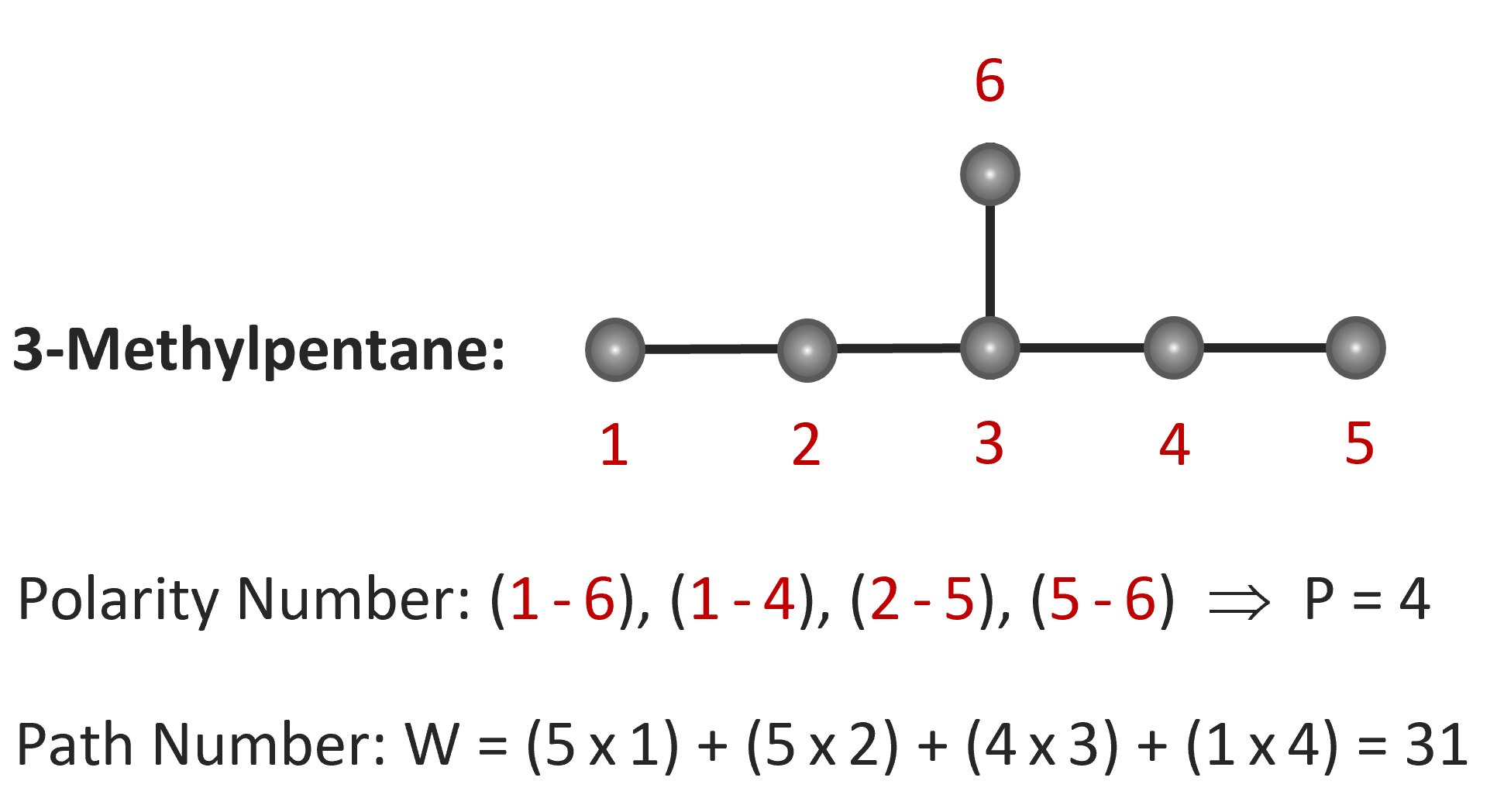
The topological index P is defined as the total number of pairs of carbon atoms which are separated by three carbon-carbon bonds (two carbon atoms) and the index W is defined as the sum of distances between any two carbon atoms in terms of carbon bonds. Wiener termed these two topological indices the polarity number (P) and the path number (W). The latter is often called the Wiener number. The calculation of these indices is illustrated below for 3-methylpentane.
The Wiener index has been also applied to macromolecules. For example, the mean-square radius of gyration Rg2 can be directly calculated from the Wiener number:4,5
Rg2 = l2 · W / N2
where l is the length of a statistical segment and N is its number. This finding is not surprising since 2W / N2 is the average distance in the distance matrix, also called the topological radius.5 A related structural property, the Zimm-Stockmayer branching ratio, is equal to the normalized Wiener number of the respective (hydrogen-supressed) polymer graph:4,5
Rg2 / Rg,lin2 = W / Wlin = W'
where Rg,lin2 is the mean-square
radius of gyration of a linear chain having the same number of
statistical bonds.
Many other properties can be calulated with
the Wiener number. For example, the zero-shear viscosity of polymer melts and solutions
can be obtained from6
η0 = c ζ Rg2 / 6 = c ζ l2 W / 6N2
wheer ζ is the friction coefficient and c is the number of polymer chains per unit volume.
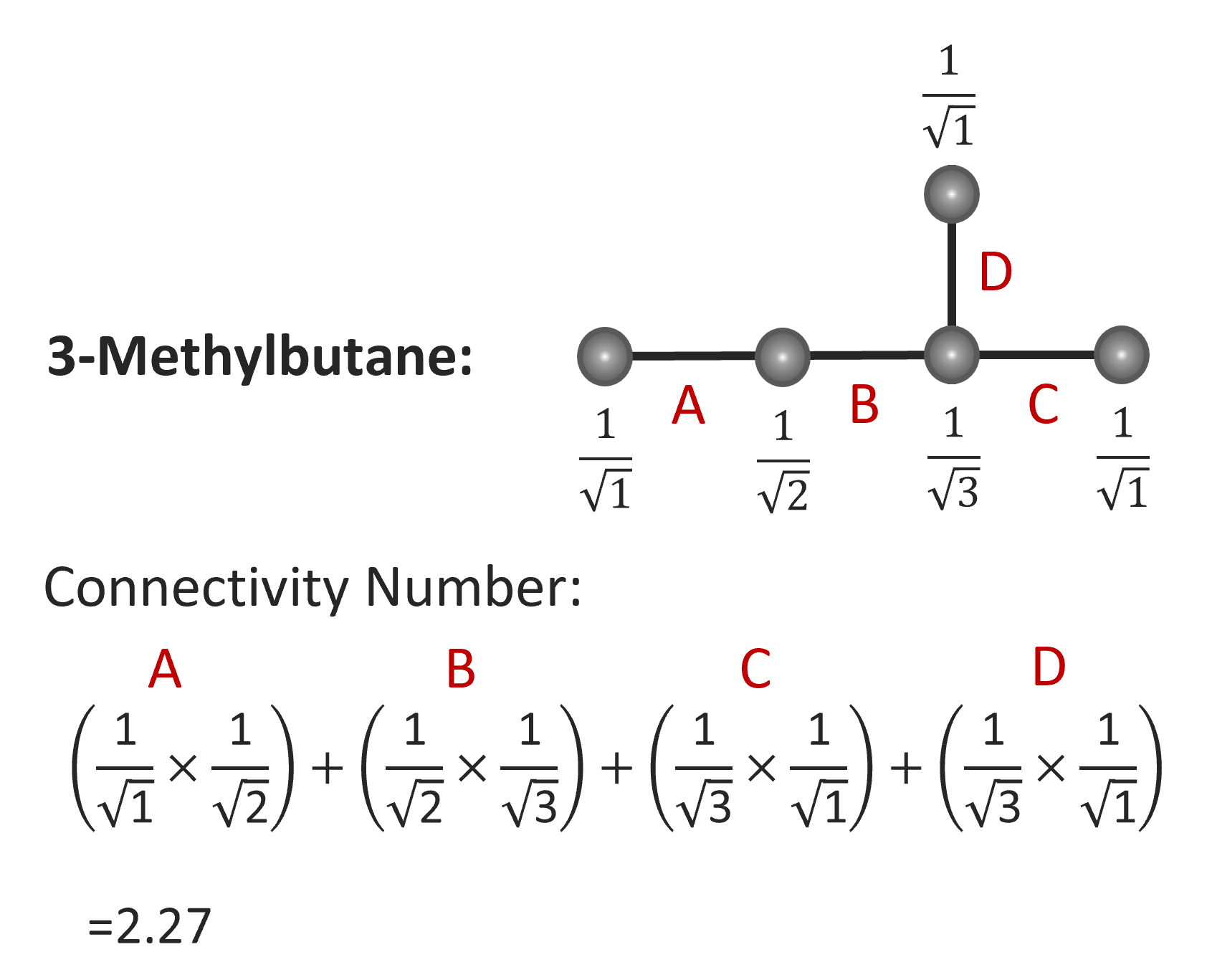
Over the last three decades, a large number of other topological indices have been introduced. For example, Randic introduced the molecular connectivity index χ to describe the effect of the degree of branching on properties. It is defined as the inverse sum of bond weights:7
1χ = ∑i,j (δi δj)-1/2
Here δi and δj are are the degrees of adjacent vertices i and j, respectively. The calculation of this index is illustrated below for 3-methylbutane.8
Many other connectivity indices have been proposed. The simplest is the zero-order connectivity index defined as10,11
0χ = ∑i δi-1/2
Kier, Hall and others generalized the connectivity index by considering paths along the molecular graph of length h:10
1χ = ∑i,j (δi δj, ..., δh)-1/2
where the sum is taken over all possible paths of length h. These indices are also known as h-order connectivity indices.
The indices above do not distinguish between different types of backbone atoms. However, many properties depend on the type of atoms in the molecular graph. For this reason, Kier and Hall defined the valence connectivity index which is calculated from the number of valence electrons, Ziv, and the number of hydrogen atoms bonded to the atoms, NH,i:4,13
δiv = Ziv - NH,i
The valence connectivity indices are calculated by replacing δi with δiv in the equations above. For example, the first-order valence connectivity index is given by11,12
1χv = ∑i,j (δiv δjv)-1/2
The table below shows the δ and δv values of carbon atoms for different states of hybridization.
| Hybrid | NH | δ | δv |
| sp3 | 3 | 1 | 1 |
| 2 | 2 | 2 | |
| 1 | 3 | 3 | |
| 0 | 4 | 4 | |
| sp2 | 2 | 1 | 2 |
| 1 | 2 | 3 | |
| 0 | 3 | 4 | |
| sp | 1 | 1 | 3 |
| 0 | 2 | 4 |
Topological Indices of Polymer Graphs
Bicerano and others14 have shown than many thermodynamic properties of polymers such as the Van der Waals volume, cohesive energy, heat capacity, and glass transition temperature can be predicted with (linear) equations in χ and χv:
ΔX = a · 0χ - b · 1χv
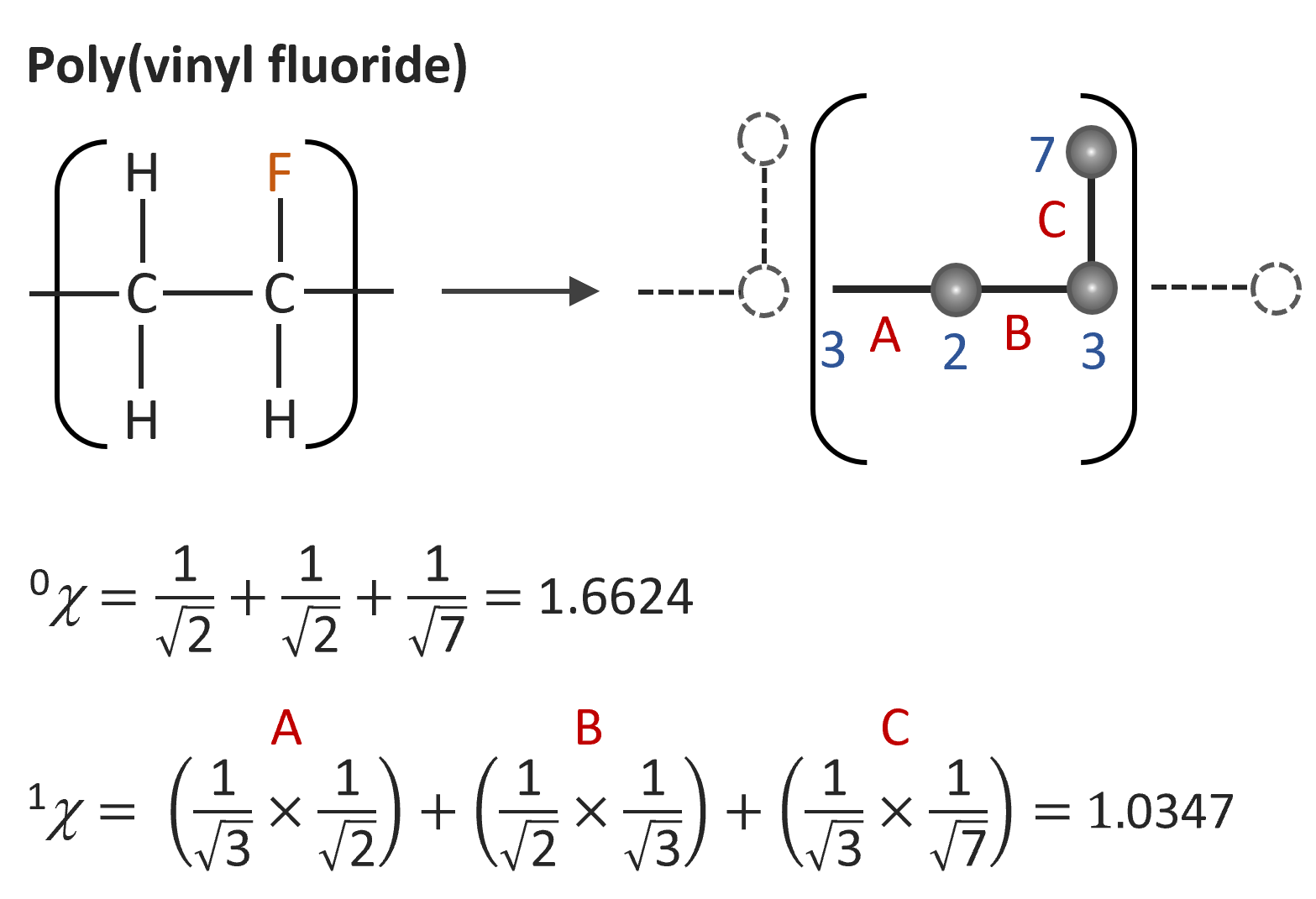
To simplify the problem, Bicerano replaced the molecular graph of the entire polymer with that of a repeat unit with one connecting edge inside and one outside the repeat unit.14 An example is shown below.
Using this simplified molecular graph and a linear regression analysis, many properties of polymers can be predicted with reasonable accuracy. For example, for the van der Waals volume, Biccerano obtained from a least-squares fitting procedure14
VVdW ≈ 3.861 0χ - 13.7481χv
This two-parameter regression has a standard deviation of about 4.5 cc/mole and a correlation coefficient of 0.996.14,15
Distance and Adjacency Matrix
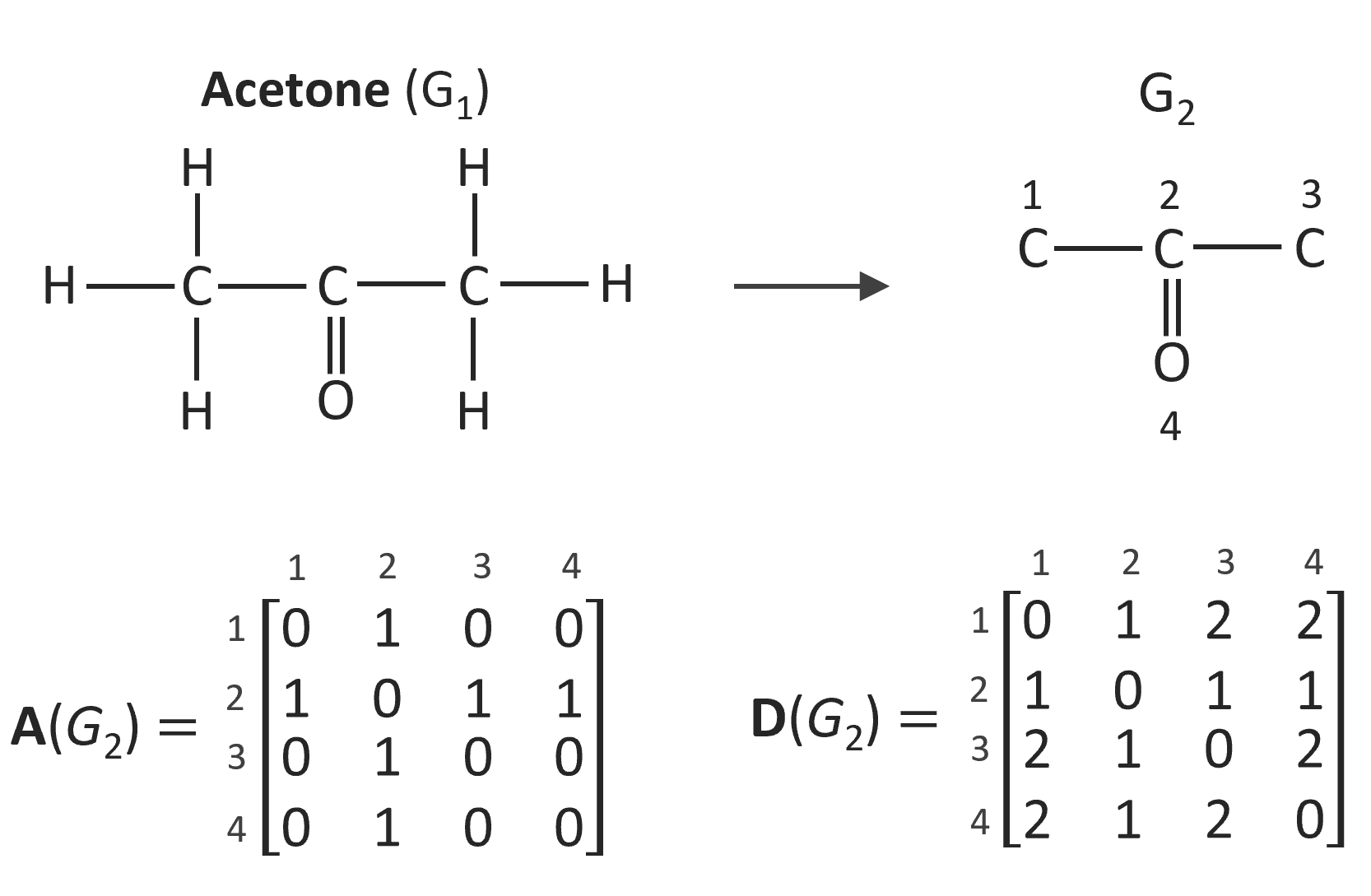
Many topological indices can be conveniently calculated from various matrices. For example, the Wiener number can be calculated from the so called distance mantrix:
W = ½ ∑i,j di,j = ½ (u · D · uT)
where D(G) is the distance matrix of a hydrogen-suppressed molecular graph G with n vertices. This matrix is a symmetric n x n matrix (di,j) where di,j is the distance between vertex vi and vj. Another important representation of a graph G is the adjacency matrix A(G). This matrix is a n x n symmetric matrix as well. The ai,j entries of this matrix have only the values 0 and 1; ai,j is equal to one if the vertices vi and vj are adjacent and zero otherwise. The two matrices for the labeled hydrogen-supressed molecular graph of acetone G2 are shown below.
A topological index that can be directly calculated from the adjacency matrix is the Randic index:4
1χ = ∑i,j (δi δj)-1/2 = ½ (v · A · v'T)
where v is a vector of vertex degrees and v' of vertex degrees raised to the power -½: v' = (δ1-½, δ2-½, ..., δn-½).
References and Notes
- H. Wiener, J. Am. Chem. Soc., 69, 1, 17-20 (1947)
- H. Wiener, J. Am. Chem. Soc., 69, 11, 2636-2638 (1947)
- H. Wiener, J. Phys. Chem., 52, 6, 1082-1089 (1948)
- D.H. Rouvray, R.B. King, Topology in Chemistry, Horwood Publishing 2002
- J.L. Gross, J. Yellen, P. Zhang, Handbook of Graph Theory, CRC Press, New York 2014
- Y. Yang, Macromol. Theory Simul. 7, 521-549 (1998)
- M. Randic, J. Am. Chem. Soc., 97, 23, 6609 - 6615 (1975)
- D.H. Rouvray, Sci. Am., Prediction Chemistry from Topology (1986)
- N. Trinajstic, Chemical Graph Theory, 2nd Ed., CRC Press 1992
- L.B. Kier, L.H. Hall, Molecular Connectivity in Chemistry and Drug Research, AP 1976
- L.B. Kier, L.H. Hall, Molecular Connectivity in Structure-Activity Analysis, 1st Ed., Wiley 1986
- L.B. Kier, L.H. Hall, J. Pharm. Sci., 65, 1806 (1976)
Kier and Hall calculated the valence delta δv with
δiv = (Zv,i - NH,i) / (Z - Zv,i - 1).12
where Zi is the total number of electrons of the atom represented by the ith vertex. For the most common elements C, N, O, both versions of the valence connectivity number yield identical values, because these elements have only two elelctrons in the inner shell, thus Z - Zv,i -1 = 1.11- Jozef Bicerano, Prediction of Polymer Properties, Marcel Dekker, New York 2002
- The method is only applicable to very long polymers because it neglects the effect of the end groups on the properties.
December 29, 2019; Revised February 8, 2020