Van der Waals Volume
The van der Waals volume of a molecule can be defined as the space occupied by the molecule, which is impenetrable to other molecules at ordinary temperatures. For an approximate calculation, the Van der Waals volume is assumed to be bounded by the outer surface of the interpenetrating spheres. The radius of each sphere is assumed to be the constant atomic radius of the element involved and the distance between the centres of two spheres of chemically bonded atoms is the (constant) bond length d. The contribution of a given atom with radius R to the van der Waals volume is then given by following simple geometric relation:
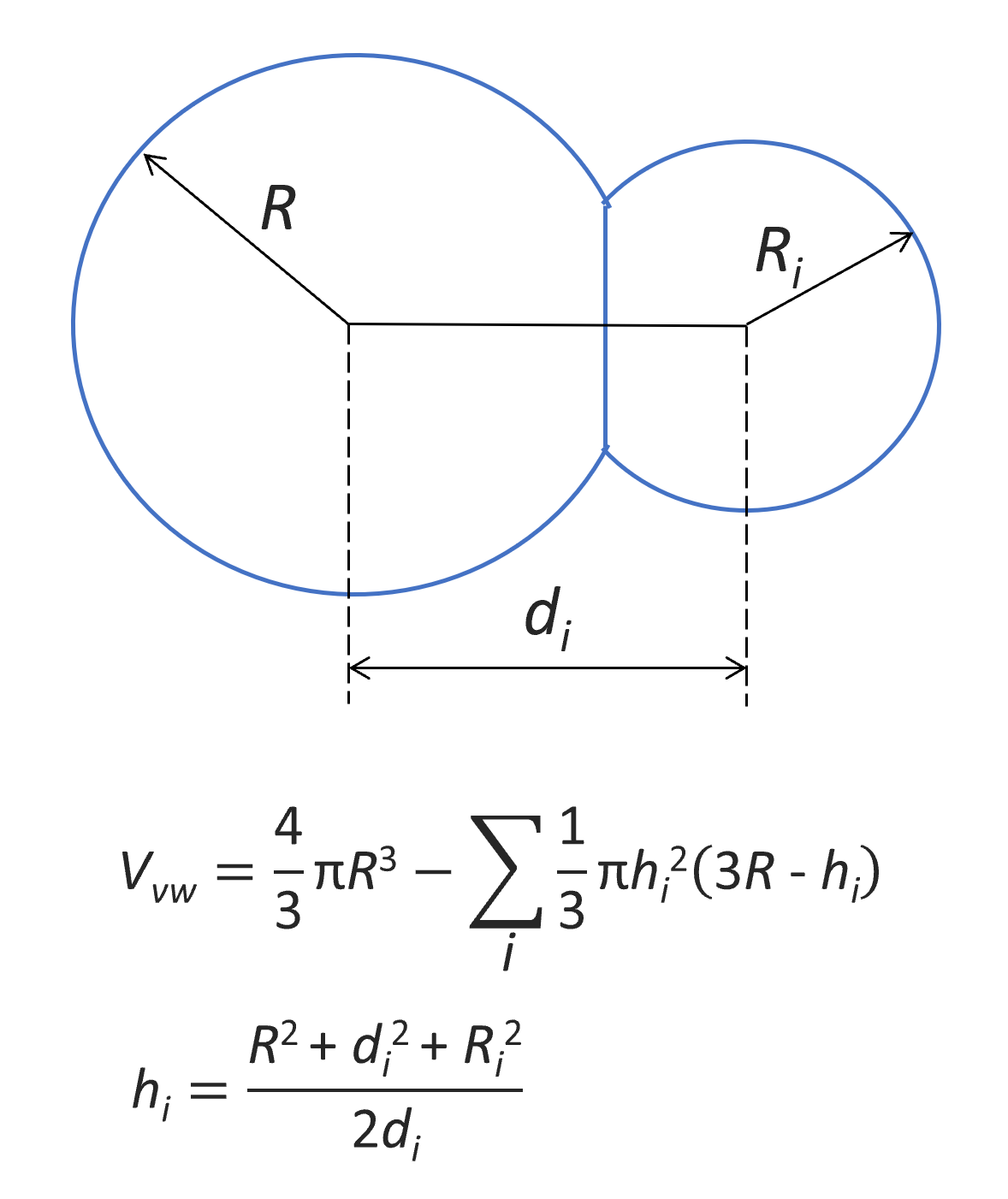
The van der Waals volume of a polymer repeat unit can approximately be calculated as the sum of the van der Waals volumes of the composing structural groups (group increments):
Vvwk = ∑k Nk · Vvdw,k
The true volume will be slightly different since the group contribution of each atom (Vvdw,k) in an increment is not constant but depends on the nature of the surrounding atoms. However, the volume contribution of each structural group already contains most of the inbuilt information on the influences of the atomic surroundings with the exception of the terminal bonds, and therefore, the approximation is valid as is shown in the examples below.
| Compound | Lit. Vvdwa cm3/mol | GC Vvdwb (cm3/mol) |
| Polymethylmethacrylate | 58.5 | 57.2 |
| Polycarbonate (PC) | 144.3 | 140.9 |
| Polyisobutene | 41.6 | 41.1 |
| Poly(caprolactame) (Nylon 6) | 64.4(c) | 68.8 |
| Polystyrene (PS) | 66.9 | 66.3 |
| Polyacylonitrile | 32.6 | 32.5 |
| Polyethylmethacrylate | 69.1 | 66.5 |
| Poly(ethylene terephthalate) | 94.2(c) | 96.3 |
References
- Andrey A. Askadskii, Computational Materials Science of Polymers, 1st ed., 2003
- D.W. van Krevelen and Klaas te Nijenhuis, Properties of Polymers, 4th Edition, Amsterdam 2009