Entropy Continuity
and Discontinuity in Specific Heat at Tg

At the glass transition, we can assume a two-phase equilibrium, that is, the pure-component specific entropies in the liquid (rubbery) and glassy state should be identical:

S_glass(T,p) = S_liq(T,p)

and at constant pressure or temperature:

(∂H / ∂T)_p = T(∂S / ∂T)_p = C_p

(∂S / ∂P)_T = -(∂V_m / ∂T)_P = -V_m · α

where α is the coefficient of volumetric thermal expansion and V_m the molar volume. Inserting these two equations into the thermodynamic continuity statement

(∂S_glass / ∂T)_pdT + (∂S_glass / ∂P)_Tdp = (∂S_liq / ∂T)_pdT + (∂S_liq / ∂P)_Tdp

gives

C_{p, glass} d lnT - V_m,glass α_glass dp = C_p,liq d lnT - V_m,liq α_liq dp

or

(∂ lnT_g / ∂P) = ( V_m,liq α_liq - V_m,glass α_glass) / ( C_p,liq - C_p,glass)

Discontinuity at Glass Transition

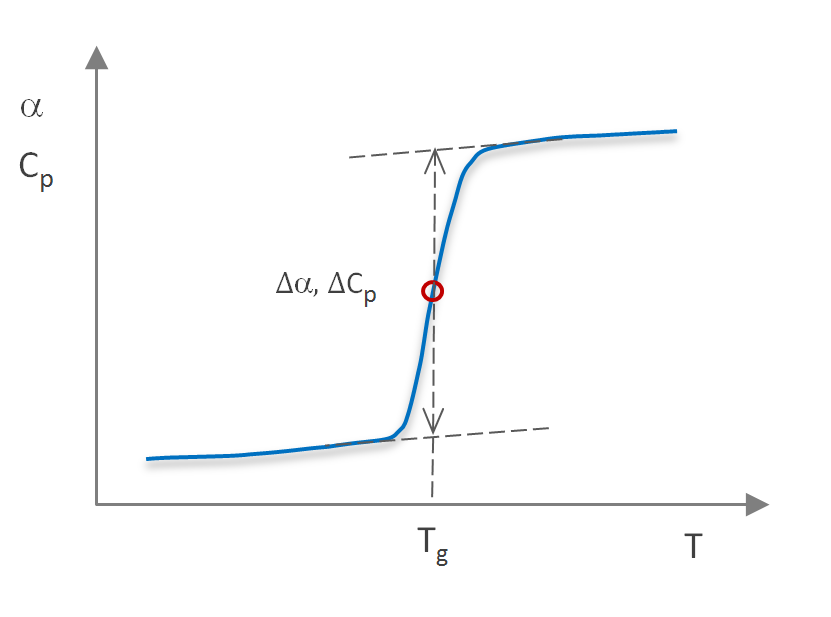
Since volume continuity at T_g requires that V_m,glass = V_m,liq, this expression reduces to

(∂ lnT_g / ∂P) = V_m Δα / ΔC_p
or
(∂ T_g / ∂P) = V_m T_g Δα / ΔC_p

where ΔC_p and Δα are the discontinuity in specific heat and coefficient of thermal expansion at the glass transition temperature. For most polymers, ΔC_p is in the range of 0.2 - 0.3 J/(g-K).