Thermal Transitions

Fundamental Thermodynamic Relationships

A first-order transition is defined as a discontinuity in the first derivative of the Gibbs free energy (G). The Gibbs free energy can be expressed in differential form as a function of temperature and pressure, G(T,P):

dG = -S dT + Vdp

where S is the molar entropy and V is the molar volume.

The free energy can be differentiated with respect to temperature at constant pressure,

(∂G / ∂T)_p = -S

or with respect to pressure at constant temperature,

(∂G / ∂p)_T = V

This means a first-order phase transition (such as melting of a polymer) occurs as a discontinuity in volume (p = const) or as a discontinuity in entropy (T = const). The first can be observed as a discontinuity in density (or molar volume) and the latter as a discontinuity in enthalpy. Since the temperature does not change (p = const), the heat capacity C_p is infinite at this transition point.

    

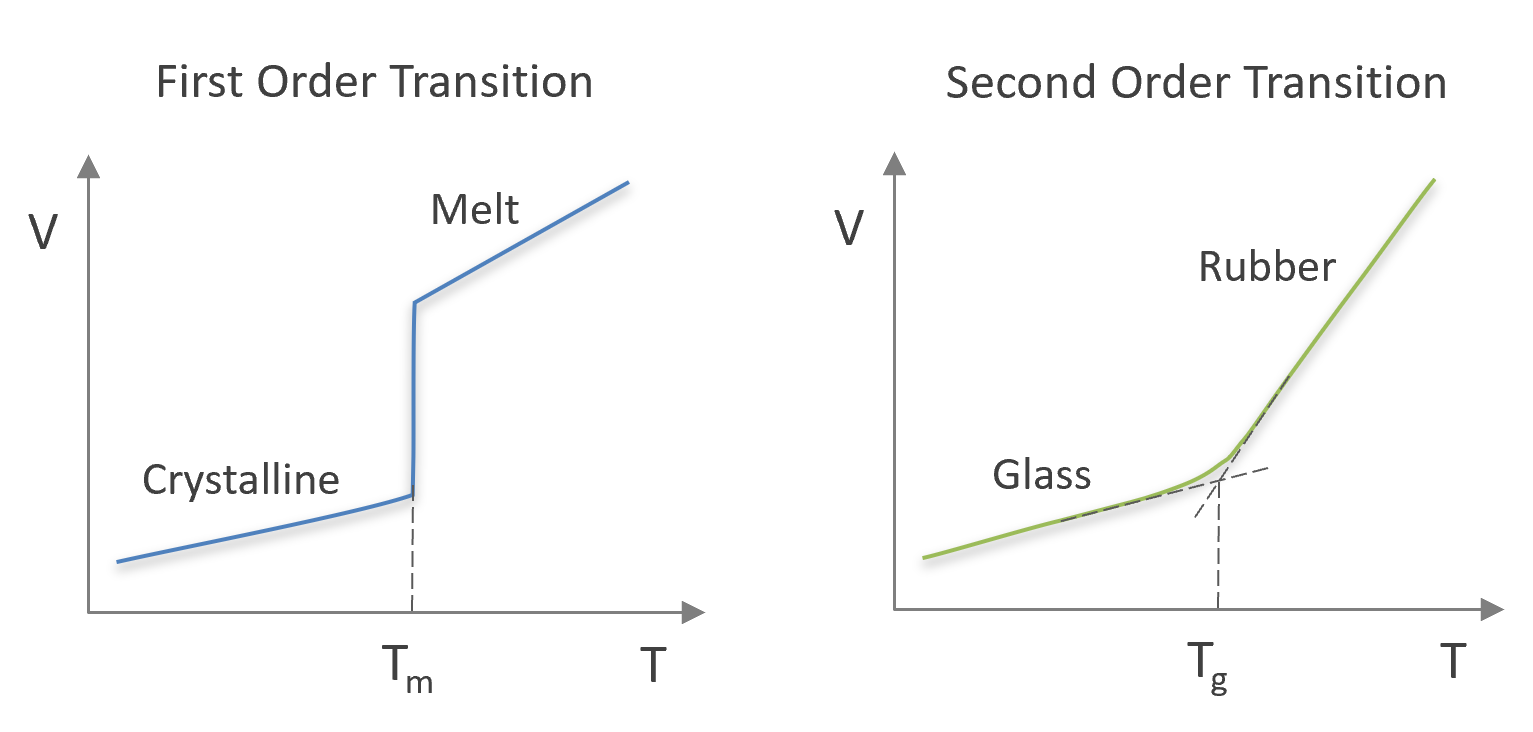
Second-Order Transitions

The glass transtition can be considered an Ehrenfest second-order transition, that is, the discontinuity is only observed in the second derivatives of the Gibbs free energy but not in the first derivatives:

(∂²G / ∂T²)_p = (∂S / ∂T)_p = C_p / T

(∂²G / ∂P²)_T = (∂V / ∂P)_T = -V β

This means, if the glass transition is an ideal second-order transition, both the heat capacity C_p and the isothermal compressibility β (and the volumetric thermal expansion α) change abruptly when the temperature reaches the glass transition temperature. However, for real polymeric systems, the change of these properties, that is the discontinuity or slope, is more gradual and is also affected by the heating rate, i.e. the glass transition is not a true thermodynamic transition but rather a pseudo-second-order transition.