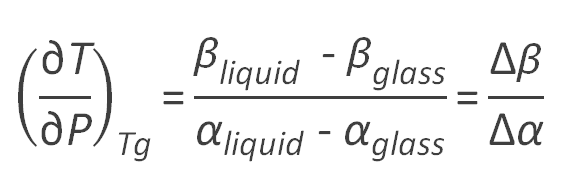Volume Continuity
(Temperature-Pressure Differential at Tg)
At the glass transition, a two-phase equilibrium exist between the liquid and glass phase. Due to volume continuity at the glass-liquid boundary, the pure-component molar volumes in the liquid (rubbery) and glassy state must be identical:
dVglass(T,p) = dVliquid(T,p)
and
Vglass(T,p) = Vliquid(T,p)
At equilibrium, the pressure and the volume are the same in both phases. Then volume continuity demands
(∂Vglass / ∂T)p dT + (∂Vglass / ∂P)T dP = (∂Vliquid / ∂T)p dT + (∂Vliquid / ∂P)T dP
The temperature and pressure coefficient of the molar volume can be written in terms of volumetric thermal expansion and isothermal compressibility, respectively:
(∂V / ∂T)P = V α
(∂V / ∂P)T = -V β
Thus
Vglass αglass dT + Vglass βglass dP = Vliquid αliquid dT + Vliquid βliquid dP
A two-phase equilibrium of a pure material has only one degree of freedom. Therefore, the temperature and pressure changes are not independent on the glass transition phase boundary. Since Vglass = Vliquid, the differential (∂V / ∂P)T along the glass-liquid boundary is