Viscoelastic Response of Polymers under Constant Stress

When viscoelastic materials are subjected to stress they undergo deformations by molecular rearrangements and by viscoelastic flow. To study these deformations, creep experiments are often conducted. In these experiments, a sample is subjected to an instantaneous load at time t₀ and the strain (creep) is recorded as a function of time at constant temperature.

Crosslinked elastomers (ideal elastic materials) undergo only elastic deformations. The creep under stress of these materials can be described with the one-dimensional Voigt model. The basic equation for the time dependence of strain during creep is given by

σ(t) = σ(t)_Elastic + σ(t)_Viscous = E · ε + η · dε / dt

or

σ(t) / η =  dε / dt + ε(t) / λ

where λ is the response or relaxation time of the one-dimensional Voigt element which is represented by the ratio of viscosity η to Young's modulus E. To solve this differential equaition we multiply both sides with the integration factor exp(t / λ):

σ(t) e^t/λ / η = dε / dt e^t/λ + ε(t) e^t/λ / λ

or

σ(t) e^t/λ / η = d[ε(t) e^t/λ] / dt

Voigt Model of Creep & Recover

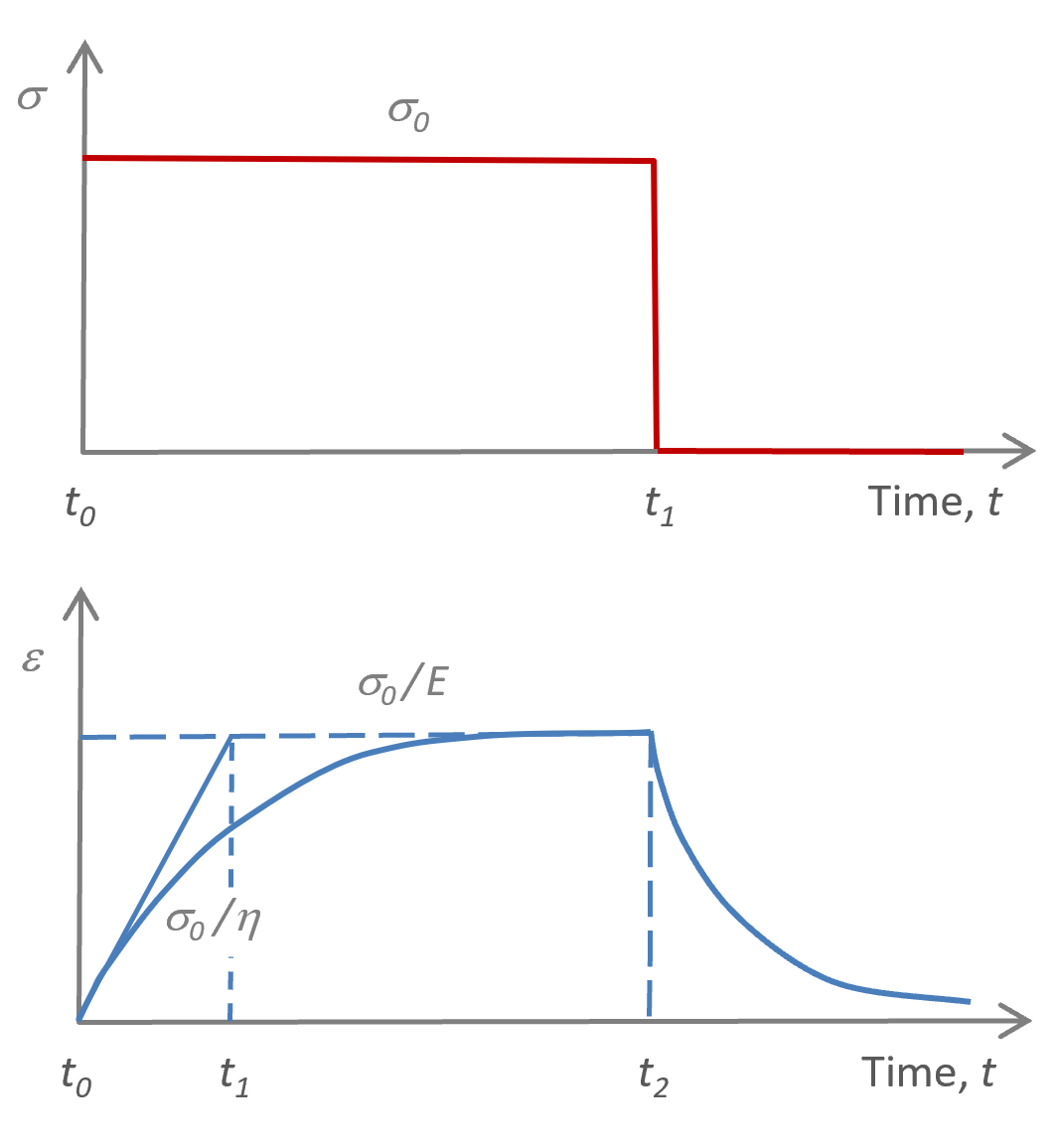
Note, the viscoelastic flow is restricted by the dash-pot in parallel. Hence, there is not instantaneous strain when stress is applied at the start of the experiment at t₀. Assuming ε(t₀) = 0, integration of the equation above yields

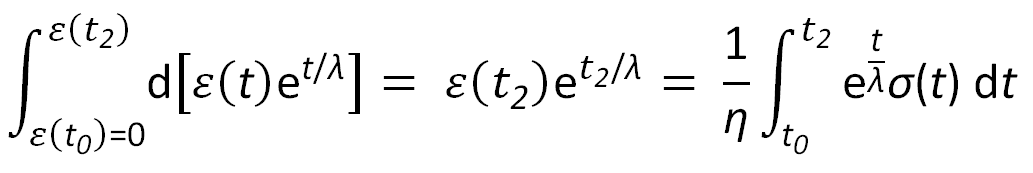
Assuming constant stress, σ(t ≥ t₀) = σ₀, the integral on the right-hand-side can be easily solved:

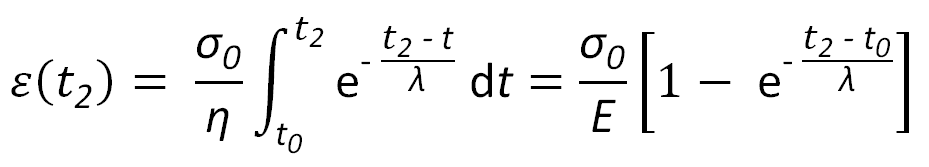
Hence, the strain ε(t) reaches the asymptotic limit σ₀ / E when t → ∞ which is the equlibrium extension of the elastic element. The equilibrium time depends on the temperature; when the temperature increases the relaxation time decreases and the asymptotic limit is reached faster.

Plastic materials undergo irreversible deformation when exposed to stress. This situation can be best described with the one-dimensional Maxwell model. If a constant stress σ₀ is applied then the Maxwell element reaches following strain:

σ₀ = η (dε / dt)  ⇒

ε(t) =  σ₀ {1 / E + t / η}

Maxwell Model of Creep & Recovery

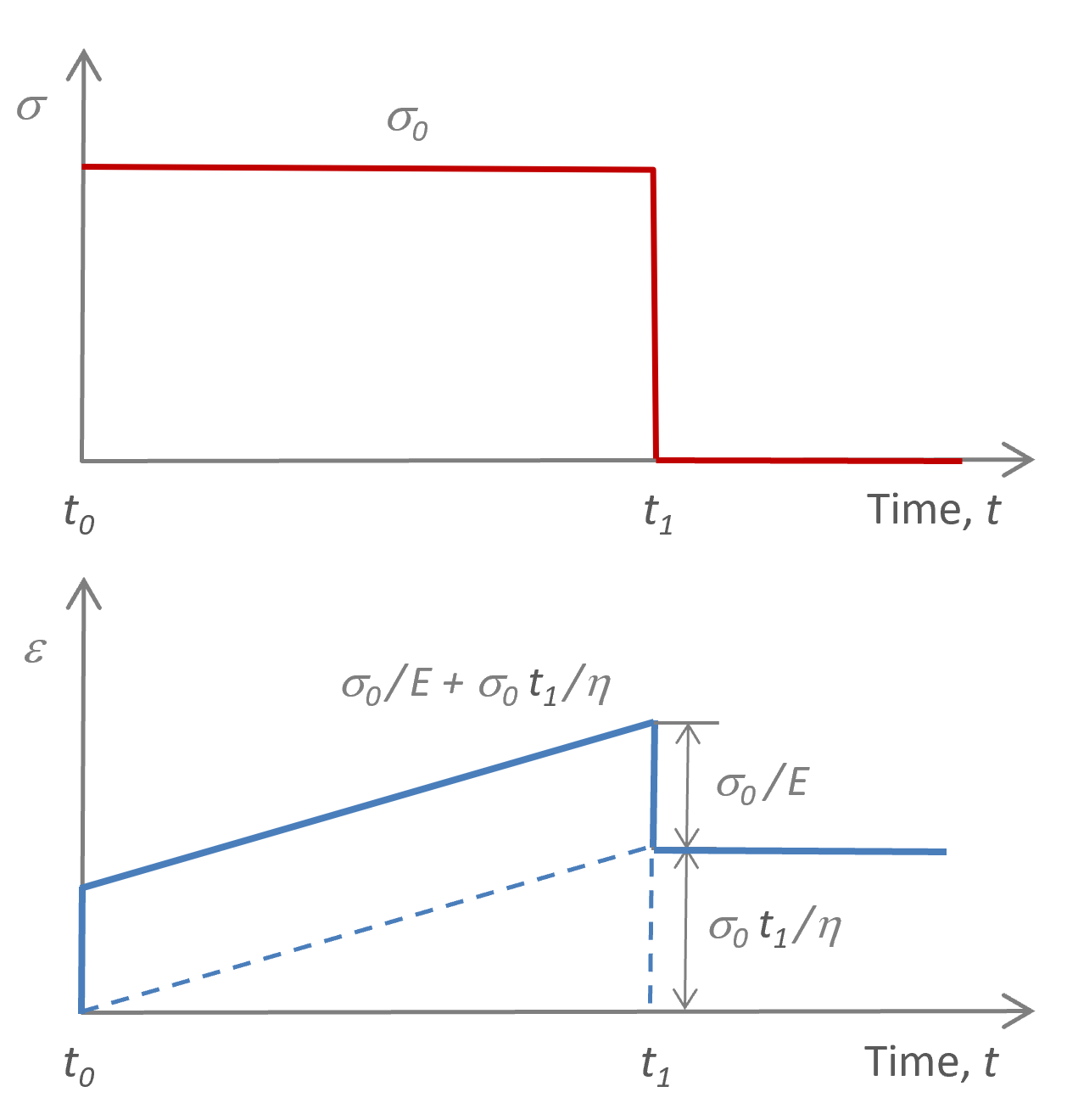
The initial response is identical with the response of the spring, because the movement of the spring in the Maxwell element is not restricted by the dash-pot in series. Thus

ε(t = 0) =  σ₀ / E

The dash-pot simulates the liquid-like behavior at large observation times. After the stress is removed, the spring of the Maxwell element recovers instantaneously but the dash-pot remains at its final position which represent the viscous flow of the material.

ε(t₁) =  σ₀ t₁ / η

This behavior is typical for amorphous polymers without chemical crosslinks which exhibit viscous flow (chain slippage) when exposed to stress.

The viscoelastic behavior of real polymeric materials is usually more complicated. To accurately describe the creep behavior of these materials, Maxwell and Voigt elements have to be combined to more complex arrangments.

References & Further Readings

1. A.D. Drozdov, Viscoelastic Structures. Academic Press, New York, 1998
2. L.H. Sperling, Introduction to Physical Polymer Science, New York, 1992
3. Robert O. Ebewele, Polymer Science and Technology, CRC Press, Boca Raton, Florida 2000
4. F. Mainardi and G. Spada, Eur. Phys. J., Spec. Topics, 193(1), pp 133-160 (2011)
5. D. Roylance, Engineering Viscoelasticity, Dept. Mat. Sci. & Engrg., MIT, 2001
6. W.N. Findley, J.S. Lai, & K. Onaran, Creep and Relaxation of Nonlinear Viscoelastic Materials, Dover, New York, 1989