Maxwell and Voigt Elements

When polymers are subjected to stress, they undergo microscopic and macroscopic deformations by conformational changes (i.e. smaller and larger-scale molecular rearrangements) and by viscoelastic flow. To analyze the viscoelastic response in creep and relaxation experiments, both elastomeric and plastic materials are often modeled by combinations of spring and dashpot elements. The spring behaves exactly like a metal spring, stretching instantaneously under stress and holding the load, whereas the plunger immersed in the dashpot filled with a Newtonina liquid moves at a rate proportional to the stress. On removing the stress, there is no recovery. The ideal spring obeys Hooke's law (σ = E · ε) and the liquid in the dashpot obeys Newton's law of viscosity: σ = η · dε / dt.

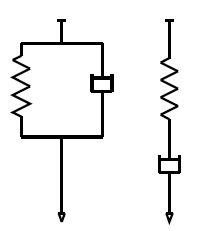
The two simplest arrangements of dashpots and springs are the Voigt and the Maxwell configuration, shown in the figure above. The former is also sometimes refered to as Kelvin or Kelvin-Voigt model. In the Maxwell configuration, both the spring and the dashpot are connected in series. In this configuration, both elements are subjected to the same stress, but are permitted an independent strain. This model is also known as an iso-stress model

σD = σS
εtot = εD + εS

where the subscript D indicates the damper and the subscript S indicates the spring. The basic equation for strain rate in the Maxwell model is

dε / dt = 1/E · dσ / dt + σ / η

In the Voigt configuration, the two elements are connected in parallel and both elements are subjected to the same strain but different stress:

σtot = σD + σS
εD = εS

Because of equal strain in both elememts, the model is also known as an iso-strain model. The basic equation for the stress in the Kelvin-Voigt model is

σ = E · ε + η · dε / dt

The two configurations of dashpots and springs behave very differently in a creep experiment. In this experiment, a stress is applied to the ends of the elements and the strain (creep) is observed as a function of time. The viscoelastic response of the two models are shown below.

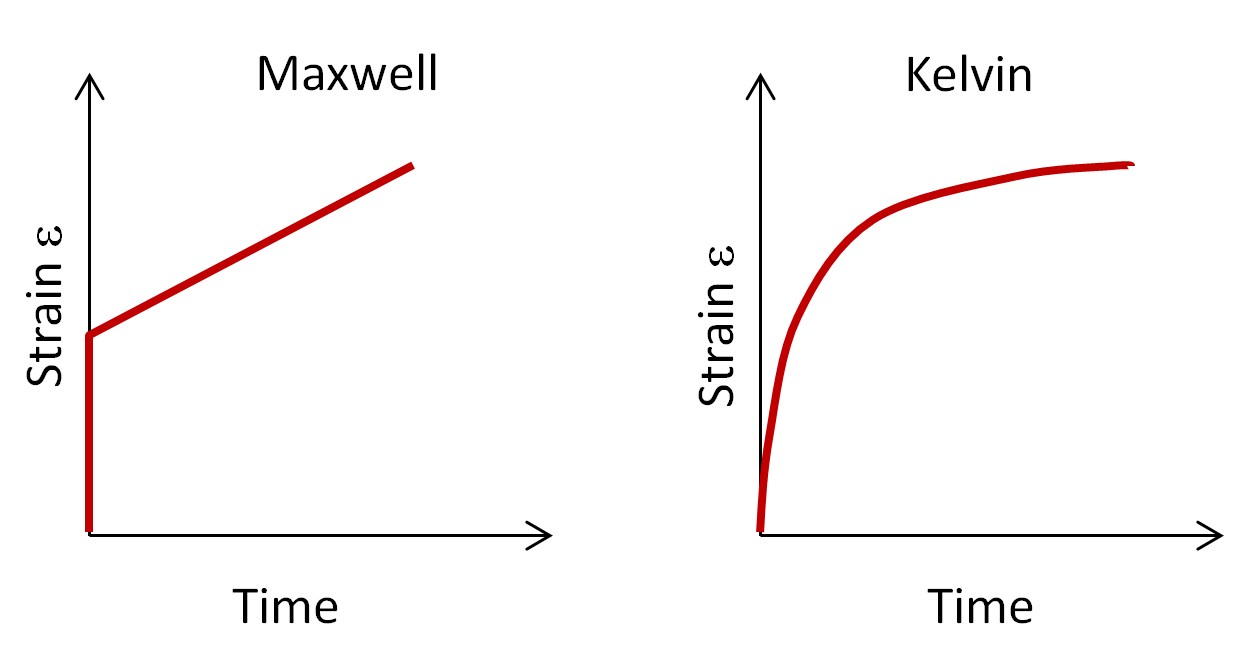
The spring of the Maxwell arrangement response immediately, as illustrated by the vertical line in the graph above on the left. The height of the jump is

ε0 = σ0 / E

While the spring remains at a constant extension or strain, the plunger of the dashpot pulls out at a constant rate. The rate of strain is given by

dε / dt = σ0 / η

Therefore, the effect of a sudden stress is

ε(t) = t · σ0 / η + σ0 / E

Herein is t · σ0 / η the irreversible and σ0 / E the reversible strain response. The initial response is identical with the response of the spring, because the movement of the spring in the Maxwell element is not restricted by the dash-pot in series, while the dash-pot simulates the liquid-like behavior at large observation times.

The Voigt model shows a very different behavior. Since the dashpot and the spring are parallel, the strain in each component are identical. In this configuration, the dashpot reacts very slowly bearing all the stress initially and gradually transferring it to the spring. The differential equation for creep deformation is

σ0 / η = ε / λ + dε / dt

With λ = η / E. This linear differential equation has the solution:

ε(t) = σ0 / E · [1 - exp(-t / λ)]

Some simple viscoelasticity problems can be solved, in first approximation, with the Maxwell and Kelvin-Voigt arrangements alone. However, more often they are combined to more complex arrangments to more accurately describe the creep and relaxation behavior of polymeric materials.

References & Further Readings

  1. David Roylance, Engineering Viscoelasticity. Cambridge, MA 02139: Massachusetts
    Institute of Technology (2001)

  2. L.H. Sperling, Introduction to Physical Polymer Science, 2nd Edition (1992)
  3. F. Mainardi and G. Spada, Eur. Phys. J. Spec. Top., vol. 193, pp. 133–160 (2011)
  4. Julian Vincent, Structural Biomaterials, 3rd Ed., Princeton Univ. Press, 2012
  5. H.T. Banks, S.H. Hu and Z.R. Kenz, Adv. Appl. Math. Mech., 3, pp. 1-51 (2011)

  • Summary

    Viscoelasticity

    To simulate the viscoelastic behavior of polymers, spring and dashpot elements are frequently used.

  • Each spring element obeys Hooke's law: σ = E · ε,
    and each liquid in a dashpot obeys Newton's law of viscosity: σ = η · dε / dt

  • The two simplest arrangements of dashpots and springs are the Kelvin-Voigt and the Maxwell configuration:

    In the Maxwell configuration, the spring and the dashpot are connected in series and both are subjected to the same stress but are permitted independent strains.

    In the Kelvin-Voigt configuration, the two elements are connected in parallel and both elements are subjected to the same strain but different stress.

  • Most polymeric materials do not exhibit viscoelastic behavior described by the simple Maxwell and Voigt models. For these materials, more elaborate spring-dashpot arrangements have to be used to effectively describe their mechanical behavior.