The Wiechert Models

Most polymers do not exhibit viscoelastic behavior described by the simple Maxwell and Kelvin model because the conformational changes and the viscous flow are constrained by a multitude of physical entanglements and chemical crosslinks. Each of these entangled strands relaxes with a different relaxation time depending on its length and structure. In other words, shorter strands relax much faster than longer ones, which leads to a distribution of relaxation times and a relaxation response that spreads over a much longer time than that of a uniform polymer network. For these materials, more elaborate spring-dashpot models have to be employed to effectively describe their complex viscoelastic behavior. A very popular model is the Wiechert model which is made up of a large (arbitary) number of spring-dashpot systems either in parallel or in series as depicted below. Each of these elements represent entanglement strands of different length with different relaxation behavior.

  

Maxwell-Wiechert Models

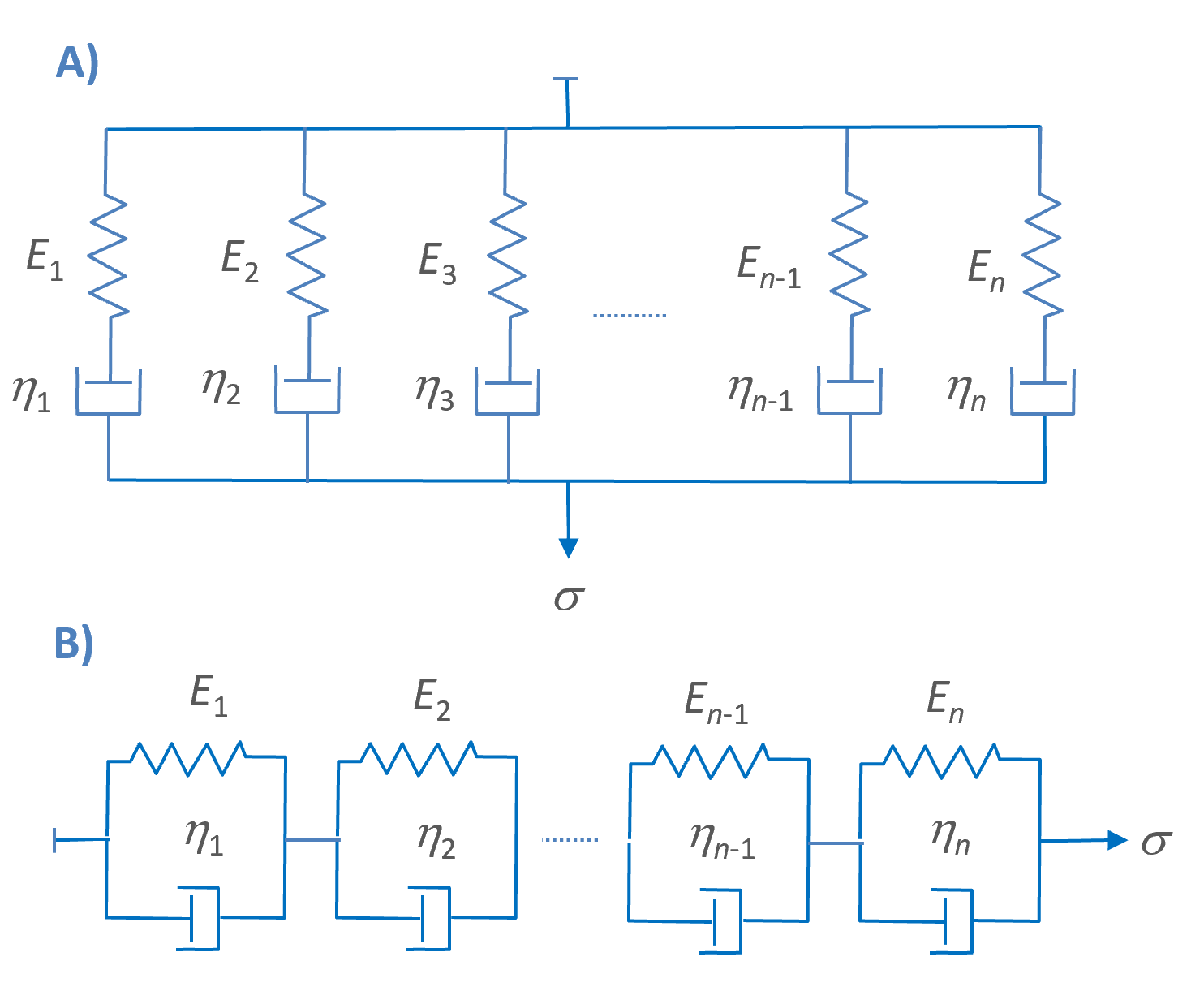
The spring-dashpot systems can be either Maxwell elements in parallel (A) or Voigt elements in series (B). These two models are known as the Maxwell-Wiechert and Voigt-Wiechert model, respectively.¹ Often a single spring in parallel or series to the other elements is placed which describes the ideal elastic response of the material.

Maxwell-Wiechert Model

The Maxwell-Wiechert model is often chosen when the viscoelastic response to strain over a long time period is investigated.² In this model, the strain in the n Maxwell elements is the same, and the total stress is the sum of the stress in each branch:

ε_tot = ε₁ = ε₂ = ... = ε_n-1 = ε_n
σ_tot = σ₁ + σ₂ + ... + σ_n-1 + σ_n

In a stress relaxation experiment, the stress in each individual Maxwell element relaxes exponentially over time:^a

σ_i(t) = σ_0,i e^-t/τ_i

Assuming constant strain (ε₀ = const.), this equation can be rewritten as:

σ_i(t) = ε₀ E_i e^-t/τ_i

where τ_i = η_i / E_i is the response or relaxation time of an individual one-dimensional Maxwell element and E_i and η_i are the modulus of an individual spring and the viscosity of the fluid in an individual dashpot, respectively.

The total stress transmitted by the Wiechert model is equal to the sum of stress in each of the Maxwell spring-dashpot branches:

σ_tot(t) = σ_s + ε₀ ∑_i E_i e^-t/τ_i

or

E(t) = E_s + ∑_i E_i e^-t/τ_i

where σ_s and E_s are the stress and Modulus of the isolated spring which describes the ideal stress response of the material. If the number of Maxwell elements is very large (n → ∞) , the summation in the equation may be replaced by an integral over a continuous distribution of relaxation times τ:

E(t) = E_s + ∫ E(τ) e^-t/τ dτ

If the spring were removed, then the stress in the Maxwell-Wiechert model would decay to zero rather than to a finite value which describes the viscoelastic behavior of a thermoplastic.

Voigt-Wiechert Model

If stress, rather than strain is applied, a series arrangement of Voigt elements is preferred to describe the viscoelastric response of a plastic over a long time period. Often a spring in series is added, which describes the instantaneous elastic response of the material. In this model, the stress in the n Voigt elements is the same, and the total strain is the sum of the strain in each element:

ε_tot = ε₁ + ε₂ + ... + ε_n-1 + ε_n
σ_tot = σ₁ = σ₂ = ... = σ_n-1 = σ_n

Assuming constant stress (σ₀ = const.), the strain response in each individual element is given by:^b

ε_i(t) = J_i σ₀ · (1 - e^-t/τ_i)

where J_i = 1/E_i is the compliance. The total strain response of the Voigt-Wiechert model is equal to the sum of strains in each of the Voigt elements:

ε_tot(t) = ε_s + σ₀ ∑_i J_i (1 - e^-t/τ_i)

or

J_tot(t) = J_s + ∑_i J_i (1 - e^-t/τ_i)

where ε_s and J_s are the strain and compliance of the isolated spring which describes the ideal strain response of the material. If the number of Voigt elements is very large (n → ∞), the summation in the equation above may be replaced by an integral over a continuous distribution of relaxation times τ:

J(t) = J_s + ∫ J(τ) (1 - e^-t/τ) dτ

where J(τ) is a continuous distribution of compliances. The Voigt-Wiechert model above describes an elastic material without permanent deformation. In the case of a thermoplastic or viscoelastic liquid, a dashpot in series has to be included. This element describes the irreversible deformation of the viscoelastic material.

Notes & Further Readings

1. The two models are also known as generalized Maxwell and generalized Voigt(-Kelvin) models.
2. Stress relaxation is a gradual reduction in stress with time at constant strain.
3. F. Mainardi and G. Spada, Eur. Phys. J., Spec. Topics, 193(1), pp 133-160 (2011)

4. W.N. Findley, J.S. Lai, & K. Onaran, Creep and Relaxation of Nonlinear Viscoelastic Materials, North-Holland Publ. Comp., Oxford 1976

5. D. Roylance, Engineering Viscoelasticity, Dept. Mat. Sci. & Engrg., MIT, 2001
6. Rois bert O. Ebewele, Polymer Science and Technology, CRC Press, Boca Raton, Florida 2000
7. A.D. Drozdov, Viscoelastic Structures. Academic Press, New York, 1998
8. L.H. Sperling, Introduction to Physical Polymer Science, New York, 1992