Barton and Johnston Equation
For Copolymer Glass Transition Temperature

A number of semi-empirical equations have been proposed to predict the glass transition temperature (T_g) of a copolymer from its overall composition and the T_g's of the corresponding homopolymers of the monomers. Two of the earliest models that include the monomer arrangement or sequence distribution in the prediction were proposed by Barton and Johnston.^1,2 Although different in detail, both models predict very similar glass transition temperatures for copolymers which are in excellent agreement with published data for numerous copolymer systems.^3,4

Barton’s and Johnston’s model have been called dyad models, because both predict the glass transition temperature from the mass or mole fractions of the monomer dyads found in the copolymer chain. If, for example, a copolymer chain is composed of two types of monomers A and B, four different dyad sequences can be observed: AA, BB, AB, and BA (see figure below).

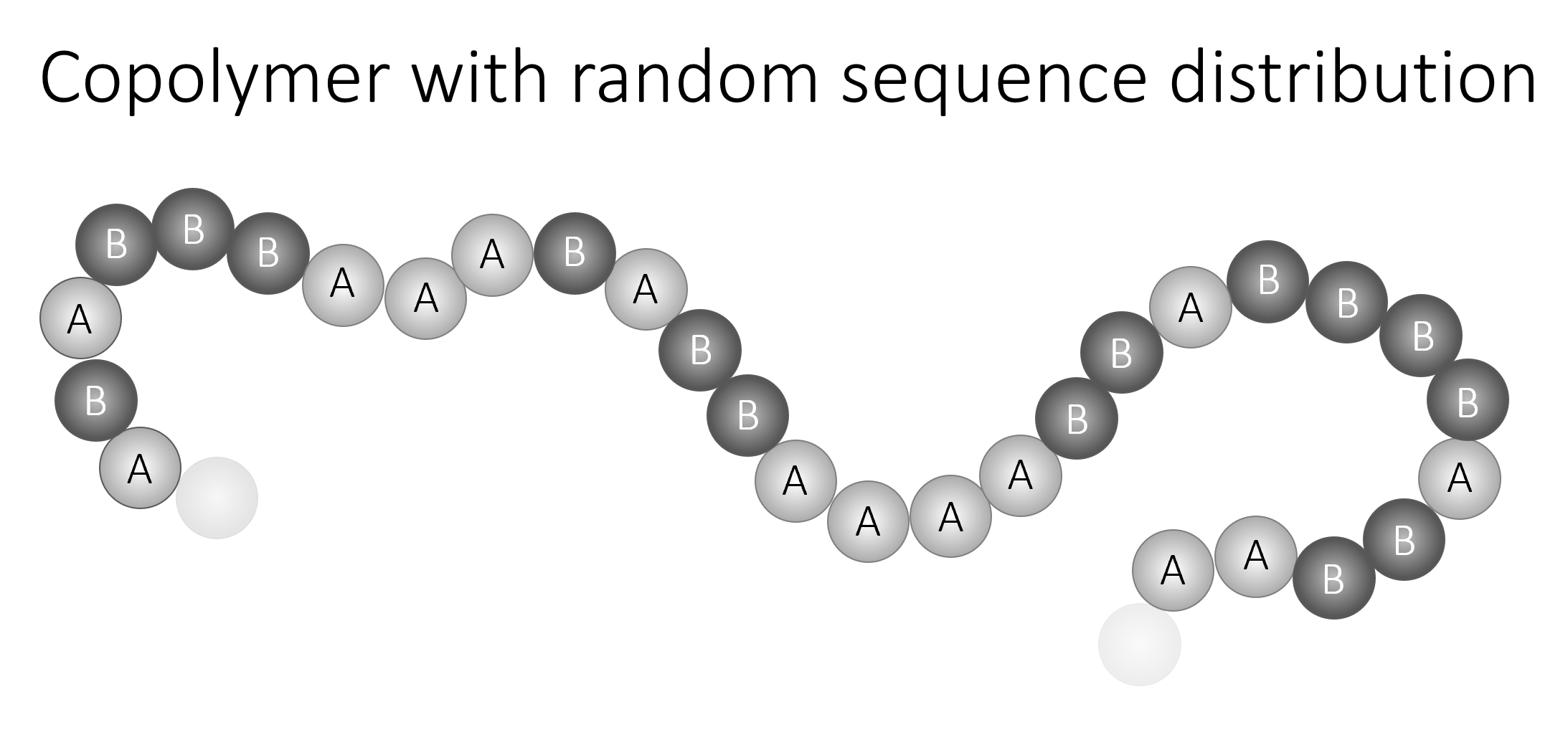
Since AB and BA linkages are chemically equivalent, the number of different linkages in the copolymer chain is only three. These three linkages have generally different stiffness, i.e. different bond length and bond angle vibrations which in turn determine the glass transition temperature. For this reason, Barton postulated that the T_g of a copolymer depends on the mole fractions x_ij of the three different dyads in the AB-copolymer:¹

T_g = x_AA · T_g,A + x_BB · T_g,B + (x_AB + x_BA) · T_g,AB

where T_g,AB is the glass transition temperature of an AB alternating copolymer and x_ij is the mole fraction of an ij dyad sequence. The latter is equal to the product of the mole fraction of i units x_i and the probability P_ij that a given i unit has a j unit on its right, x_ij = x_i P_ij.^3,4

T_g = x_A P_AA T_g,A + x_B P_BB T_g,B + (x_A P_AB + x_B P_BA) · T_g,AB

According to Harwood and Ritchey⁵, the sequence distribution of a copolymer with monomer mole fractions x_A and x_B can be described by a single parameter, the so called run number R, which is the average number of monomer sequences (or runs) found in a copolymer per 100 monomer units. From R the average number of AA, BB and AB dyads can be easily calculated. For example, the mole fraction of A-B linkages is simply x_AB = R / 200, since there are as many A runs as B runs in the copolymer. The number of A-A runs, on the other hand, is equal to the number of A units present in the copolymers minus the number of A-B linkages. Thus, x_AA = x_A - R / 200 and x_BB = x_B - R / 200. With these relations, Barton's equation can be rewritten as^3,4

T_g = x_A · T_g,A + x_B · T_g,B + R / 100 · [T_g,AB - T_g,avg]

with

T_g,avg = (T_g,A + T_g,B) / 2

Johnston chose as a starting point the Fox equation which he extended to²

1 / T_g = ω_A P_AA / T_g,A + ω_B P_BB / T_g,B + (ω_A P_AB + ω_B P_BA) / T_g,AB

where ω_i is the weight fraction of a repeat unit and P_ij is the probability that a given i unit has a j unit on its right (or left). As has been shown by Suszuki and Miyamoto, the equation can can be rewritten in the form^4,6

1 / T_g = ω_A / T_g,A + ω_B  / T_g,B + R / 200M_avg · [(M_A + M_B) / T_g,AB
- M_A /T_g,A - M_B /T_g,B]

with

M_avg = x_A M_A + x_B M_B

where M_i is the formula weight of a repeat unit i. Note, unlike many other models, Johnston's and Barton's models have no adjustable fitting parameters.

To calculate glass transition temperatures for a given copolymer composition, we need to know the monomer sequence or run number R of the copolymer. This parameter can be either determined experimentally, for example from spectroscopic measurements, or it can be estimated indirectly from the following equation⁴

R = 400 x_A x_B / {1 + [1 + 4 x_A x_B (r_Ar_B - 1)]^½}

where r_A and r_B are the monomer reactivity ratios in copolymerization.

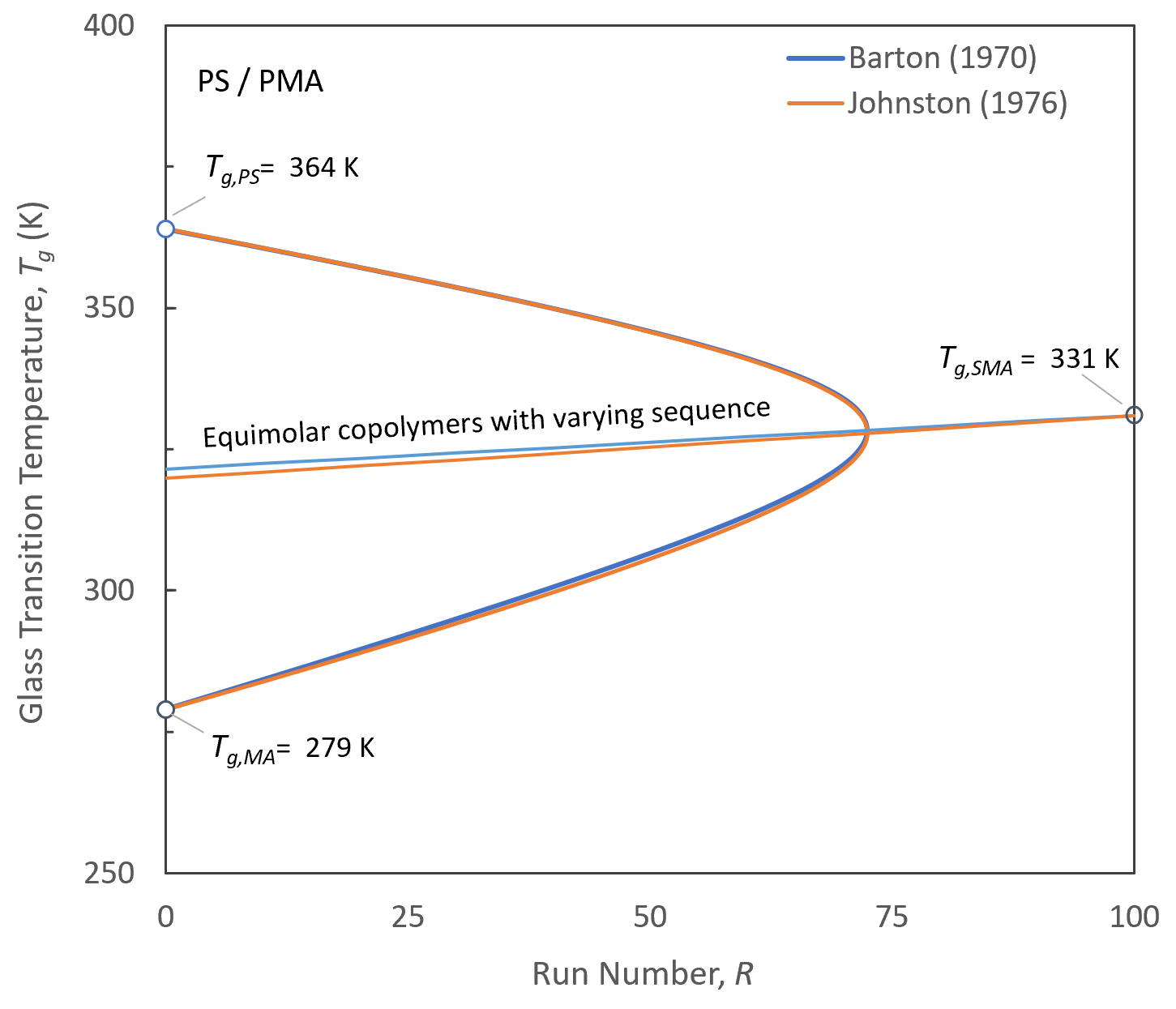
As an example, the figure below shows the Johnston and Barton equation for statistical styrene / methyl acrylate copolymers. The curves have been calculated with the Barton's data: 337.7 K for T_g,S-MA and 0.75 / 0.18 for r_S / r_MA.¹ It can be seen that both equations predict very similar glass transition temperatures.

References & Notes

1. J. M. Barton, J. Polym. Sci., Part C, 30, 573-597 (1970)
2. N. W. Johnston, J. Macromol. Sci. Rev. Macromol. Chem., C14, 215 (1976)
3. H. Suszuki and Y. Muraoka, Bull. Inst. Chem. Res., Kyoto Univ., 67, 2, 47-53 (1989)
4. H. Suzuki and T. Miyamoto, Bull. Inst. Chem. Res., Kyoto Univ., 66, 3, 297-311 (1988)
5. H. J. Harwood and W. M. Ritchey, J. Polym. Sci., B2, 601-607 (1964)
6. Note, Suzuki's expression⁴ reads 1 / T_g = ω_A T_g,A + ... but it should read 1 / T_g = ω_A / T_g,A + ...