Two-Parameter Theory

Polymer Dimension in Dilute Solution

The swelling behavior of polymer chains in solvents was first investigated by Paul Flory in 1949.¹ He developed the first approximate theory describing the expansion of polymer chains in good solvents and showed that the mean square end-to-end distance ⟨R²〉 of a polymer of N links becomes asymptotically proportional to a power of N. In its original form, Flory's theory gives only an approximate solution for the degree of swelling of polymer chains in solvents. It also cannot be considered a theory developed logically from the formalism of statistical mechanics^2-4.

 

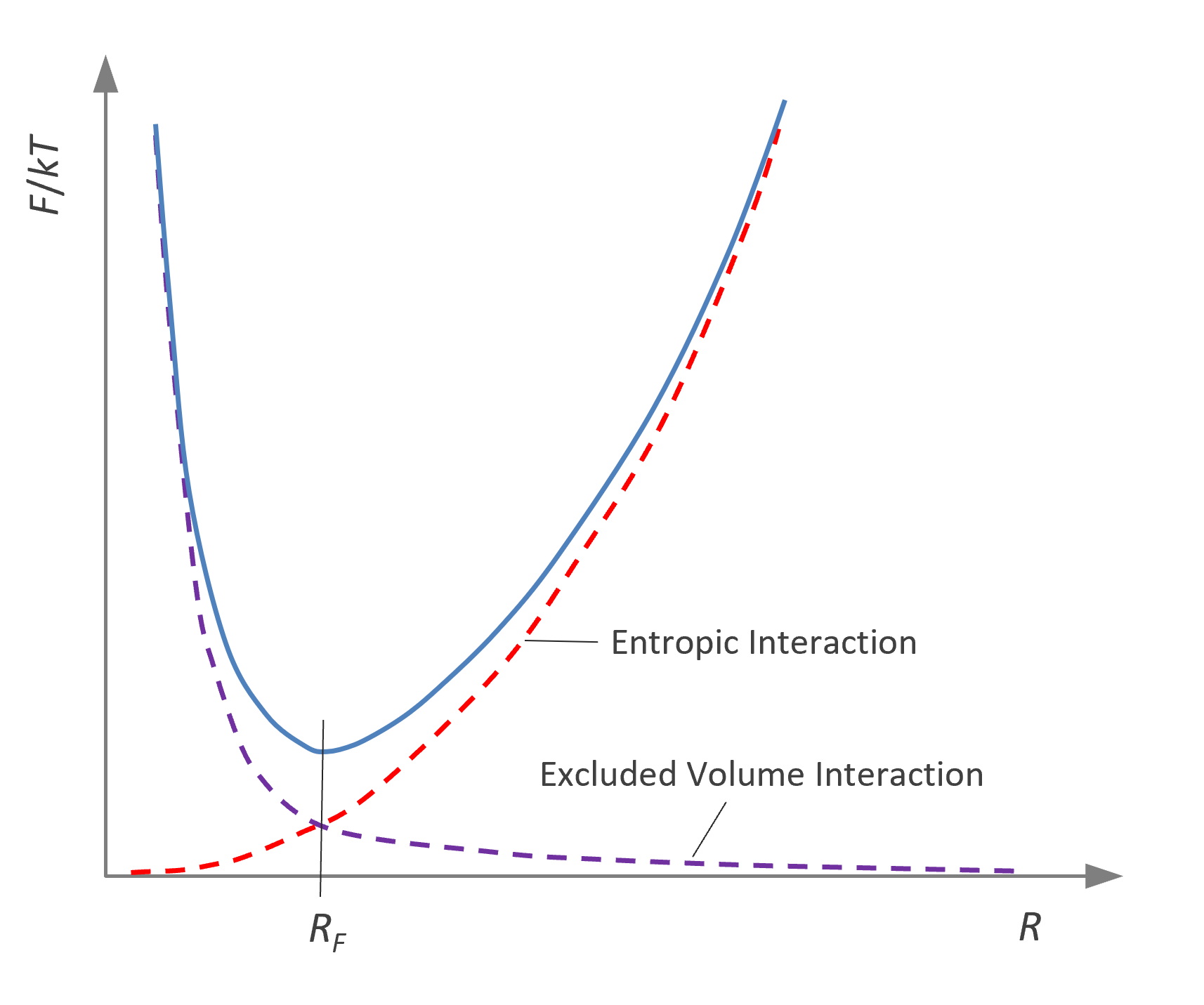
In Flory's treatment, the chain expansion is calculated from the balance between the osmotic pressure, which tends to swell the chain in a good solvent, and the elastic retracting force arising from the coil expansion to a less probable arrangement of bonds.¹ Flory used a mean-field approach to estimate the equilibrium conformation of real polymer chains. According to his theory, the free energy due to the excluded volume is F_ex/kT ≅ (N²/2)v/R³ and the entropy of elastic deformation is F_el/kT ≅ R²/(N l_K²) where l_K is the length of a Kuhn segment. The equilibrium coil size R_F is the most probable value, i.e. the value associated with the free energy minimum. Thus, minimizing the total free energy F_tot = F_ex + F_el with respect to R gives the average coil size:

F_tot/kT ≅ (N²/2) v / R³ + R² / (N l_K²)

∂F_tot / ∂R = 0 ⇒

R_F ≅ B N^3/5 ≈ l_K^2/5 v^1/5 N^3/5

or

R_F  =  (l_KN^1/2) · (N^1/2 v / l_K³)^1/5 ≈ 〈R₀²⟩^1/2 z^1/5

where z is the so called chain interaction parameter, and 〈R₀²⟩^1/2 is the size of an ideal (unperturbed) polymer chain. Theories based on statistical mechanics proved that Flory's prediction R_F ≅ N^3/5 is correct. Today, it is believed that the exponent approaches the value ν = 0.588 ≈ 3/5 asymptotically. This value has been confirmed by several numerical studies.^4,5 The uncertainty is probably less than 0.001. It is remarkable that the expoent is universal, that is, it is independent of the temperature and type of polymer. All other effects such as the interaction between polymer repeat units and solvent molecules as well as those of the microstructure are included in the nonuniversal prefactor z.

Free energy as a function of chain dimension

 

Polymer Dimension in Melt State

In the melt state, the excluded volume can be neglected, meaning the polymer chain has the dimensions of an unperturbed polymer chain. The two nonuniversal parameters that determine the size of a polymer coil are the characteristic ratio C_∞ and the mean-square length of a skeletal unit l_ν. The characteristic ratio C_∞ for a linear polymer chain can be defined as

where the denominator N_ν⟨l_ν²⟩ is the mean-square end-to-end distance of an equivalent random-flight or Gaussian chain. Thus, the smaller the C_∞ value, the more like a random-flight chain is the real polymer chain.

⟨R₀²⟩ = C_∞ N_ν ⟨l_ν²⟩

The skeletal unit l_ν can either be real or virtual skeletal bond which is an elementary rotational unit on the polymer backbone.⁶ In the case of polyethylene, it is identical with the length of a carbon-carbon bond, l_ν = 1.53 or ⟨l_ν²⟩ ≈ 2.53 Ų. The same is true for other saturated vinyl polymers such as polypropylene, polyisobutylene, and polystyrene, whereas in the case of stiff chains, the statistical segment is much larger than a C-C bond and not identical with the length of repeat unit. Two examples are shown below

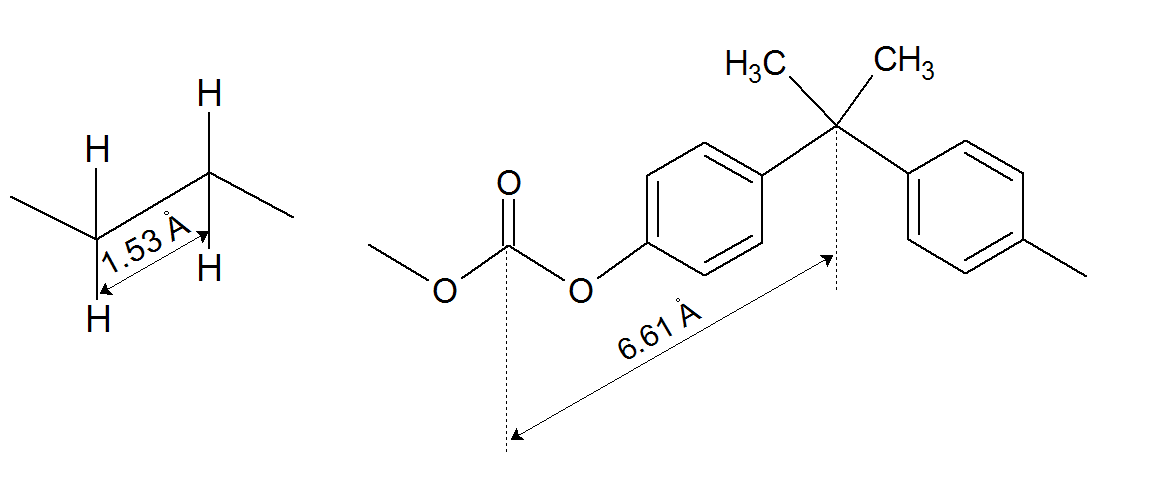
Many other polymer repeat units consist of several bonds of different length and with different rotational potentials. The size of these repeat units is not fixed, but depends on the configuration (rotational states). To simplify calculations, the real bonds are often replaced by virtual skeletal bonds. Their statistical length can be calculated from the rotational energy spectrum of the bonds, that is, from the most probable rotational states of the bonds.

References

1. P. J. Flory, J. Chem. Phys. 9, 660 (1941); 10, 51 (1942); 17, 303 (1949)
2. H. Yamakawa, Modern Theory of Polymer Solutions, New York (1971)
3. B.H. Zimm, W.H. Stockmayer and M. Fixamn, J. Chem. Phys. 21, 1716 (1953)
4. T. Ishinabe, J. Chem. Phys. 76, 5589 (1982)
5. J. Mazur, J. Chem. Phys. 38, 1292 (1963)
6. S. Wu, Polymer lnternational, Vol. 29, No. 3, pp. 229 - 247 (1992)