Temperature and Strain Rate Dependence of Tensile Yield Stress

Yielding of glassy plastics is is a visco-plastic deformation that can be describesd with generalized Maxwell and Kelvin Voigt models. The simplest approach uses a single nonlinear Maxwell arrangement consisting of one spring (elastic element) and one dashpot (viscous element) in series with a stress and temperature activated relaxation time.

Both the spring constant and the viscosity of the dashpot depend on the temperature, resulting in lower yield stress with increasing temperature.

There are two cases of yielding, if the amorphous portion is in the rubbery state, the plastic will have a rather low modulus, and the extension at break will be very large. If, on the other hand, the amorphous phase is in the glass state, the modulus will be large and yielding occurs at much larger stresses, depending on the temperature, molecular weight, polydispersity, and morphology (degree of crystallinty and lamellae size).

According to the above model, the total strain (ε_tot) and strain rate (dε_tot / dt) of the viscoelastic deformation can be separated in an elastic (recoverable) and a plastic (unrecoverable) component:

ε_tot = ε_el + ε_vis
dε_tot / dt = dε_el / dt + dε_vis / dt

Assuming relaxation is caused solely by stress-activated processes, the stress and temperature dependence of the plastic flow (yielding) can be described with an Eyring expression:^1-3

dε_vis / dt = dε₀ / dt · exp(-ΔH / kT) · sinh[V σ / kT] = A sinh(B σ)

For large stresses at yield (V σ / kT » 1), sinh(x) ≈ ½ exp(x), this expression reduces to

dε_vis / dt = dε₀ / dt · exp(-ΔH / kT) · ½ · exp[V σ / kT] = A exp(B σ)

And for rather small stresses at yield (V σ / kT « 1) , sinh(x) ≈ (x) it reduces to

dε_vis / dt = dε₀ / dt · exp(-ΔH / kT) · [V σ / kT] = A B σ

where ΔH is the activation enthalpy for stress activated flow of a structural element, V is the activation volume, σ is the stress in the dashpot which is equal to stress in the spring and dε₀ / dt is a reference strain rate. The Eyring relation can also be written in terms of strain rate:

σ / T = k / V · arsinh(ε^*_vis / ε^*₀)

where ε^*₀ = dε₀ / dt · exp(-ΔH / kT) and ε^*_vis = dε_vis / dt

Assuming a linear response for the elastic element (neo-Hookean behavior up to failure⁴), the equation for strain rate can be rewritten in terms of stress (σ):

dε_tot / dt = dε_el / dt + dε_vis / dt = E^-1 dσ / dt + A sinh(B σ)

In a stress relaxation experiment, the total strain is zero:

0 = E^-1 dσ / dt + A sinh(B σ)

This expression can be solved by separation of variables and integration:

σ₀ - σ ≈ ln [1 - C t ] /B

where C is a constant and σ₀ is the reference stress at t = 0.

In the case of a constant strain rate, the plastic is stretched until it starts to yield. For low extensions, the material stretches like an elastic spring, meaning the strain rate in the dashpot is negligible, so that the stress increases proportional to the strain until the elastic limit is reached. Above this limit, the material undergoes both plastic and elastic deformation. At a certain point, the spring ceases to extend and the total strain rate is equal to that of the Eyring dashpot, i.e. the material undergoes strong yielding. Thus

dε / dt ≈ A sinh(B σ)

or

η = σ / (dε / dt) ≈ σ / [A exp(B σ)]

and with the explicit expressions for A and B

η = σ / {dε₀ / dt · exp(-ΔH / kT) · sinh(V σ / 2kT)}

This equation can be rewritten as

η(σ) = η₀ σ  / {σ₀ sinh(σ / σ₀)}

where σ₀ = kT /V is the characteristic or reference stress and η₀ the zero-viscosity at very small stresses

η₀ = σ₀ / (dε₀ / dt) · exp(ΔH / kT)

Treating yielding as a shear stress activated flow has proved to be a quiet successful approach in predicting the time and strain rate dependence of yielding. However, often more complex arrangements of springs and dahspots are chosen to accurately describe yielding.⁶

Yield Stress to Temperature as a function
of Strain Rate for Polycarbonate

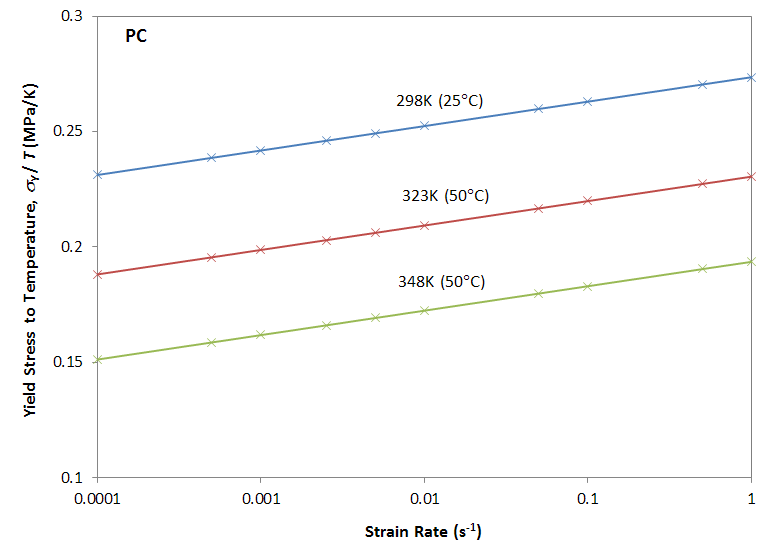
The figure above shows the ratio of yield stress to temperature as a function of strain rate for three different temperatures for polycarbonate. The curves were calculated with ΔH = 300 kJ/mol, V = 3.0 nm³, and dε_o/dt = 1.1 · 10²⁷ s^-1. In agreement with observations, the yield stress decreases with increasing temperature and decreasing strain rate.

References and Notes

1. Ian M. Ward, John Sweeney, Mechanical Properties of Solid Polymers, John Wiley & Sons (2013)

2. R.N. Haward, R.J. Young, The Physics of Glassy Polymers, Springer Science (1997)

3. F. Polo, G. Schwartz, and E.B. Hermida, J. of Appl. Poly. Sci., Vol. 61, 109-117 (1996)

4. It is assumed that the strain hardening contribution caused by molecular orientation under stress is described by a neo-Hookean behavior up to failure)

5. An alternative model is a Hookean spring in series with an Eyring dashpot and another spring in parallel.⁶ In that case, the strain rate is given by³

               dε_vis / dt = dε₀ / dt · exp(-ΔH / kT) · sinh[V (σ-σ_R) / kT]

   where σ_R is the stress of the elastic recovery process before and after yield.

6. R.N. Haward, and G. Thackray, Proc. Roy. Soc., Vol. A302, 453 - 472 (1968)

7. Properties and Behavior of Polymers, Vol 2, John Wiley & Sons (2011)