Rubbery Plateau and Entanglements
When measuring the modulus of a polymer as a function of temperature, a (nearly) constant modulus in the region above the glass transition temperature (Tg) and below the melt (Tm) is often observed which is known as the rubbery plateau. The appearance of a rubbery plateau is the result of entanglements or crosslinks. Both the width of this region as well as the properties in this region depend on the molecular weight between entanglements (Me) or crosslinks. Only polymers that are sufficiently long can form stable, flow restricting entanglements. A good analogy is a bowl of spaghetti. When the individual strands of spaghetti are short, they can be easily separated, whereas long strands are very diffcult to separate from one the other due to the entanglements (knots).
As has been shown by Ferry et al., the rubbery plateau modulus, Gp, is inversely proportional to the molecular weight between two successive entanglements, Me:1
Gp ≅ ρ R T / Me
where Gp is the shear storage modulus of the plateau region at a specific temperature T,
ρ is the polymer density, and R is the ideal gas constant.
An alternative definition based on the tube model has been suggested
by Doi and Edwards:2
Gp ≅ 4/5 · ρ R T / Me
Their model allows for some relaxation in the plateau region.3,4
The rubbery plateau is also related to the degree of crystallinity in a material, that is, the temperature behavior of the modulus of a semicrystalline polymer is qualitativley similar to that of a high molecular weight amorphous polymer, only the modulus is typically higher in the secondary plateau due to the reinforcement effect of the crystalline domains dispersed in the amorphous rubbery phase above the Tg but below the melting point (Tm).
Modulus vs. Temperature
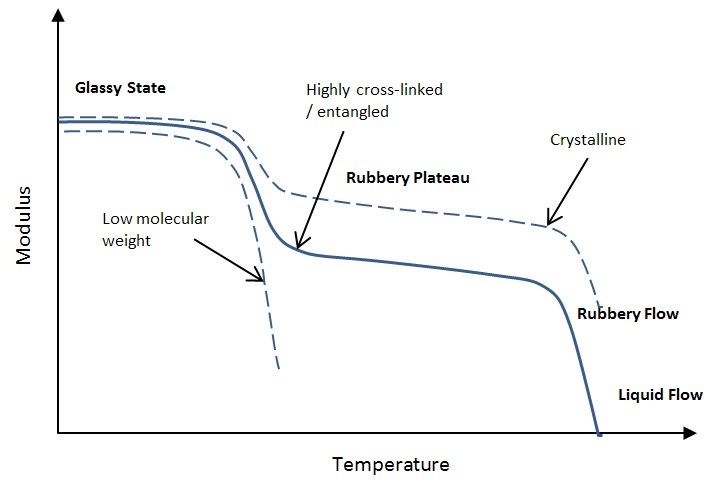
Modulus vs. Temperature
References & Notes
J.D. Ferry, Viscoelastic Properties of Polymers, 3rd Ed., John Wiley, New York 1980
M. Doi & S. F. Edwards, The Theory of Polymer Dynamics, Oxford Univ. Press, New York 1986
In the tube model, the tube diameter, d, is proportional to the average number of entanglements per molecule, Me:
M / Me = L / d
where L is the contour length of a random walk of M / Me steps.T.C.B. McLeish, Advances in Physics, 51, 6, 1379-1527 (2002)