Viscoelastic Response of Polymers under Constant Strain

In plastic materials, prolonged exposure to stress may cause noticeable and irreversible deformation which must be taken into consideration when designing parts for structural applications. The susceptibility to (permanent) deformation under load or relaxation under stress can be measured in creep and stress relaxation experiments, respectively. In the latter case, the test specimen is rapidly strained to a certain extension, and the force required to maintain this constant strain is measured as a function of time.¹

In the simplest case, the relaxation under constant strain can be described with the one-dimensional Maxwell model which consists of a spring and dashpot in series. Its time dependence of stress during relaxation is given by

dε / dt = 1/E · dσ / dt + σ / η

Since the strain is constant, the relation above simplifies to

 1/E · dσ / dt = - σ / η

This is a first-order differential equation which satisfies the boundary condition σ(t = 0) = σ₀ and can be solved by separation of variables and integration:

σ₀(t) = σ₀ e^{-t E / η} = σ₀ e^{-t/ τ}

where τ is the response or relaxation time of the one-dimensional Maxwell element which is represented by the ratio of viscosity η to Young's modulus E. This constant is the time in which the stress relaxes to 1/e or 37 percent of its initial stress value (σ₀). If we divide this equation by the constant strain ε, we get a relation for the time-dependent modulus:

E_r(t) = σ/ε e^{-t E / η} = E₀ e^{-t/ τ}

E_r is called the relaxation modulus. According to this model, an instantaneous strain causes only the spring to initially deform, while the dashpot slowly and gradually relaxes and allows the spring to slowly return to zero deformation. Thus, for times much shorter than the relaxation time, the Maxwell element behaves essentially like a spring, whereas for times much longer than the relaxation time, it behaves like a dashpot.

  

Voigt & Maxwell Model of Stress Relaxation

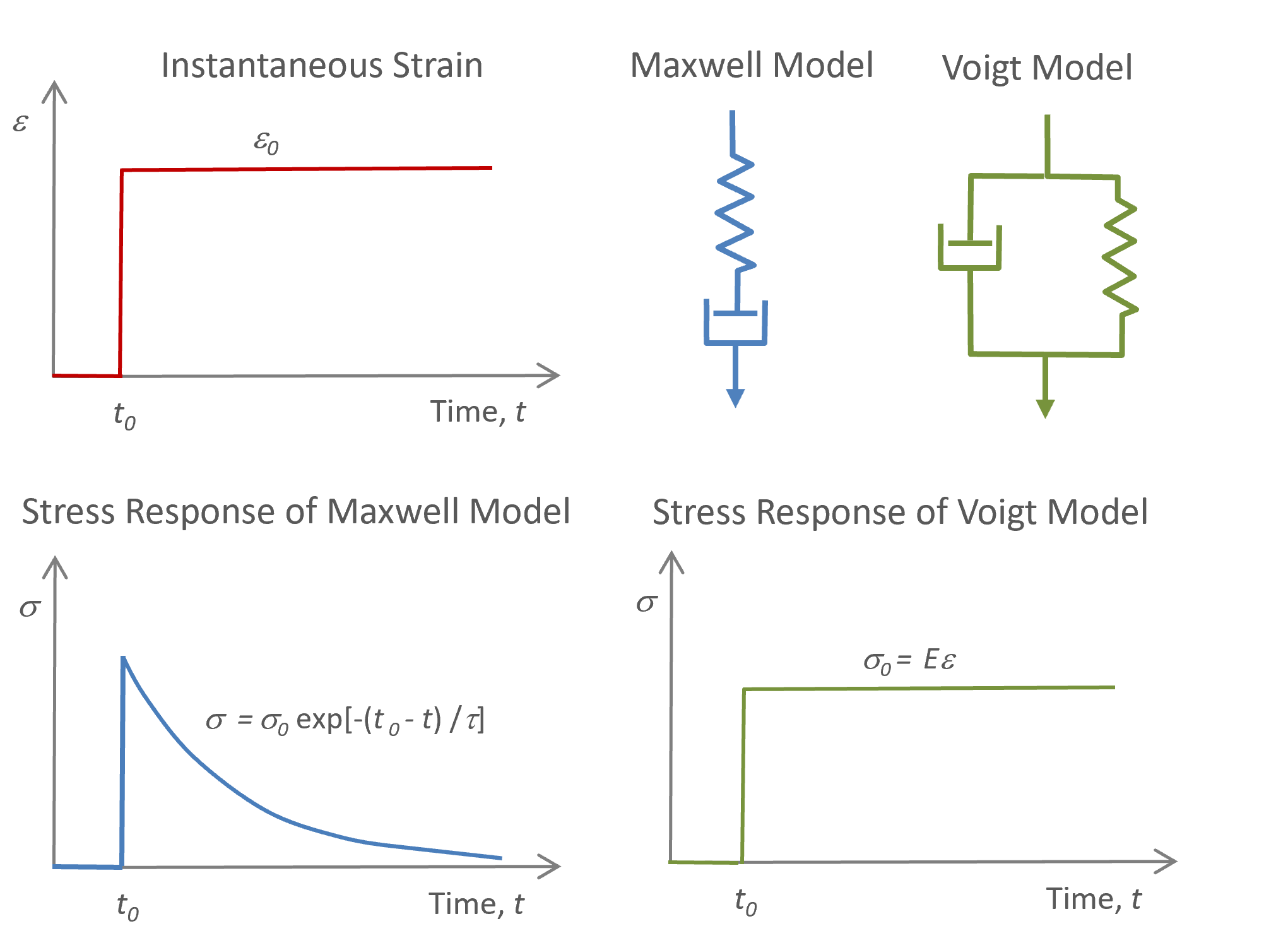
An ideal elastic material, on the other hand, does not experience any relaxation. This material can be described with the Voigt model which consists of a spring paralled to a dash pot. In this arrangement no relaxation takes place because the viscoelastic flow is restricted by the spring. Hence,

ε(t) = ε(t₀) =  σ₀ / E ⇒ σ(t) = σ₀ = E ε

The viscoelastic behavior of real polymeric materials is much more complicated, that is, these materials neither fully relax nor are they ideal elastic. To accurately describe their relaxation behavior, Maxwell and Voigt elements have to be combined to more complex arrangments.

Notes & Further Readings

1. Robert O. Ebewele, Polymer Science and Technology, CRC Press, Boca Raton, Florida 2000
2. Ideally, loading occurs instantaneously whereas in practice, loading always takes place over a finite time. However, for many linear viscoelastic materials, the difference in response is rather small.
3. A.D. Drozdov, Viscoelastic Structures. Academic Press, New York, 1998
4. L.H. Sperling, Introduction to Physical Polymer Science, New York, 1992
5. F. Mainardi and G. Spada, Eur. Phys. J., Spec. Topics, 193(1), pp 133-160 (2011)
6. D. Roylance, Engineering Viscoelasticity, Dept. Mat. Sci. & Engrg., MIT, 2001
7. W.N. Findley, J.S. Lai, & K. Onaran, Creep and Relaxation of Nonlinear Viscoelastic Materials, Dover, New York, 1989