Pearl-Necklace Chain and Excluded Volume

In an athermal solvent¹, a polymer coil will occupy a larger volume than in its melt state. In other words, a real polymer chain will be more expanded than an ideal chain of same length.² This phenomenon is known as the excluded volume effect. The effect was first discovered by Flory in 1949,³ who showed that the average linear dimensions of a polymer chain is proportional to a power of the chain length.

The excluded volume effect can be described with the pearl-necklace model (see Fig. below). In this model, the polymer chain is replaced by a necklace-like chain which is composed of N beads or pearls which represent the excluded volume. The spheres are not allowed to overlap and each bead is always in contact with the two adjacent beads. Thus, the model chain consists of N hard (impenetrable) spheres of diameter 2b and contour length 2Nb.

 

Pearl-Necklace Model of a Polymer

 

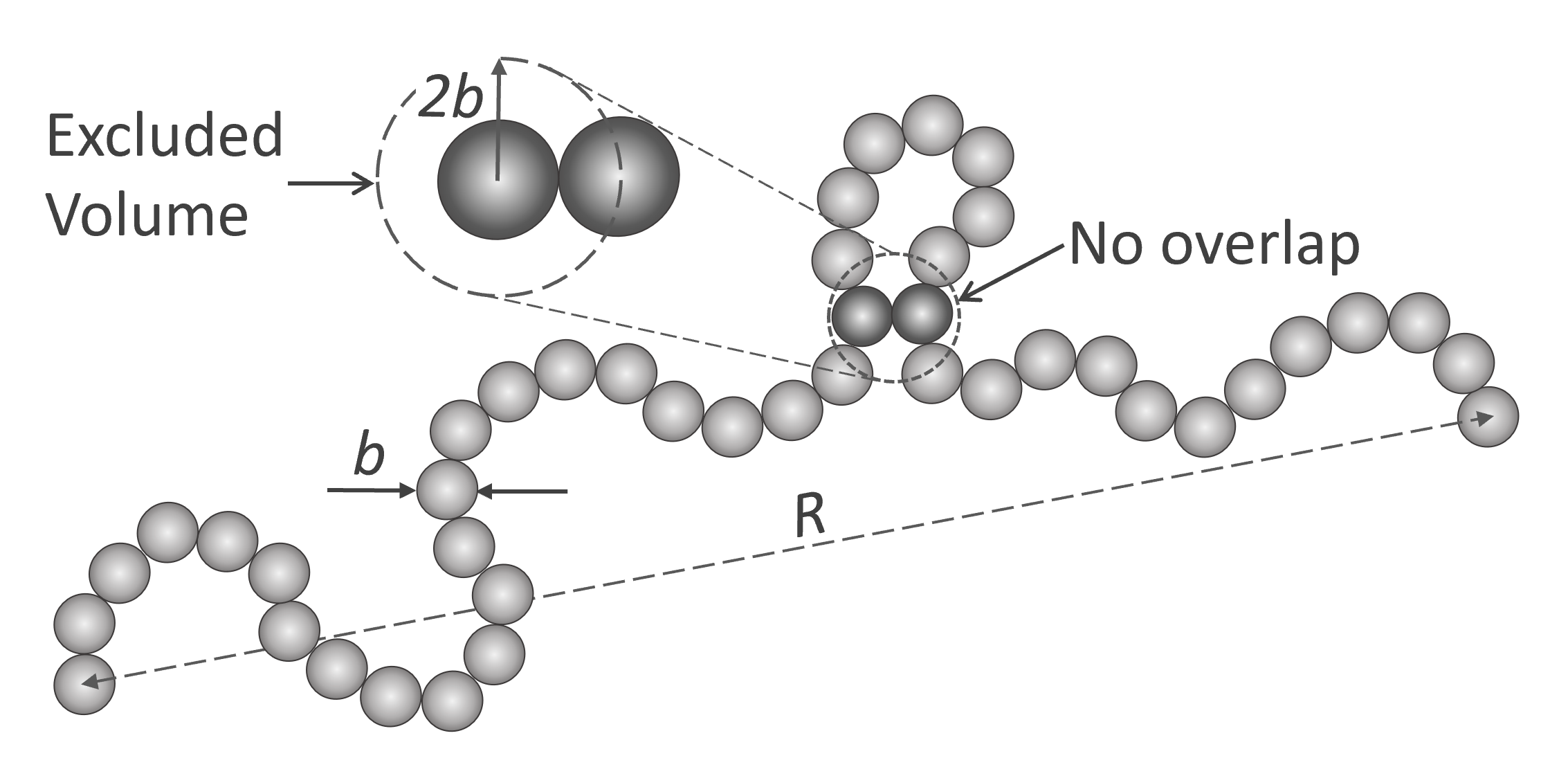
If two nonadjacent beads approach each other, the center-to-center distance between the beads cannot be less than 2b. Meaning the space not available to the center of the approaching bead is a sphere of volume v_excl = 4π/3 (2b)³ (as indicated by the dashed circle). Thus, the excluded volume v_excl is eight times the volume of a bead, v_excl = 8 x v_bead. Then the space available to each bead or pearl decreases from the volume V of the system to V - v_excl and the configurational entropy of each bead changes by

ΔS_bead = k ln[(V - v_excl) /V] ≈ -k v_excl /V

The change in the Helmholtz free energy is given by ΔF/kT = -S/k or

ΔF_bead /kT = ΔS_bead ≈ v_excl /V

A chain of N identical beads has N²/2 possible pairs of excluded-volume interactions. Then, the change in the Helmholtz free energy due to the excluded volume interaction is F_excl /kT = ΔF_bead N²/2kT or

ΔF_excl /kT ≈ (N²/2) v_excl /V = (N²/2) b³/V

In a very dilute solution, each polymer chain can be considered an isolated chain. If such a chain is composed of a very large number of beads, it will resemble a spherical coil with an effective radius R. Flory postulated that all segments of such a chain are confined in this volume.^3,4

 

Pearl-Necklace Chain Confined in a Sphere

 

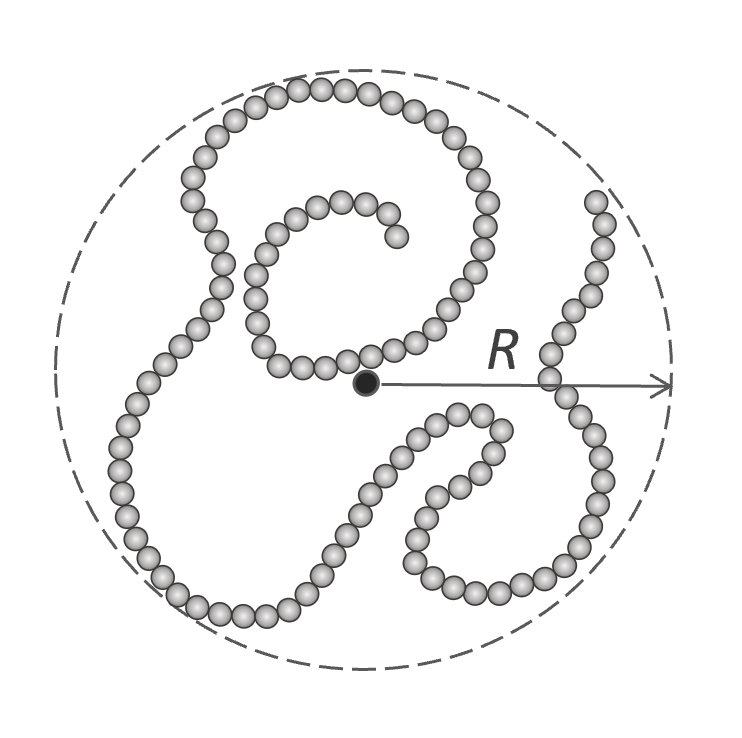
If no other polymer sphere penetrates this volume, the change in free energy per chain due to the excluded volume reads

ΔF_excl(N)/kT ≅ (N²/2) v_excl /R³ ≅ N²b³/R³

where we droped all numerical factors. Since N/R³ is equal to the bead number density ρ_b, and Nb³/R³ to the bead volume fraction in the sphere, the equation above can be rewritten as

ΔF_excl(N)/kT ≅ R³b³ρ_b² = R³/b³φ_b²

The Helmholtz free energy due to excluded volume interaction is only part of the free energy of a polymer coil. A polymer confined within a volume V will also undergo a change in entropy due to loss of degrees of freedom (fewer conformations). Assuming a Gaussian bead distribution, this entropy term is given by ΔF_conf = kTR²/R₀² = kTR²/Nb². Then the total free energy of a confined Gaussian chain can be written as⁵

ΔF_tot /kT = ΔF_conf + ΔF_excl ≅ R²/Nb² + N²b³/R³

The most probable value of R corresponds to the chain with the lowest Helmholtz free energy. Thus, minimizing the total free energy ΔF_tot with respect to R gives the most probable value

 d(ΔF_tot /kT) / dR|_{R = RF} = 0 ⇒ R_F ≅ bN^3/5

Both the elasticity and the excluded volume are entropic in nature. Thus the size of an athermal chain is independent of the temperature.

References & Notes

1. In an athermal solvent, the interactions between solvent and polymer repeat units are equal to those between solvent molecules and polymer segments. Thus, the enthalpy of mixing is zero.

2. A linear flexible polymer chain in its melt state follows Gaussian statistics, i.e. it behaves like an ideal or phantom chain that occupies no volume.

3. P. J. Flory, J. Chem. Phys. 9, 660 (1941); 10, 51 (1942); 17, 303 (1949)

4. Paul Flory, Principles of Polymer Chemistry, Cornell University Press, 1953.

5. M. Rubinstein and R. Colby, Polymer Physics, Oxford University Press, 2003