Couchman-Karasz Equation
One of the most popular equations for predicting glass transition temperatures (Tg) of amorphous mixtures and random copolymers is the Couchman-Karasz equation.(1) This equation is based on the entropy (S) continuity at the Tg:
Sglass(T,p) = Sliq(T,p)
In the case of blends and copolymers, the specific entropy of the mixture at Tg is calculated as a weight-fraction-weighted sum of pure-component entropies, and the change of entropy due to mixing,
Stot(Tg,mix) = ∑i [ωi · Si(Tg,mix) ] + ΔSmixing(Tg,mix)
where Tg,mix is the glass transition temperature of the mixture in the glass or rubber (liquid) state, ωi is the mass fraction of component i, and ΔSmix is the change of entropy due to mixing of the polymer components. It is assumed that the conformational entropy of mixture and that of the components is the same in the liquid and glass state at the glass transition temperature of the mixture, Tg,mix. Hence,
ΔSmix,glass(Tg,mix ) = ΔSmix,liq(Tg,mix )
and
∑i ωi {Si,liq(Tg,mix) - Si,glass(Tg,mix) } = 0
Furthermore, entropy continuity is invoked for each pure component and for the mixture at the glass transtion temperature, Tg,i: Si,glass(Tg,i ) = Si,liq(Tg,i ). The specific entropy changes corresponding to heating the individual components and the mixture are
Si,glass(Tg,mix) = Si,glass(Tg,i) + Cpi,glass ln[Tg,mix/Tg,i]
Si,liq(Tg,mix) = Si,liq(Tg,i) + Cpi,liq ln[Tg,mix/Tg,i]
Entropy continuity for a multicomponent mixture at Tg,mix yields
∑i ωi ΔCp,i ln[Tg,mix /Tg,i] = 0
which upon rearrangement gives
lnTg,mix ≈ ∑i [ωi · ΔCpi ln[Tg,i] ]/ ∑i [ωi · ΔCpi ]
where ΔCpi is the change of the heat capacity when crossing from the glass to the rubber (liquid) state. This is the so called Couchman-Karasz(1) equation for the compositional dependence of the glass transition temperature in miscible multicomponent mixtures via entropy continuity.
The Couchman-Karasz equation has been shown to be very successful for fitting the glass transition temperature of many random copolymers. It can also be used to describe the composition dependence of miscible polymer blends exhibiting negative and positive deviation. However, the Couchman-Karasz equation should not be applied to polymer blends and random copolymers with noticeable specific intermolecular interactions because large deviations from the true Tg of the mixture can be expected.
A suitable example is a blend of polystyrene (PS) and poly(2,6-dimethyl-p-phenylene oxide) (PPO). Both polymers have similar structural groups and no specific interactions are present. The predicted values for such a blend are in excellent agreement with the experimental values (see Figure and Table below).5
.| Weight Fraction PS | Exper. Tg (K) | Predicted Tga (K) | |
| 0 | 489 | 489 | |
| 0.2 | 461 | 459.6 | |
| 0.4 | 434 | 434.8 | |
| 0.5 | 425 | 423.3 | |
| 0.6 | 413 | 412.3 | |
| 0.8 | 396 | 391.7 | |
| 1.0 | 379 | 379 |
Glass Transition Temperature of PS-PPO blends
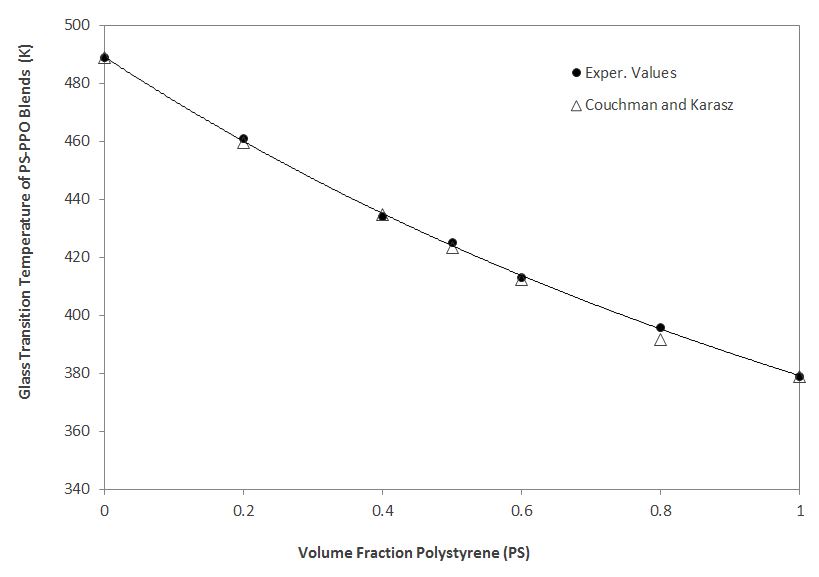
Glass Transition Temperature of PS-PPO blends
References & Notes
-
P. R. Couchman F.E. Karasz, Macromolecules 11, 117–119 (1978)
-
X. Lu and R.A. Weiss, Macromolecules 25, 3242 - 3246 (1992)
-
U. Gaur and B. Wunderlich, J. Phys. Chem. Ref. Data, Vol. 10, No. 4, 1981
-
U. Gaur and B. Wunderlich, J. Phys. Chem. Ref. Data, Vol.11 , No. 2, 1982
-
The values have been calculated with the experimental discontinuos increments in
specific heat, cited by Wunderlich and Gaur in literature 3 and 4