Links:

Surface Properties
of Polymers

One of the most striking demonstrations of intermolecular forces is the tension at the surface of a liquid. The effect of surface tension is seen everywhere; small objects like a metal paper clip that is denser than water does not submerge, and seeds and insects can float or freely move on the water surface.

At the liquid interface, the attractive forces between molecules are mainly in the direction of the bulk and parallel to the surface, whereas there are only little attractive forces between the liquid and the vapor molecules due to the low density of the vapor. The resulting force pulls the liquid towards the center and causes it to contract to form the smallest possible surface.

The surface free energy is defined as the energy required to increase the surface between vapor and liquid by one unit surface, expressed in mJ/m² or erg/cm². The surface free energy is equivalent to a line tension acting in all directions parallel to the surface, which is called surface tension and is usually epressed in mN/m or dyne/cm. The surface tension and surface free energy are numerically and dimensionally identical for liquids but not for all solids because solid surfaces do not necessarily assume an equilibrium shape, thus, the surface energy of a polymer in its solid state can be (much) larger than in its liquid state.
The surface tensions of liquids and solids can not be obtained in the same manner; liquid surface tensions can be directly measured, for example by measuring the force required to pull a metal ring out of a liquid, whereas solid surface tensions have to be derived indirectly, for example from contact-angle measurements using semiempirical equations. In the case of liquids, the measured values are usually independent of the specific technique used, provided an equilibrium between the vapor and liquid is established, whereas the tension of a solid depends on the choice of liquids and equations.

Since the surface tension is caused by intermolecular forces, it is directly related to other physical properties derived from intermolecular forces, such as internal pressure and cohesive energy density (e_coh). According to Hildebrand and Scott (1950) and others a simple relation between surface tension and cohesive energy density exists:

γ_l ≈ A e_coh · V_m^1/3

in which A is a constant and V_m is the molar volume of a molecule or polymer repeat unit. Another simple relation between cohesive energy density and surface tension was suggested by Krevelen.¹ It reads

γ_l ≈ 3/4 e_coh^2/3

Both equations give reasonable estimates for non-polar and polar liquids. However, in the case of hydrogen-bonded liquids large discrepancies between the measured and predicted surface tensions are observed. Koehnen et al.² (1975) postulated that the interactions responsible for liquid-vapor surface energy do not involve the breaking of hydrogen bonds. They suggested following equation:²

γ_l ≈ A (e_polar + e_disp) · V_m^1/3

or expressed in terms of partial solubility parameters

γ_l ≈ A (δ_p² + δ_d²) · V_m^1/3

where e_polar and e_disp are the partial cohesive energy densities due to dipole-dipole and dispersion forces. Koehnen et al. tested this relation for a large number of liquids and found that it fits practically all substances with a correlation coefficient of 0.99.

The surface tension can also be estimated with the molar parachor. This quantity was first introduced by Sugden (1924), who gave a list of atomic and group contributions which was slightly modified and improved by Mumford (1929) and by Quayle (1953):^3,4

[P] = γ_l^1/4 M / ρ = γ_l^1/4 V_m

The parachor [P] is practically independent of temperature and, therefore, can also be used to calculate the temperatur dependence of the surface tension.

 

Predicted vs. Exper. Surface Tension of Polymers

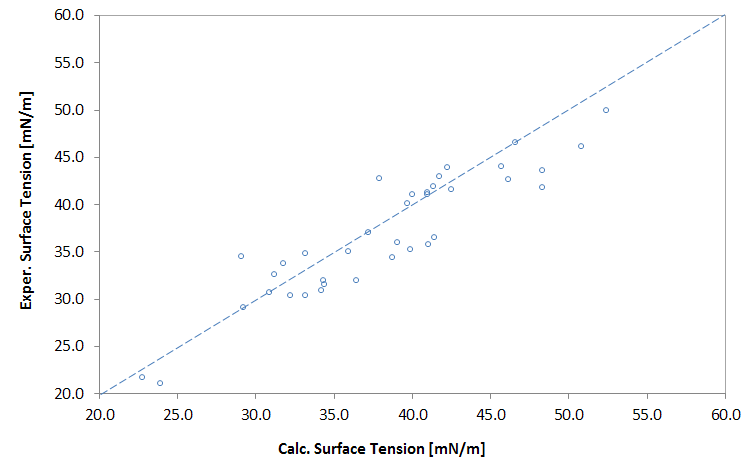
The surface tension of polymers is usually a function of molecular weight. This is most apparent at low molecular weight where the molecular weight and the end-groups have a noticeable effect on the density and composition, whereas for high molecular weight polymers this effect can be neglected. Luckily, the surface tension of low molecular weight polymers can be extrapolated to infinite molecular weight. As Wu⁵ has shown, the dependency of the surface tension on the (number-average) molecular weight M_n can be described with

γ_lv = γ_∞ K_e / M_n^2/3

where γ_∞ is the surface tension at infinite molecular weight and γ_lv the surface tension at a number average molecular weight M_n. K is a constant which depends on the type of polymer. Its value is often in the range of 300 to 400. Wu⁵ has given an alternative equation:

γ_lv^1/4 = γ_∞^1/4 - K_s / M_n

Both equations usually fit the experimental data equally well.

Sauer and Dee (1994) have shown that a M_n^2/3 dependence is more appropriate for lower molecular weights, whereas for high molecular weights a M_n^-1 dependence gives better fits. Nevertheless, the difference in surface tension for low and high molecular weight is rather small and does usually not exceed 2 mN/m.

References

1. D.W. van Krevelen and K. te Nijenhuis, Properties of Polymers, 4th Edition, Amsterdam (2009)
2. D.M. Koenhen and C.A. Smolders, J. of Applied Poly. Sci., Vol. 19, PP. 1163-1179 (1975)
3. S. Sugden, The Parachor and Valency, Routledge, London, 1930.
4. Robert C. Reid and Thomas K. Sherwood, The Properties of Gases and Liquids, New York 1958
5. Souheng Wu, Polymer Interface and Adhesion, Marcel Dekker, New York, 1982
6. B.B. Sauer and G.T. Dee, J. Colloid Interface Sci. 162 25 (1994)