Links:

Interfacial Properties
of Polymers

Wetting, spreading and adhesion phenomena are often described in terms of contact angles of liquids on a given surface. The figure below shows a solid surface (S) in contact with a droplet of liquid (L); we can distinguish between three different cases; if the liquid L fully wets the solid it tends to spread right over the surface. Thus, the contact angle θ is zero. In the second case, the liquid does not spread over the surface but does wet it. The contact angle is between 0 and 90° (π/2). The third case, describes a liquid that does not wet the surface, i.e. it shrink away from it. For this situation, the contact angle is greater than 90° (> π/2).

 

Contact Angle of Liquids at Solid Interfaces

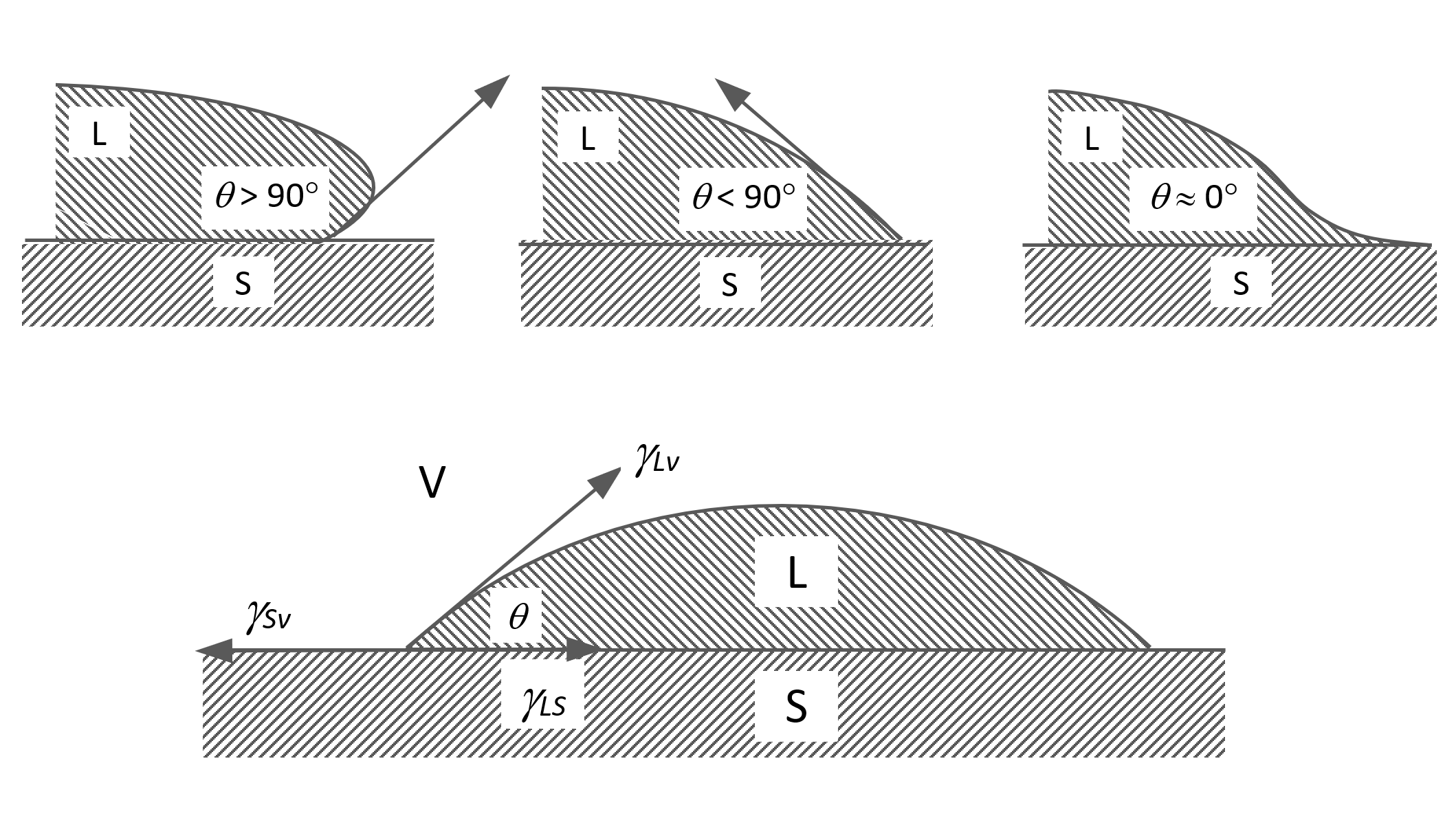
In the case of water, a surface is considered hydrophilic (or water-loving) when the static water contact angle is less than 90° and hydrophobic (or water-fearing) when the water contact angle is greater than 90°. Some materials strongly repell or attract water. These two extreme cases are known as ultrahydrophobicity  and ultrahydrophilicity.⁶ The definition of these terms is less precise. Ultrahydrophic (textured) surfaces are typically defined as materials on which water forms static contact angles of greater than about 150°⁷ whereas on ultrahydrophilic surfaces, droplets form a contact of less than about 20°. Hydrophobicity is often associated with oleophilicity (or oil-loving), which is the affinity of a surface for (hydrocarbon) oils which are non-polar organic compounds, whereas oleophobicity (or oil-fearing) describes the opposit phenomenom. A material is usually considered oleophobic when the critical surface tension decreases below 20 dynes/cm. These materials resist wetting by hydrocarbon solvents.

The contanct angle of liquids depends on the chemical nature of the material; in general, surfaces become more hydrophilic in the series: non-polar < polar but not hydrogen-bonding < polar and hydrogen-bonding < ionic. The surface roughness and surface texture as well as the number and type of sites at the interphase also have a significant effect on surface wetting.

 

Young's Equation and Spreading Coefficient

Equilibrium contact angles of liquids on solids are often described with the Young’s equation:

γ_sv = γ_sl + γ_lv cos θ

or

γ_lv cos θ = (γ_s - γ_sl) - (γ_s - γ_sv) =  (γ_s - γ_sl) - π_eq ≈ γ_s - γ_sl

where γ_sl, γ_lv and γ_sv are the surface tension at the solid-liquid, liquid-vapor and solid-vapor surface, respectively. The quantity γ_lv cos θ is called the adhesion or interfacial tension. Complete wetting occurs when cos θ = 1 or θ = 0. For this situation, the so-called spreading coefficient S, defined as

S = γ_sv - γ_lv - γ_sl,

is zero. Thus, for S < 0 the droplet will assume a finite contact angle and for S > 0 it will spread. Obviously, wetting is favored by a low interfacial free energy, a high solid surface energy and a low liquid surface free energy or surface tension. Unfortunately, only λ_LV and θ can be directly measured. However, in order to predict adhesion phenomena, we also have to know the surface tension of a solid λ_s. This quantity can be determined from the so-called Zisman plot. Fox and Zisman (1952) found that a plot of cos θ versus λ_lv for a homologous series of liquids on a given solid surface yields a straight line. Zisman was the first to introduce the concept of critical surface tension of wetting λ_cr, which is defined as the value of λ_lv, at the intercept of the cos θ - λ_lv plot with the horizontal line cos θ = 1 (Zisman plot).

 

Determination of Critical Surface Tension
using the Zisman and Fox Method

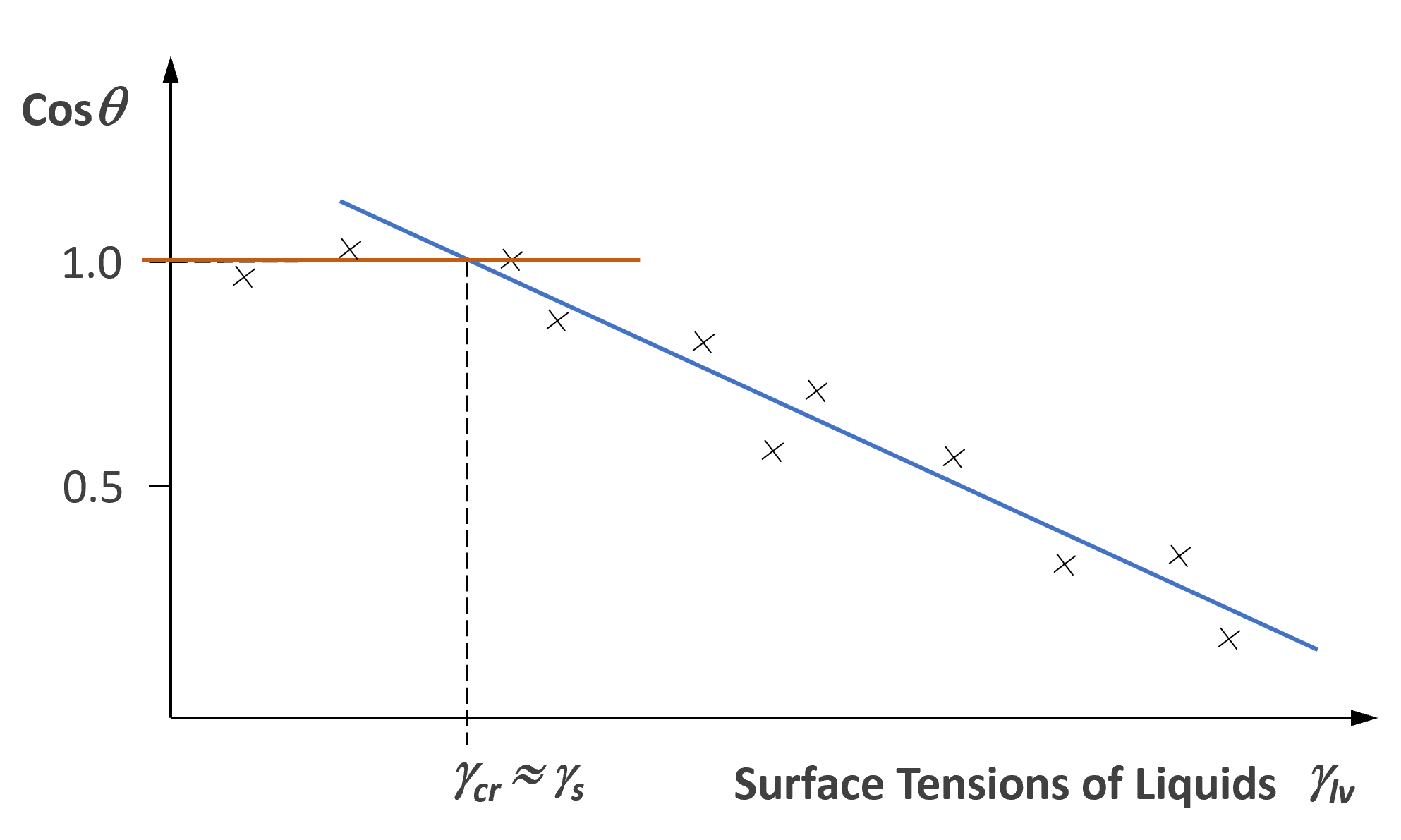
A liquid having a surface energy, λ_lv, less than the critical tension, λ_cr, will spread on the surface. Usually, λ_cr is very close to λ_s.

 γ_s ≈ γ_cr

The surface tension can also be calculated from the Girifalco and Good equation (1957):

 γ_sl =γ_sv + γ_lv - 2·Φ·(γ_svγ_lv)^1/2

where

Φ = 4(V_m,s·V_m,l)^1/3 / (V_m,s^1/3 + V_m,l^1/3)²

and V_m,l and V_m,l are the molar volumes of the liquid and the solid. In many cases, Φ is of the order of unity, which is the case for aliphatic compounds where only dispersion forces are present:

 γ_sl ≈ γ_sv + γ_lv - 2·(γ_svγ_lv)^1/2

Combining this equation with Young’s equation, gives

 γ_s ≈ γ_lv (1 + cos θ)² / 4Φ² ≈ γ_lv (1 + cos θ)² / 4

Another equation was suggested by Owens and Wendt (1969):

 γ_sl ≈ γ_sv + γ_lv - 2·[(γ_sv^dγ_lv^d)^1/2 + (γ_sv^pγ_lv^p)^1/2

In this equation, γ_sv^d is the dispersion force component and and γ_sv^p the polar force component of the surface free energy, i.e. γ_sv = γ_sv^d + γ_sv^p.

References & Notes

1. H.W. Fox and W.A. Zisman, J. Colloid Sci. 5, 514-531 (1950); 7, 109-121 and 428-442 (1952)
2. L.A. Girifalco and R.J. Good et al., J. Phys. Chem. 61, 904 (1957)
3. D.K. Owens and R.C. Wendt, J. Appl. Polym. Sci. 13, 1741 (1969)
4. A.B.D. Cassie, Discuss. Faraday Soc., 3, 11 (1948)
5. True and accurate surface tensions of polymers are excedingly difficult to obtain. A clean and smooth plastic surface is required which is difficult to maintain, because even a low energy surface will pick up contaminations from the environment during the manufacturing process and storage. If such contaminations are present, even only as a monolayer, it can act as a weak boundary layer and seriously affect the interfacial tension with other phases.
6. The two extreme cases are also referred to as superhydrophilicity and superhydrophobicity. The latter is also known as the lotus effect.
7. The theoretical maximum static contact angle for water on any smooth surface is 120°. However, when a hydrophobic surface is microtextured or micro-patterned, it can reach apparent contact angles of greater than 120°. This phenomenon is often described by Cassie's law:
   
         cos θ_c = ∑_i f_i cos θ_i = f₁ cos θ₁ - (1 - f₁) θ₂ = f1 (cos θ₁ +1) - 1
   
   where f₁ is the area fraction of the hydrophobic material in contact with water, θ₁ is the contact angle of water on the smooth surface, and θ₂ = cos(π) = -1 is the contact angle of water against air, which is assumed to be about 180°. Thus, the water-repelling quality of the lotus leave is due to its micro surface roughness (microscale bumps) and not to other causes, such as the presence of a coating with exceptional low surface tension.

Revised July 11, 2020