Polymers Modeled as Self-Avoiding Walks on Lattices
A polymer in an athermal solvent can be modeled as a self-avoiding walk (SAW) on a lattice. This model is very popular and has been used to describe the dynamic behavior of idealized polymer chains in solution both analytically and numerically. Because of its great importance in polymer science, the SAW problem has been studied by scientist and mathmathicians for more than half a century. So far, it has defied exact analytical solution even for relative short walks.
A self-avoiding walk (abbreviated as SAW) of length N on a lattice is defined by a sequence of vertices, ω0, ω1, ω2... ωn where ωi ≠ ωj if i ≠ j and where each vertex is the nearest neighbors of its predecessor. In other words, a SAW on a lattice is a random path which visits a lattice site not more than once. For example, a random walk on a square lattice with the the step increment |ωi - ωi+1| = 1 and length N = 4 might occupy following positions on the lattice
ω = {(0, 0), (1,0), (1,1), (1, 2), (2, 2)}
where we chose ω0 = (0,0) as the starting point of the walk.
Self-Avoiding Walk on Square Lattice
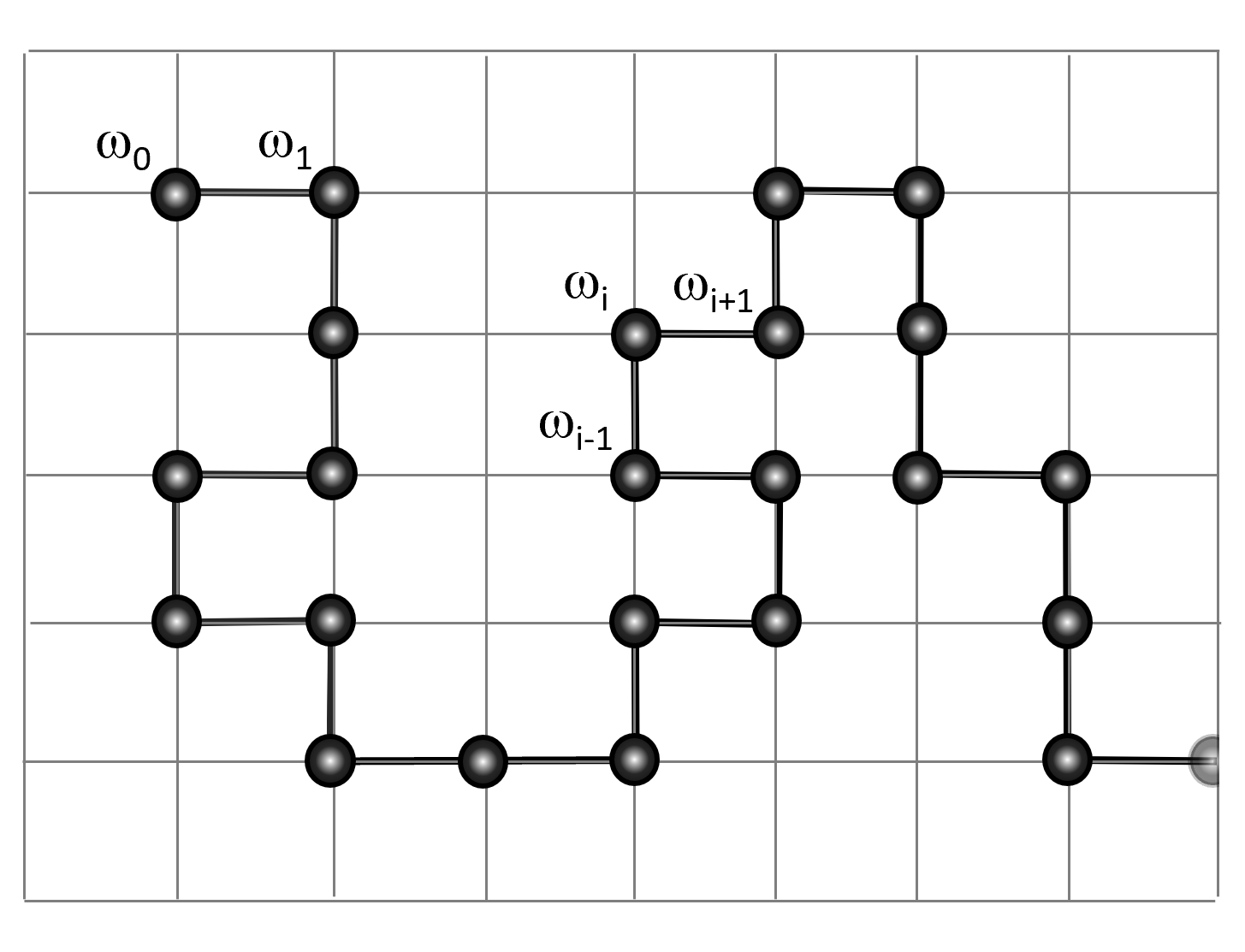
When analyzing self-avoiding walks, two basic questions arise: how many N-step self-avoiding walks exist (cN) and what is their (mean) dimension or size? The latter is often described as its square displacement Re2 (also known as its square end-to-end distance) or as its radius of gyration Rg2. For a SAW occupying the vertices ω = {ω0, ω1, ω2... ωN}, these two quantities can be calculated from
![]()
![]()
where |ωi| is the Euclidean distance. Of even greater importance are their mean (squared) values with respect to the uniform measure; for example, for walks of length N their mean values are given by
![]()
![]()
where cN is the total number of self-avoiding walks of length N. Although no method is available to calculate cN, 〈Re2⟩N, and ⟨Rg2⟩N for very long walks (N → ∞), it is believed that all three quantities have the asymptotic behavior:1-3
![]()
where A, B and C are referred to as the amplitudes and μ the connective constant 4. All four parameters depend on the type and dimension of the lattice whereas the critical exponents ν and γ (also called entropic exponent) are positive constants which depend only on the space dimensionality d but not on the particular lattice chosen. In fact, the same scaling relations hold for walks in the continuum which explains why lattice models of polymers correctly predict the asymptotic scaling behavior of polymers.
The values of the critical exponents have been calculated by several authors. For d = 2 the exact results are3
ν = 3/4, γ = 43/32
whereas for d = 3 only estimates are available:3
ν ≈ 3/5, γ ≈ 7/6
As Flory has shown, the exponent ν can be estimated from ν = 3 / (d + 2).6
The connective constant μ is defined by the limit4
![]()
and is believed to exist and to be finite. Some of the best numerical estimates of μ for the square and simple cubic lattice are,3,5,10
μsquare ≈ 2.63815853...
μcubic ≈ 4.68404...
However, the exact value of the connective constant is unknown for lattice walks in three and higher dimensions,
d > 2.
The amplitudes of the SAW have been determined for several lattices with
high to moderate accuracy. For the square and simple cubic lattice
they read3,7
ASQL ≈ 1.1771, BSQL ≈ 0.771,
ASCL ≈ 1.205, BSCL ≈ 1.2167, CSCL ≈ 0.1946
With the exception of very short walks, the deviations between the exact numbers of self-avoiding walks and those calculated with the approximation cN ≈ A μN Nγ-1 are typically less than 1% and often less than 0.3%.8 The number of self-avoiding walks cN can also be calculated (or estimated) using the inclusion-exclusion principle from combinatorics. This method avoids the time-comsuming enumeration of SAWs.
Interacting Lattice Chain
In the case of interacting lattice chains or lattice chains near a barrier, not all walks are equally likely. For example, to model the collapse of a polymer chain in a bad solvent, attractive interactions between (non-consecutive) nearest-neighbor lattice "monomers" have to be taken into account, that is two vertices adjacent on the lattice but not connected by an edge have to weighted by
![]()
where ε is the interaction energy between nearest-neighbor vertices, kB is the Boltzmann constant and T is the absolute temperature. The conformational partition function is then
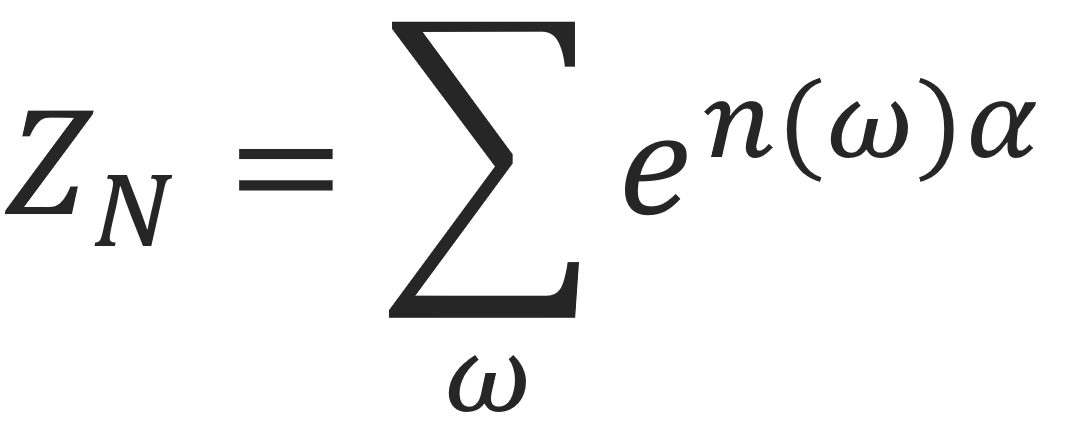
where the sum is over all SAWs ω of N steps, and n(ω) is the number of pairs of nearest-neighbor contacts which occur in ω. The average conformational energy of the lattice chain is obtained from
![]()
and the conformational entropy is obtained from
![]()
A similar approach can be used to derive average conformations of local portions of the lattice chain, for example a portion that is adsorbed onto a surface.
References & Notes
C. Domb and M.F. Sykes, Phil. Mag., 2, 733 (1957)
M. E. Fisher, M. F. Sykes, Phys. Rev., 114, 45 (1959)
K.Y. Lin and M. Chen, J. Phys. A: Math. Gen., 35, 1501-1508 (2002)
μ is sometimes called the growth constant of the self-avoiding walk and κ = log μ the connective constant.
D. MacDonald, S. Joseph, D. L. Hunter, L. L. Moseley, N. Jan and A. J. Guttmann, J. Phys. A: Math. Gen., 33, 5973 (2000)
Paul L. Flory, Principles of Polymer Chemistry, Ithaca, New york, 1953
K.Y. Lin and Y.C. Hsaio, Chinese J. of Phys., 31, 6-I (1993)
Schram et al. developed a new methodology of enumeration, which allowed to enumerate self-avoiding walks on the simple cubic lattice up to a length of 36 steps using 50,000 hours of computing time. They fitted their data with the function9
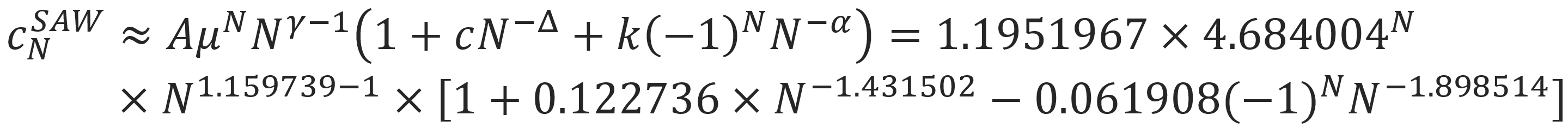
For large numbers, the deviations between cN and the fitted numbers show up in only the seventh or eight significant digit whereas for short walks (N < 12) the deviation is much larger but less than 1%.
R.D. Schram, G.T. Barkema, and R.H. Bisseling, J. Stat. Mech.: Theory and Experiment,
Vol. 2011, P06019 (2011)-
The exact value of the connective constant μ for any three dimensional lattice (d ≥ 2) is unknown.11
-
Gordon Slade, Proc. R. Soc. A 475: 20180549 (2019)