Phase Behavior of
Ternary Polymer Mixtures
Part 3
Most products made of polymers are blends of more than two components and, in many cases,
of more than one polymer. The thermodynamics of these mixtures can be described with
the compressible regular solution free energy model of Ruzette and Mayes (2001)1,2.
This model makes only use of pure component properties which are assumed to be
concentration and temperature dependent, that is, the model avoids the direct
calculation of the temperature and concentration dependency of the Flory-Huggins interaction
parameter.
Once all pure component properties have been
calculated, the ternary phase curves for
weakly interacting polymer systems can be easily calculated. The spinodal
points which define the boundary between the stable and
metastable regions are usually sufficient to qualitatively
describe the phase behavior of ternary systems. Following
Scott3,4, the stability criterion for spinodal points of ternary
systems are found by solving following equation:
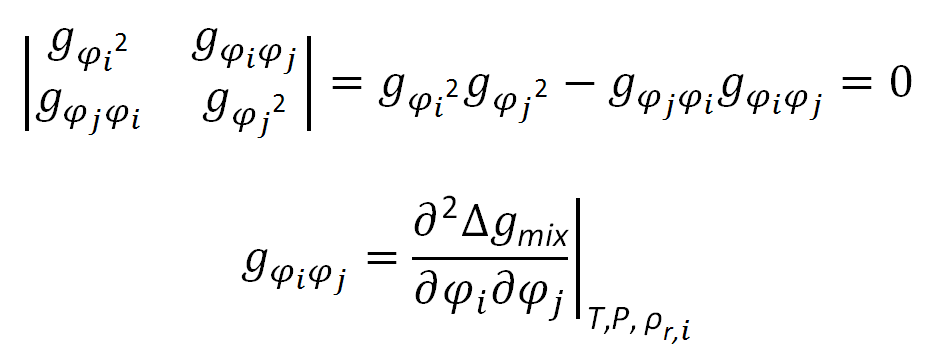
Scott's spinodal condition has the following solutions:
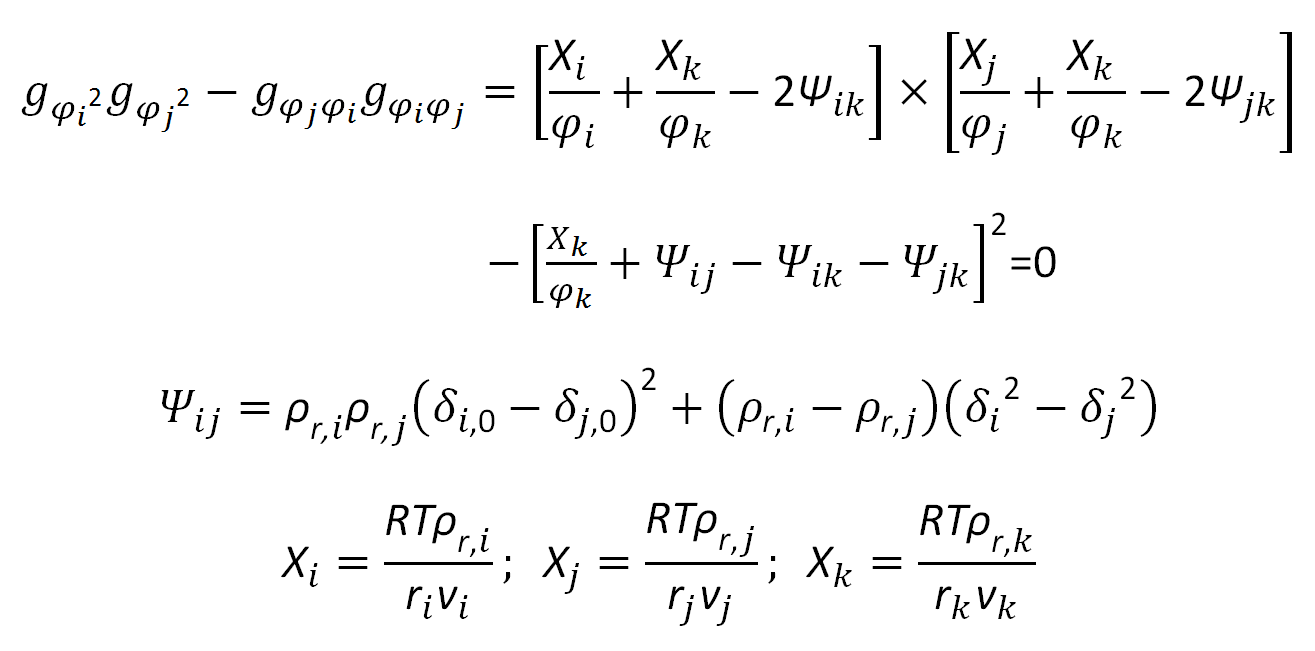
where ρr,i = ρi / ρhc,i = vi / vhc,i is the reduced density5, δ0,i2 = ρr,i, δi2 is the corresponding hardcore cohesive energy density, and φ1 and φ2 are the volume fractions of the two components,
φi = Ni ri vi / Σ(Nj rj vj )
The compressible regular solution model presented here is only applicable to weakly interacting systems. As Gonzales and Ruzette have shown2, the agreement with the experimental data for those sytems is quite good, despite the many simplifying assumptions of the model.
References & Notes
Anne-Valerie G. Ruzette and Anne M. Mayes, Macromolecules 34, 1894-1907 (2001)
Juan A. Gonzalez-Leon and Anne M. Mayes, Macromolecules 36, 2508-2515 (2003)
R. L. Scott, J. Chem. Phys. 17, 268 (1949)
R. Scott, J. Polym. Sci., Vol. 9 (5), pp. 423-432 (1952)
The hard core volume is the volume of a repeat unit at zero Kelvin and zero pressure. Most investigators assume that vhc is equal to the closed packed volume of the molecules at zero Kelvin.
July 30, 2020