Rotational Isomeric State Model
Part 2: Interdependent bond Rotations

The rotational isomeric state approximation (RIS) for polymers was first introduced by Flory and Volkenstein. To simplify the calculation, they assumed that each molecule can be treated as if it exists only in discrete torsional states corresponding to the potential energy minima of the rotational configuations (see below). Thus, any variations around the local minima of the rotational state is ignored. For example, a polyethylene chain with a symmetric three-fold torsion potential has the rotational isomeric states: trans (φ = +180°), the gauche⁺ (φ = +60°) and gauche^- (φ = -60°), termed t, g⁺ and g^-.

 

rotational isomeric states in polyethylene

 

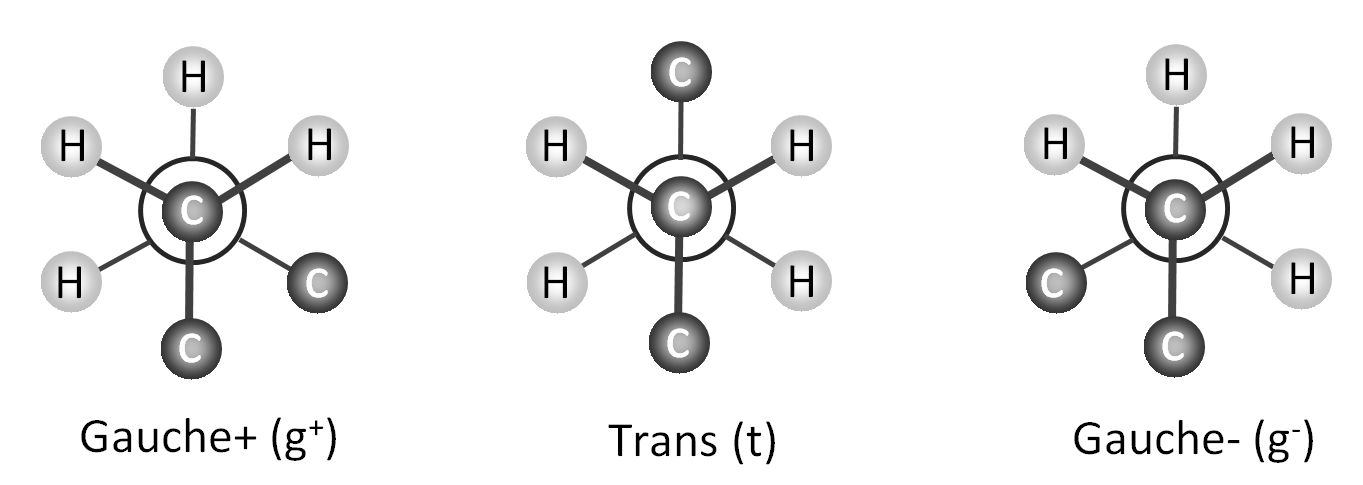
Flory and Volkenstein assumed that the conformational energy is not only affected by the interaction of neighboring groups, i.e. by groups that are separated by three bonds (t, g⁺ and g^-), but that groups separated by four bonds are also affecting the conformational energy because these can be in close proximity which leads to strong steric interaction. This interaction is known as the pentane effect. It causes the energies of g⁺g^- or g^-g⁺ arrangements to be much higher than those of g⁺g⁺ or g^-g^-.

Assuming bond i has the torsion angle φ_i and the preceding bond i-1 the angle φ_i-1, the conditional probability or statistical weight P(φ_i|φ_i-1) reads

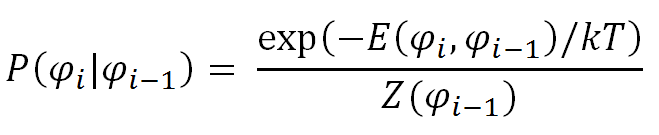
where Z is a normalizing factor which is the sum of the Boltzman energy for all angles φ_i and fixed angle φ_i-1:

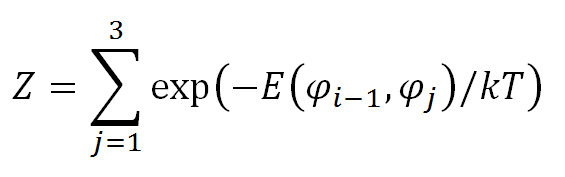
By combining each of the three states of the first unit with those of the second, we get nine rotational isomers which we can group into three pairs: {tt, g⁺t, g^-t}, {tg⁺, g^-g⁺, g⁺g⁺}; and {tg^-, g^-g^-, g⁺g^-}. The conditional probabilities of these states can be collected in a weight matrix:

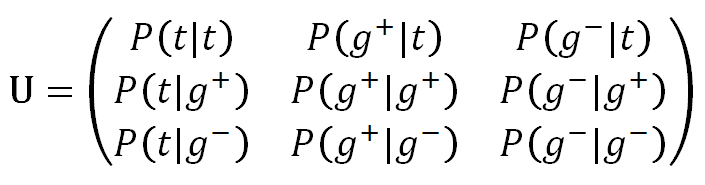
The lowest of these rotational energy states is tt which we arbitrarily assign to the ground state: E(tt) = 0. The tg⁺ and tg^- bond pairs will each be higher in energy than the tt state and their excess energy, E_g, is about the same. Assuming the preceding bond is in the trans state, the partition function Z for the bond pairs reads

Then the three states of the first row of the weight matrix have the conditional probabilities:

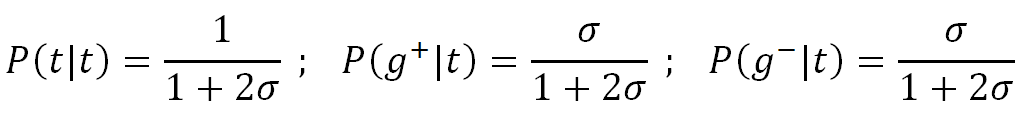
If, on the other hand, the preceding bond is in the gauche+ state (second row) the partition function Z reads

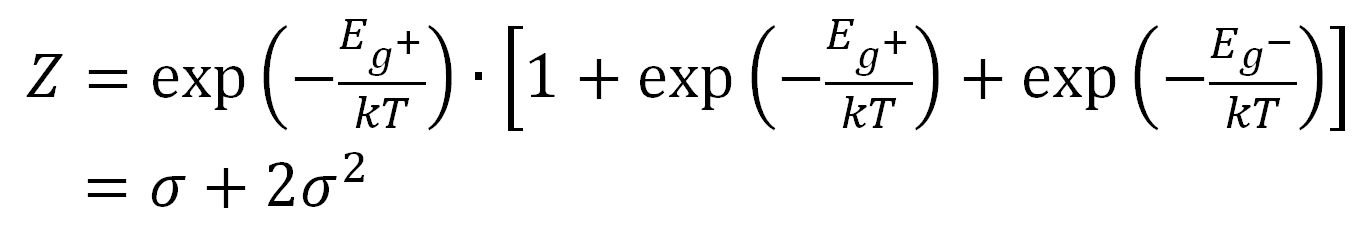
Then the three conditional probabilities are

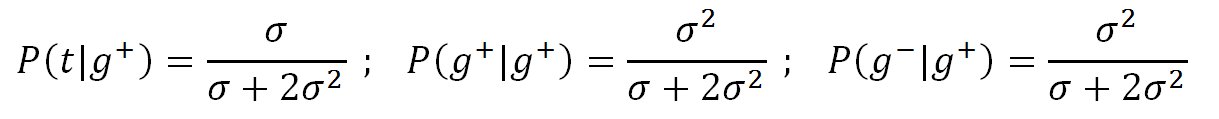
The same conditional properties appliy if the first bond is in the gauche- state.
Above we ignored the short-range interaction that occurs when two consecutive bonds are in the g⁺g^- or g^-g⁺ state. This so called pentane effect increases the energy by E_p or E(g⁺g^-) = 2E_g + E_p whereas E(g⁺g⁺) = 2E_g. With ω = exp(-E_p/kT) the conditional probabilities of the second and third row read

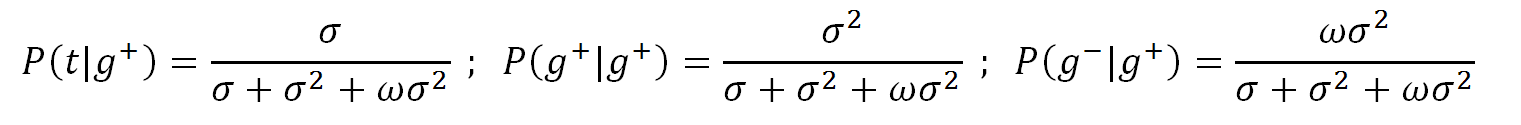
Then the generalized statistical weight matrix takes the form

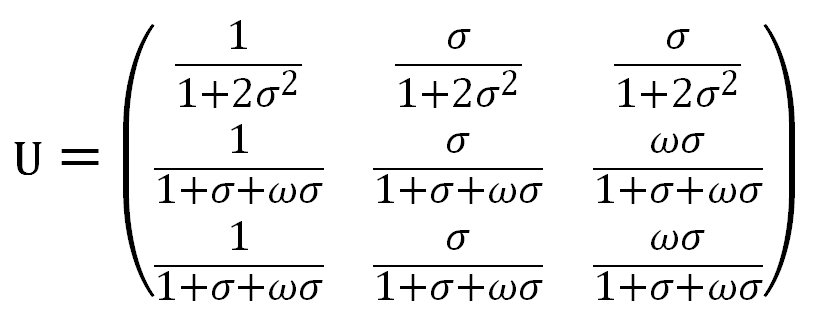
When normalizing each row to the first element in that row, the weighting matrix of the relative probabilities can be written as

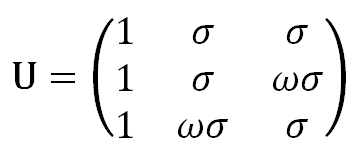
As has been shown by Flory and others, the partition function of a polyethylene chain can be directly calculated with this matrix:

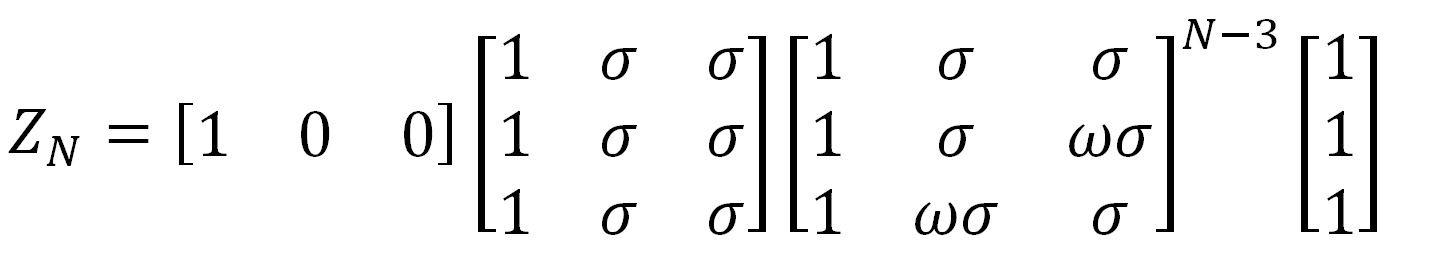
Similar statisitical matrices can be derived for other polymer chains. However, the interaction is more complex due to the larger number of different atoms involved. For example, polyoxyethylene has three distinct statistical weight matrices.

An obvious drawback of the RIS-model is that it does not account for long-range interaction, i.e. molecules that are separated by more than four bonds. However, it still provides a microscopic understanding for all situations with ideal chain behavior.

References

1. P.J. Flory, Statistical Mechanics of Chain Molecules, Wiley, New York (1969)
2. M.V. Volkenstein, Molecular Biophysics, Academic Press, New York 1977