Poisson Ratio of Polymeric Materials
When a material is stretched by a tensile force it usually undergoes a lateral contraction which is known as the Poisson effect.1 The ratio of the lateral contraction (or compression) and longitudinal extenion is called the Poisson's ratio.
ν = -εlateral / εlongitudinal
where the minus sign accounts for the negative strain. At low strain (< 1 %), the deformation of most polymeric materials is elastic, that is, the deformation is homogenous and after removal of the deforming load the material returns to its original size and shape. If an isotropic material is only subjected to a tensile force in the x direction, the strain within the elastic limit obeys Hooke's law:
εx = σx / E
where E is the Young's modulus (also called elastic modulus or tensile modulus). Then the strain in the other directions is simply
εy = εz = -ν εx
If, on the other hand, a material is subjected to both longitudinal stress (σx) and lateral stress (σy), the effect of both stresses can be superimposed. Then the strain in the x and y direction is given by
εx = σx / E - ν σy / E = (σx - ν σy) / E
εy = σy / E - ν σx / E = (σy - ν σx) / E
The material is in a state of plane stress if the stress in the z direction can be neglected (σz = 0). This situation is often encountered in thin sheet samples. However, the strain in z direction can not be neglected. In general, a sheet sample will undergo a strain in the z direction equal to the Poisson strain contributions of the stresses in the x and y direction:
εz = - ν (σx + σy) / E
Poisson Effect
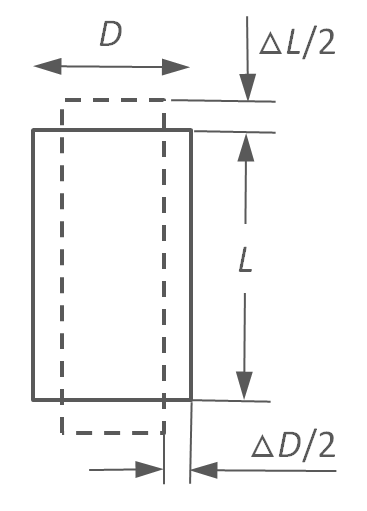
The total strain in each direction can be obtained by superposition of the effects of all nominal stresses:
εxx = [σxx - ν (σyy + σzz)] / E
εyy = [σyy - ν (σxx + σzz)] / E
εzz = [σzz - ν (σxx + σyy)] / E
These equations are known as the generalized Hooke's law for normal stresses in three dimensions. The sum of the strains εxx + εyy + εzz is called the volumetric strain or dilatation. The volumetric strain of rubbery materials it is often close to zero. Thus rubbers are oftent assumed to be incompressible.3
For isotropic materials, the Poisson's ratio ν must satisfy –1 ≤ ν ≤ ½. In the case of a weakly compressible material such as liquids and rubbers, a stress primarily results in shape change. In this case, the Poisson's ratio approaches the value ν = 0.5. For most solids such as metals, engineering plastics and ceramics, ν is in the range4
0.25 < ν < 0.35.
The Poisson’s ratio is intimately related to the packing density, i.e. to the way the atoms/molecules or repeat units are packed. For most polymers, it decreases with increasing packing density. Thus, crystalline polymers have a smaller Poisson's ratio than amorphous polymers.
The Poisson’s ratio of polymeric materials is often assumed as constant. However, it is a viscoelastic property and hence depends on many factors such as temperature, time, strain and strain rate. The Poisson’s ratio of polymeric materials generally increases with time, strain and temperature, and decreases with strain rate.
References and Notes
This fundamental material property was first introduced by Siméon Denis Poisson (1787–1840)2 who explored and solved many fundamental problems of mathematical physics.
S.D. Poisson, Traite de Mecanique, Paris 1811
-
This assumption is only an approximation because for an incompressible material (ν = 0.5) the bulk modulus will go to infinity which is not possible.
For auxetic materials the Poisson's ratio is negative. These materials expand in transverse direction when stretched and contract in transverse direction under compression load. Auxeticity is a common phenomenon in a number of crystalline materials and network polymers like auxetic polyurethane foam where ν can be both positive and negative, depending on orientation.
M.D Lechner, K. Gehrke, E.H. Nordmeier, Makromolekulare Chemie, 1993
G.N. Greaves, A.L. Greer, R.S. Lakes and T. Rouxel, Nature Mater. 10, 823-837 (2011)
N.W. Tschoegel, W.G. Knauss & I. Emri, Mechanics of Time-Dependent Materials 6: 3–51 (2002)