Polymers at Interfaces
Part1: Structure of Adsorbed Polymer Layer

In the last 25 years numerous analytical self-consistent mean-field models were proposed to predict the structure of adsorbed polymers at a solid interfaces. Some of the most elegant analytical mean-field models that go beyond the standard ground state dominance approximation were developed by Semenov, Bonet-Avalos, Johner, Fleer, Leermakers and Joanny.^1-7 Their models describe the random conformations and the equilibrium volume fraction profile of homopolymers reversibly adsorbed from solutions onto homogenous surfaces.

The structure of adsorbed polymer chains can be described in the terms of trains, loops and tails (see figure below). Trains consists of adjacent segments all adsorbed at the surface, whereas loops are non-adsorbed parts in-between two trains. There are also one or two tails at the end of the adsorbed polymer chain, i.e. open loops. The way in which the polymer segments are distributed over the trains, loops, and tails largely determines the physical properties of the adsorbed polymer layer.

  

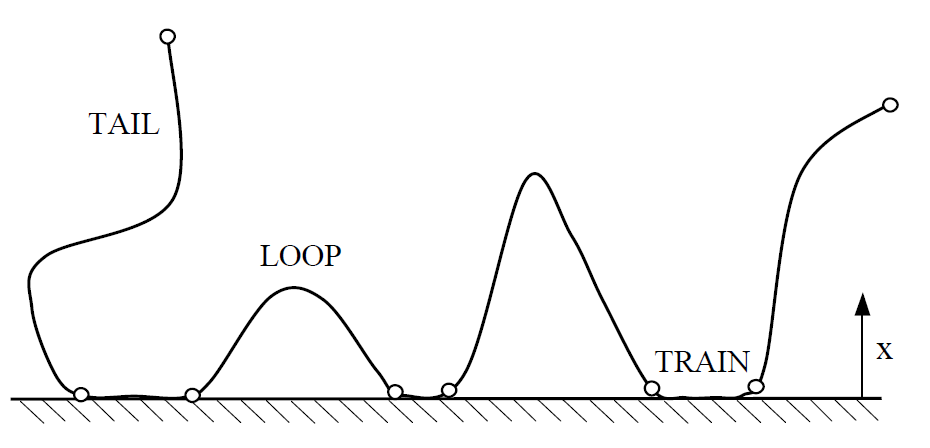
For polymers near an interface, the adsorbed polymer layer, i.e. its concentration profile, can be divided in three distinct regions:^4,8

• Proximal (x ≈ 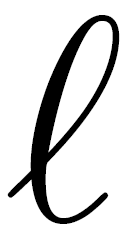< D): This region is closest to the surface within a distance D, comparable to the size of a segment. In this region, short-range forces between the segments and the surface are important which are often assumed to be of short range, i.e. the adsorption force is only felt by segments in direct contact with the surface.

• Central (D < x < ξ): In this intermediate range, the segment volume fraction φ_P(x) is high and the segment potential u(x) dominates over the surface potential u(x=0). Furthermore, the contribution of loops (φ_P^l) dominates over that of tails (φ_P^t) and universal scaling relations apply.

• Distal (x > ξ): In this outer region, the contribution of tails (φ_P^t) dominates over that of  loops (φ_P^l) and the concentration drops exponentially toward the bulk value, φ_P(x) ≈ φ_P^∞ [1 + e^-2x/ξ ]

The critical crossover distance ξ between the central and distal regions depends on the polymer concentration; in a semi-dilute solution, the cut-off length ξ is approximately equal to the bulk correlation length ξ_b and in a very dilute solution it is equal to the radius of gyration R_g ∼ N^ν of the polymer chain.^4,8

The total polymer volume fraction in the adsorbed layer has contributions of trains (tr), loops (l), and tails (t) of adsorbed chains and contributions of free chains (fr):¹⁰

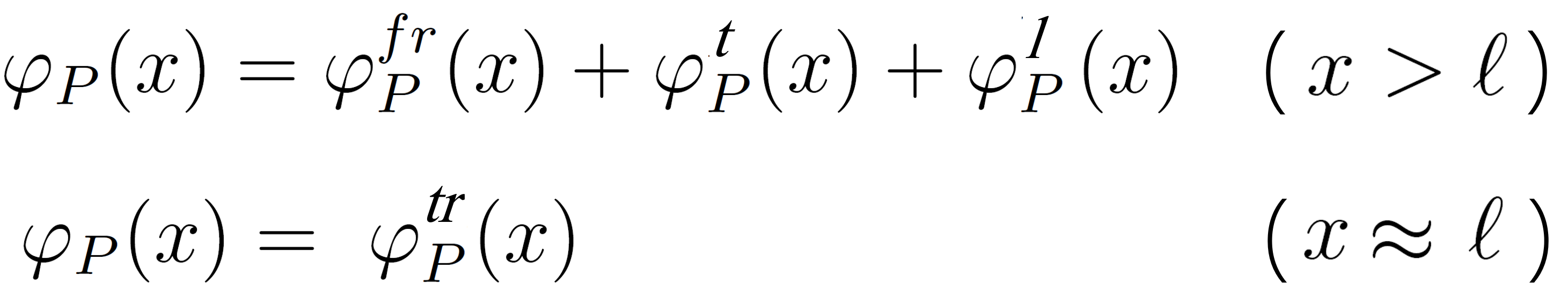
The polymer volume fraction of the segments, φ_P(x,s), can be calculated from the end segment probability G(x,s) which is the probability that a chain of s segments has one of its end point in the plane x parallel to the interface.¹¹ Using the the so-called composition law⁹ and the boundary condition for the end points, φ_P(∞, s) = φ_P^b / N, the end segment volume fraction φ_P(x,s) can be written as:⁹

The total monomer concentration at point x can be found by integration over s: 

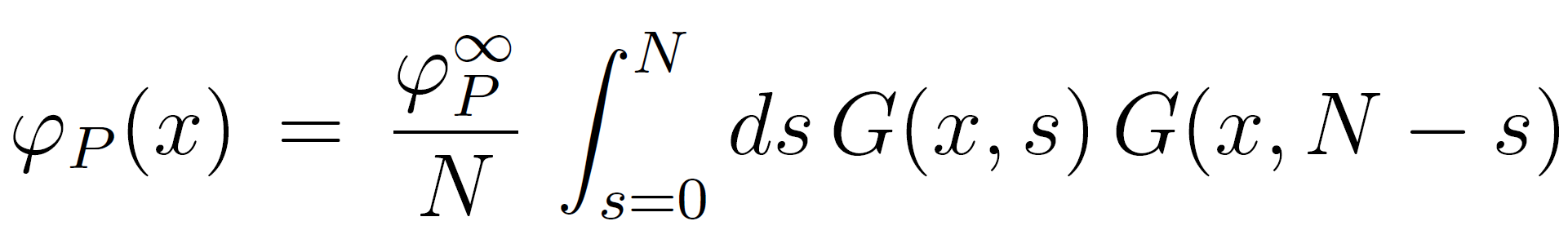
Similarly, we can obtain expressions for the contributions of ends, loops, trains, and free chains:⁴

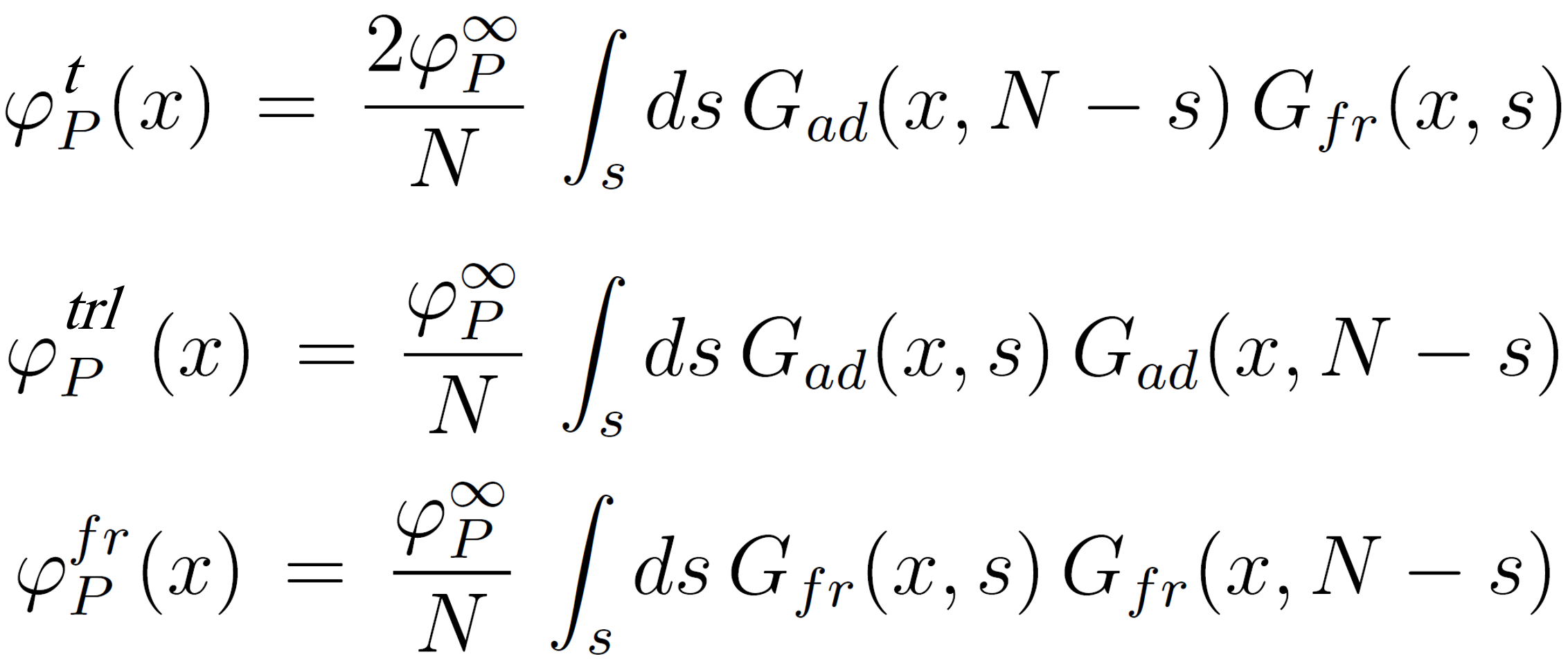
where G(x,N) has been separated into a contribution G_ad(x,N) due to adsorbed chains and a contribution G_fr(x,N) due to free chains. 

Another important property is the (adsorbed) amount in equivalent numbers of monolayers:

θ_S can also be obtained as θ_tr^tr + θ_S^l + θ_E^t. These three quantities can be calculated from the train, loop, and tail volume fractions:

The structure and volume fraction profiles of adsorbed and free polymers in the surface layer can be calculated with the mean-field theory with two order parameters.^4,6 Then two Schroedinger-like equations for the partition function of adsorbed and free chains have to be solved. As will be shown in part 2, this is a complicated problem. The calculation involves several approximations which are necessary to render the analytical problem tractable.

References and Notes

1. A. Johner, J.F. Joanny, M. Rubinstein, Europhys. Lett. 22, 591 (1993)

2. A.N. Semenov, J.F. Joanny, Europhys. Lett. 29, 279 (1995)

3. A.N. Semenov, J. Bonet-Avalos, A. Johner, J.F. Joanny, Macromolecules 29, 2179 (1996)

4. A. Johner, J. Bonet-Avalos, C.C. van der Linden, A.N. Semenov, J.F. Joanny, Macromolecules 29, 3629 (1996)

5. J. Bonet Avalos and A. Johner, Faraday Discuss. 98, 111-119 (1998)

6. G.J. Fleer, J. van Male, A. Johner, Macromolecules 32, 825 (1999) & 32, 845 (1999)

7. G.J. Fleer, F.A.M. Leermakers, Macromol. Symp. 126, 65 (1997)

8. P.G. de Gennes, Macromolecules 14, 1637-1644 (1981) & 15, 492-500 (1982)

9. G.J. Fleer, M.A. Cohen Stuart, J.M.H.M. Scheutjens, T. Cosgrove, B. Vincent; Polymers at Intefaces; Chapman & Hill, Cambridge (GB) 1993

10. It is assumed that the segment distribution is uniform in the y,z plane.

11. This quantity is also called the end-point distribution, the end segment distribution function or the end segment partition function.