Polymers Near Interfaces
Analytical Mean Field Theory

In the last 50 years several analytical self-consistent mean-field models were proposed to predict the behavior of polymers near interfaces. Most of these models describe either the behavior of isolated polymers near a (solid and flat) surface or the adsorption of polymers from polymer solutions onto homogenous surfaces.

Two of the oldest analytical mean-field models were developed by De Gennes and Edwards in the 1960s and 1970s.^1-4 They were the first to realize that the random conformations of a polymer chain resemble the path of a diffusing particle and that its segment distribution can be described by a diffusion-like equation. To do so, the time variable in the diffusion equation has to be replaced by the ranking number (s) in the polymer chain. For a purely random walk in one direction the diffusion equation reads

where G(s,x) is the end segment probability distribution that a chain of s segments and length reaches the point x. This quantity is also called the relative weight with respect to the homogenous solution.⁵

  

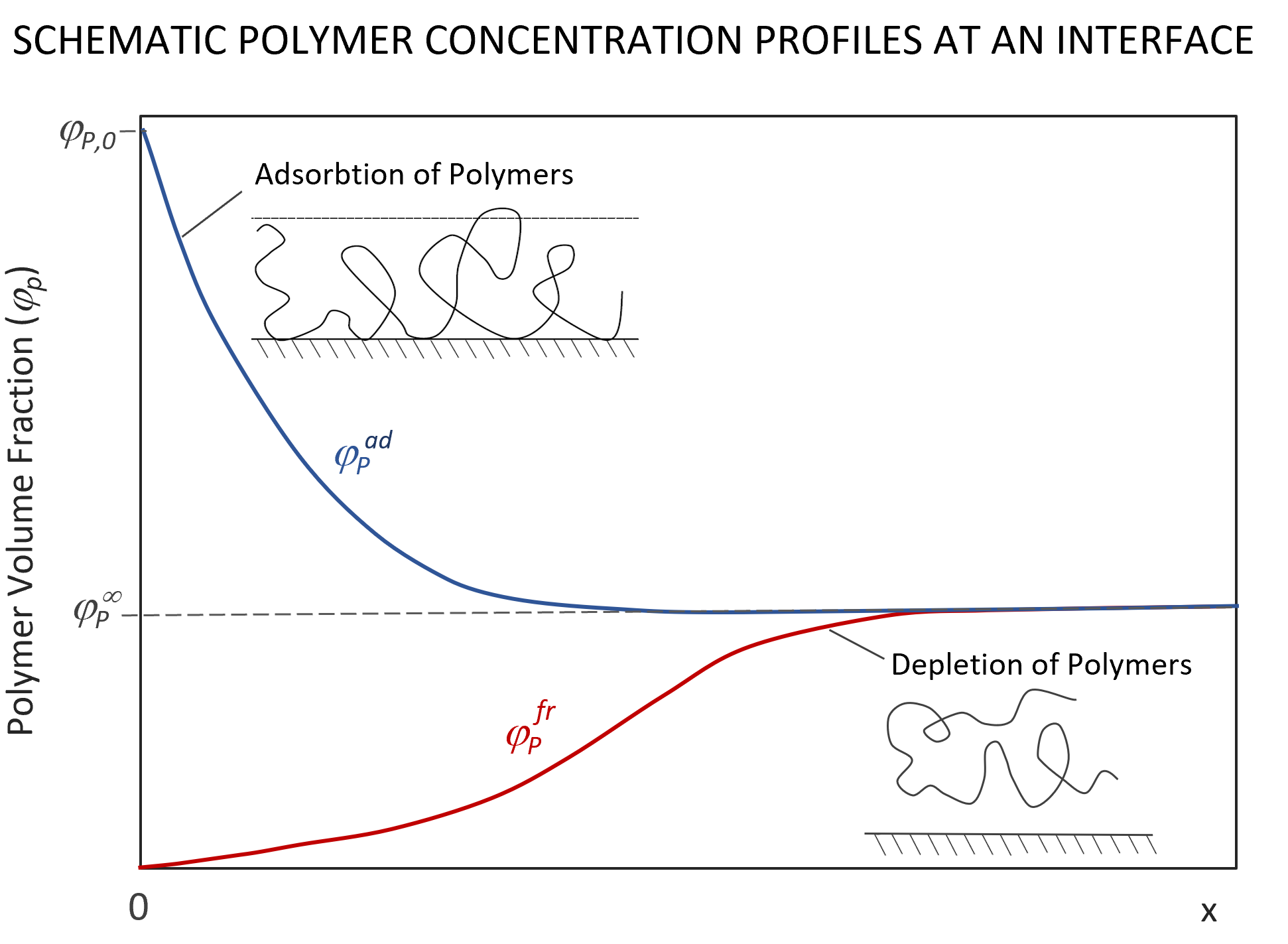
For polymers near an interface, the distribution of polymer segments, i.e. its concentration profile, will be affected by an attractive or a repulsive segment-interface potential u(0) = e^χs.⁶ As has been shown by Edwards, de Gennes and others, the segment distribution of polymers near an interface is governed by a Schroedinger-like equation:^4,5,7-9

where (²/6) ∂²/∂x² + u(x) / kT equals the Hamilton operator H and G(x, s) replaces the wave function ψ(x). The quantitiy u(x) is the segment potential with respect to the (homogenous) bulk solution. It depends on the chemical composition of the interface, the type of polymer and solvent, and the local segment concentration φ_P(x) making it a self-consistent potential. For x ≤ 0, u(x) = ∞ and G(x) = e^-u(x)/kT = 0, whereas for large x, u(x) ≈ 0 and G(x) ≈ 1.

The solutions of the above Schroedinger-like equation have the form

where g_k(x) are eigenfunctions and ε_k their eigenvalues which satisfy the eigenvalue equations H g_k(x) =  (²/6) ∇² g_k(x) + u(x) / kT g_k(x) =  ε_k g_k(x). For very dilute polymer solutions or for isolated polymer chains, the largest eigenvalue ε_k dominates in the expansion. For this case, the x- and s-dependencies can be separated:

This approximation is called the ground state dominance which satisfies following groud state equation:

Let us assume that we have already found a solution of the ground state equation. Then the polymer volume fraction of the segments, φ_P(x, s), can be calculated with the so-called composition law^5,11,12

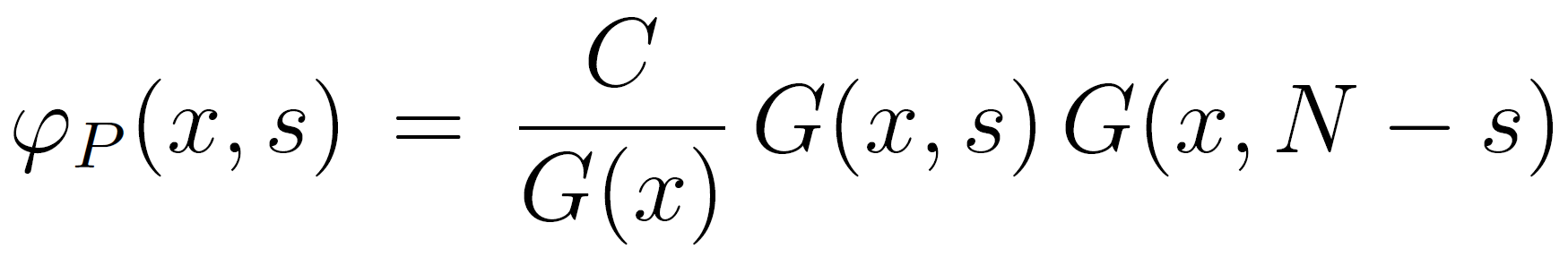
Substituting G(x,s) with the ground state solution, we obtain for the polymer volume fraction

where C is a normalization constant which can be determined from the boundary condition of the end points: φ_P(∞, s) = φ_P^b / N. Since G(x=∞; s) = 1 and u(x) = 0, the normalization constant is simply given by C = φ_P^∞ / N.^5,12

The total monomer concentration at point x can be found by integration over s:

For very low concentrations (isolated chains), u(x) ≈ 0 and φ_P^∞ exp(N ε₀) ≈ 1. Then the above expression for the segment concentration reduces to

The distribution of segments near the interface depends on the surface potential u(0). In the case of an attracting interface, segments will accumulate near the surface which will change the potential in its vicinity. Therefore, u(x) is a function of the segment volume fraction profile φ_P(x) which, in turn, is a function of the field, G(s,x), i.e. the field has to be self-consistent. To simplify the problem, the interface potential is often assumed to be of short range, i.e. only nearest neighbor interactions are taken into account. In other words, the adsorption energy is only felt by segments in contact with the surface. This self-consistent field can be described as an extended Flory-Huggins field:^5,12

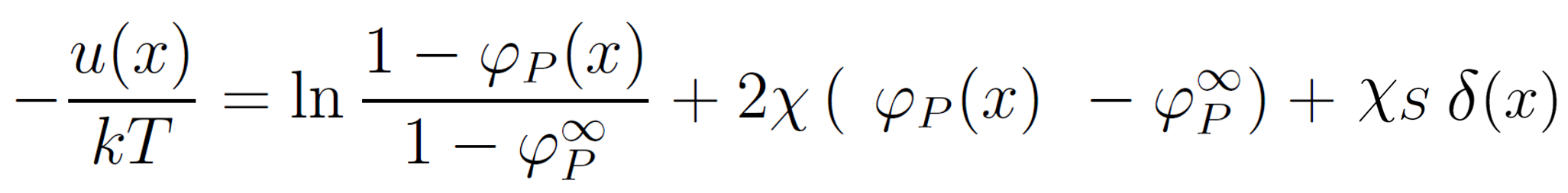
For very low polymer volume fractions in the bulk φ_P^∞ → 0, the expression above can be rewritten as^10,12,20

where χ is the Flory-Huggins parameter and χ_s = (u_1s - u_2s) / kT is a dimensionless adsorption (desorption) energy parameter first introduced by Silberberg.¹⁴ This parameter describes the change in potential energy Δu when a solvent molecule (1) is displaced by a segment (2) at the interface.¹⁵ If this parameter is positive, polymers adsorb from the solution whereas for negative values and even small positive values the polymers desorb and avoid the interface due to a loss of conformational entropy in the vicinity of the surface (negative adsorption or depletion). In other words, polymer chains only accumulate near an interface if the adsorption energy parameter exceeds a critcal value χ_s^crit = -ln(1 - λ) - λχ, where λ = 1/6.¹²

In a good solvent (χ ≤ 0) and for low polymer volume fractions (φ_p << 1), the above expression for u(x) can then be simplifies to

The ground-state approximation (GSA) for dilute polymer solutions (small φ_p) near an desorbing barrier can be written as

where φ_p ≈ |g₀|² and v is the excluded volume parameter.⁷ The boundary conditions are g₀(0) = 0 and lim_{x → ∞} g₀(x) = φ_p^∞1/2. The above GSA can be evaluated by partial integration, which gives

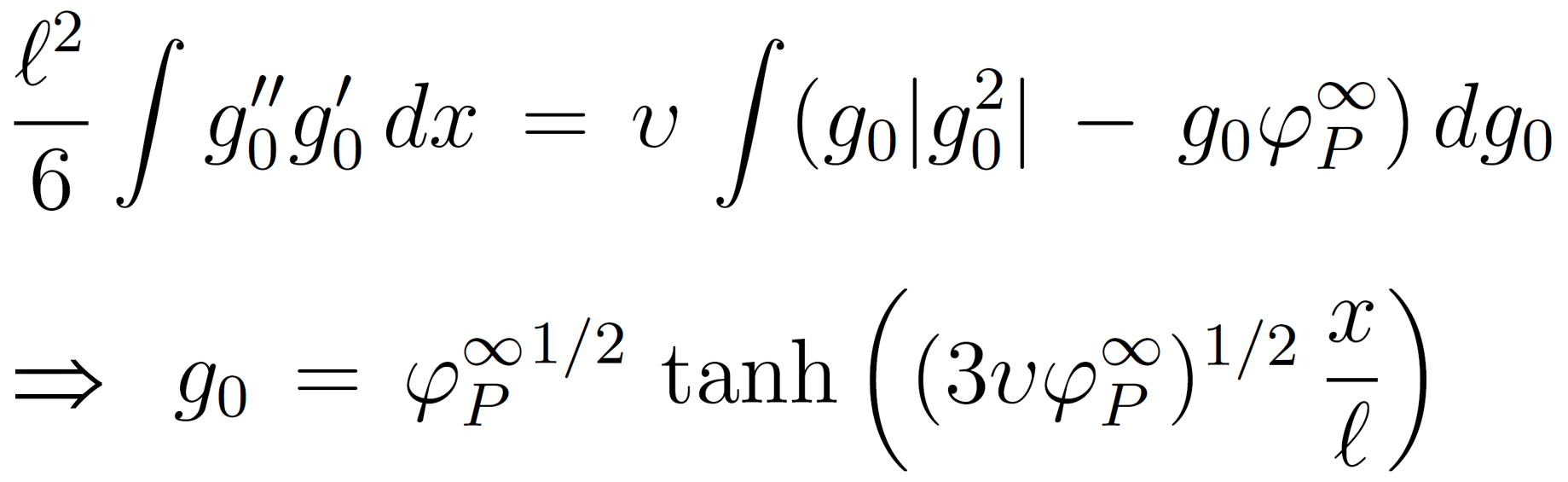
The segment concentration at point x can then be calculated as^5,10,17

where is the bulk correlation length.^10,16 This parameter depends on the concentration but not on the chain length, i.e. the number of segments.¹⁸

In the case of a weakly adsorbing surface, the boundary conditions read¹⁹

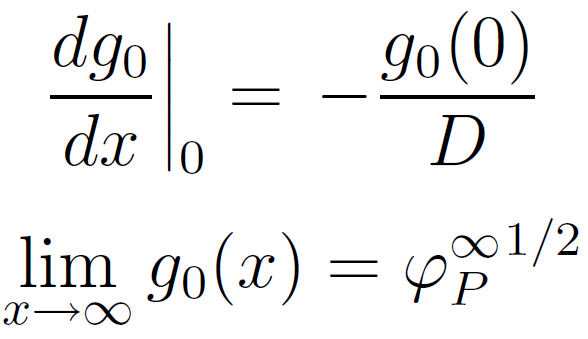
where D is the thickness of the proximal region (also called adsorption or extrapolation length) where short-range forces between monomers and the wall are important.¹⁹ Solving the differential equation with these conditions and g₀ ≥ 1 gives

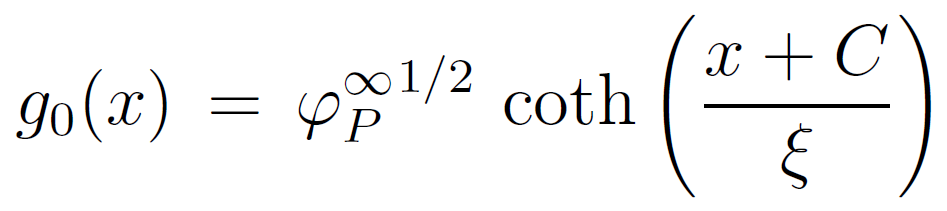
where C is an integration constant which has the value

As has been shown by Semenov, Johner, Fleer and others,^5,13,16 the ground-state approximation is only valid for very long chains (N → ∞) in very dilute solution and for isolated adsorbed chains in the vicinity of an interface. It also may be used to predict the volume fraction profile of interacting polymers near a non-adsorbing surface.

References and Notes

1. P.G. De Gennes, Rep. Prog. Phys., 32, 187 (1969)

2. P.G. De Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, New York, 1979

3. S.F. Edwards, Proc. Phys. Soc., 85, 613 (1965) & 88, 265 (1966)

4. S.F. Edwards, Proc. R. Soc. Ser. A, 343, 427 (1975)

5. G.J. Fleer, M.A. Cohen Stuart, J.M.H.M. Scheutjens, T. Cosgrove, B. Vincent; Polymers at Intefaces; Chapman & Hill, Cambridge (GB) 1993

6. It is assumed that the segment distribution is uniform in the y,z plane.

7. J.F. Joanny, L. Leibler u. P.G. de Gennes, J. Poly. Sci.: Poly. Phys. Ed. 17, 1073 (1979)

8. I.S. Jones, P. Richmond, J. Chem. Soc. Faraday II 73, 1062 (1977)

9. P.R. Gerber, M.A. Moore, Macromolecules 10, 476 (1977)

10. J. Bonet Avalos and A. Johner, Faraday Discuss. 98, 111-119 (1998)

11. H.J. Ploehn, W.B. Russel, C.K. Hall, Macromolecules 21, 1075 (1988)

12. G.J. Fleer, J. van Male, A. Johner, Macromolecules 32, 825 (1999) & 32, 845 (1999)

13. G.J. Fleer, F.A.M. Leermakers, Macromol. Symp. 126, 65 (1997)

14. A. Silberberg, J. Chem. Phys. 46, 1105 (1967)

15. The polymer adsorption energy parameter can also be expressed in terms of Flory-Huggins type parameters χ_s = (χ_1s - χ_2s) / 6.

16. A.N. Semenov, J. Bonet-Avalos, A. Johner, J.F. Joanny, Macromolecules 29, 2179 (1996)

17. This expression differs by a factor of 1/2 in the tanh function from Semenov et al. expression:¹⁶
    

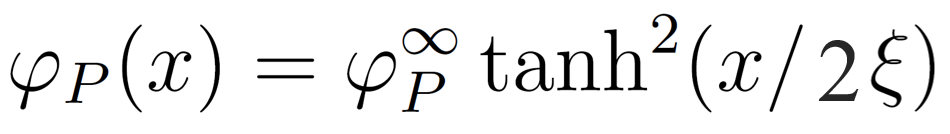
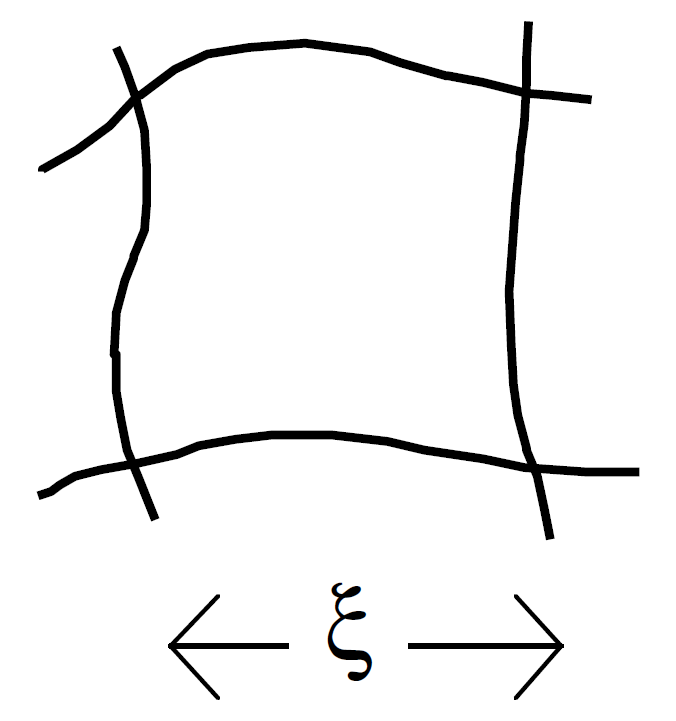
18. A polymer solution resembles a polymer network where the knots or entanglements define the mesh size ξ, which equals the size of a blob in de Gennes scaling model.
    

19. P.G. de Gennes, Macromolecules 14, 1637-1644 (1981) & 15, 492-500 (1982)

20. K.I. Skau, E.M. Blokhuis, and J. van Male, Macromolecules 37, 1969-1979 (2004)