Thermodynamics of Homogeneous Nucleation

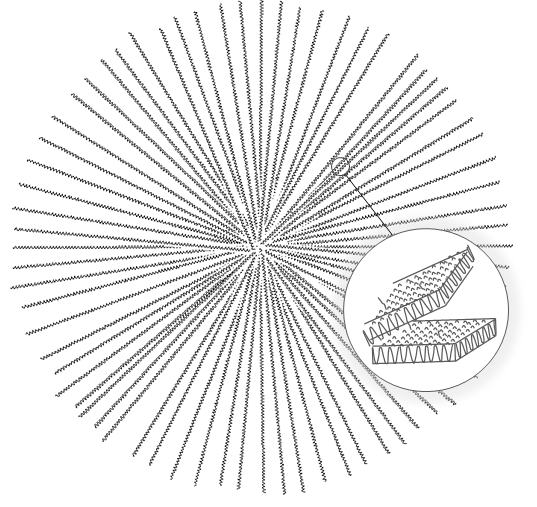
Polymers are known to crystallize from its melt into regular lamellar crystalline structures when cooled below their melting point. The size of these structures can vary from less than one to several hundred angstroms.¹ The formation of these polymer crystals (spherulites) involves two processes that occur spontaneously. The first process is the formation of stable primary nuclei which itself are the result of fluctuations in density of supercooled melts. It is spontaneous below the melting point (T_m,∞) whereas at the melting temperature an equilibrium between liquid and crystals exist as both phases have the same Gibbs s free energy.

ΔG_f = ΔH_f - T_m,∞ ΔS_f = 0

or

ΔT_m,∞ = ΔH_f / ΔS_f

The growth of nuclei requires sufficient mobility which increases with increasing temperature, whereas the rate of nucleation increases with decreasing temperature. Thus, the overall process displays a maximum growth rate somewhere between the melting point and glass transition temperature. Due to the larger rate of nucleation and smaller growth rate, the size of the crystallites (spherulites) decreases at lower temperatures whereas their number per unit volume increases. The lower mobility of the polymer chains at low temperatures also leads to less perfect crystallites (more defects in each lamella).

The nucleation process can be described in terms of excess free energy change; the work required to form a nuclei is equal to the difference between the free energy of the molecules in their molten and crystalline state plus the energy needed to form a new interface between the nucleus and the melt. Assuming spherical nuclei, the excess free energy change may be written

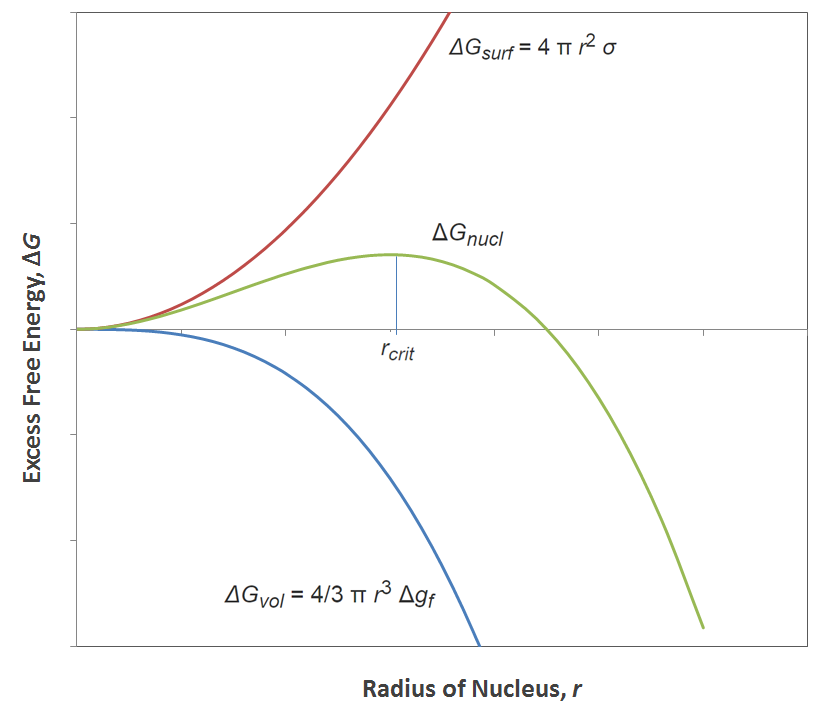
ΔG_nucl = ΔG_vol + ΔG_surf = 4/3 π r³ Δg_f + 4 π r² σ

where r is the radius of the nucleus, Δg_f is the bulk free energy of fusion per unit volume of crystal and σ is the surface free energy.

 

Excess Free energy versus Cluster Size

 

The surface free energy (σ) is usually positive, that is, the formation of a foreign crystal surface is an unfavorable process whereas the free energy change of the crystal (Δg_f) can be either negative or positive depending on the temperature of the polymer because crystallization releases energy but also reduces the entropy of the system. We can distinguish between three temperature regimes:

T > T_m: ΔG_nucl > 0
T = T_m: ΔG_nucl = 0
T < T_m: ΔG_nucl < 0

Crystallization can only occur when ΔG_nucl is negative. However, spontaneous crystal formation and stable growth is only possible if the free energy of fusion ΔG_vol is noticeably larger than the surface free energy ΔG_surf and if

∂/∂r (ΔG_nucl)_T < 0

∂/∂r (ΔG_nucl)_T = 4 π r (r Δg_f + 2 σ)

The graph above shows the total free energy of crystal formation as as a function of cluster or nucleus size. It can be seen that for small cluster sizes, crystallization is an unfavorable process, or in other words, an energy barrier has to be overcome to achieve stable growth starting when the cluster reaches a critical nucleus size r_crit.

r_crit = -2 σ / Δg_f

 

The corresponding energy barrier is

ΔG_nucl(r = r_crit) = -16 π σ³ / 3Δg_f²

Crystallization will only take place in the molten phase at T < T_m and if random thermal fluctuations due to Brownian motion provide enough thermal energy that the molecules can overcome the energy barrier ΔG_nucl. If not, seeds or nucleation agents⁴ need to be present in the molten phase in order to achieve nucleation and spherulitic growth. This process is known as heterogenous nucleation.

The temperature dependence of the energy barrier ΔG_nucl(T) can be calculated when using the definition of the free energy:

Δg_f = Δh_f - T_m Δs_f = Δh_f [1 - T Δs_f /Δh_f]

Assuming that the ratio of Δh_f and Δs_f is constant and equal to the value at T_m, the temperature dependence can be written as

Δg_f = Δh_f [1 - T/T_m]

Using this expression, the critical cluster size r and the energy barrier ΔG_nucl read

r_crit = -2 σ T_m / [Δh_f (T_m-T)]

ΔG_nucl(r = r_crit) = -16 π σ³ T_m³ / [3Δh_f² (T_m-T)²]

Thus, the degree of super cooling (T_m-T) defines the critical size and energy of spontaneous crystallization; the barrier is infinite at the melting point T_m and decreases with decreasing temperature, or in other words, the rate of nucleation steadily increases with decreasing temperature.

References and Notes

1. J.J. Weeks, J. of Res., Vol. 67A, No. 5, pp. 441 - 451 (1963)

2. J. D. Hoffman and J.J. Weeks, J. of Res., Vol. 66A, No. 1, pp. 13 - 28 (1961)

3. J. D. Hoffman and J.I. Lauritzen, J. of Res., Vol. 65A, No. 4, pp. 297 - 336 (1961)

4. These additives create a heterogeneous surface to the polymer melt which has a lower energy barrier. Consequently, the temperature at which the polymer molecules start to crystallize from the melt increases, whereas, at a given temperature, the rate of nucleation and overall rate of crystallization increases. This promotes the formation of smaller and more numerous spherulites which enhances the mechanical properties such as flexural modulus and heat deflection temperature (HDT).
   Nucleating agents are frequently used in polypropylene to improve the molding efficiency and transparency. Some special nucleating agents (known as clarifiers or clarifying agents) produce very small spherulites that do not scatter visible light, thus providing transparent polypropylene.