Gibbs-Thomson Equation
Effect of Crystal Size on Melting Point

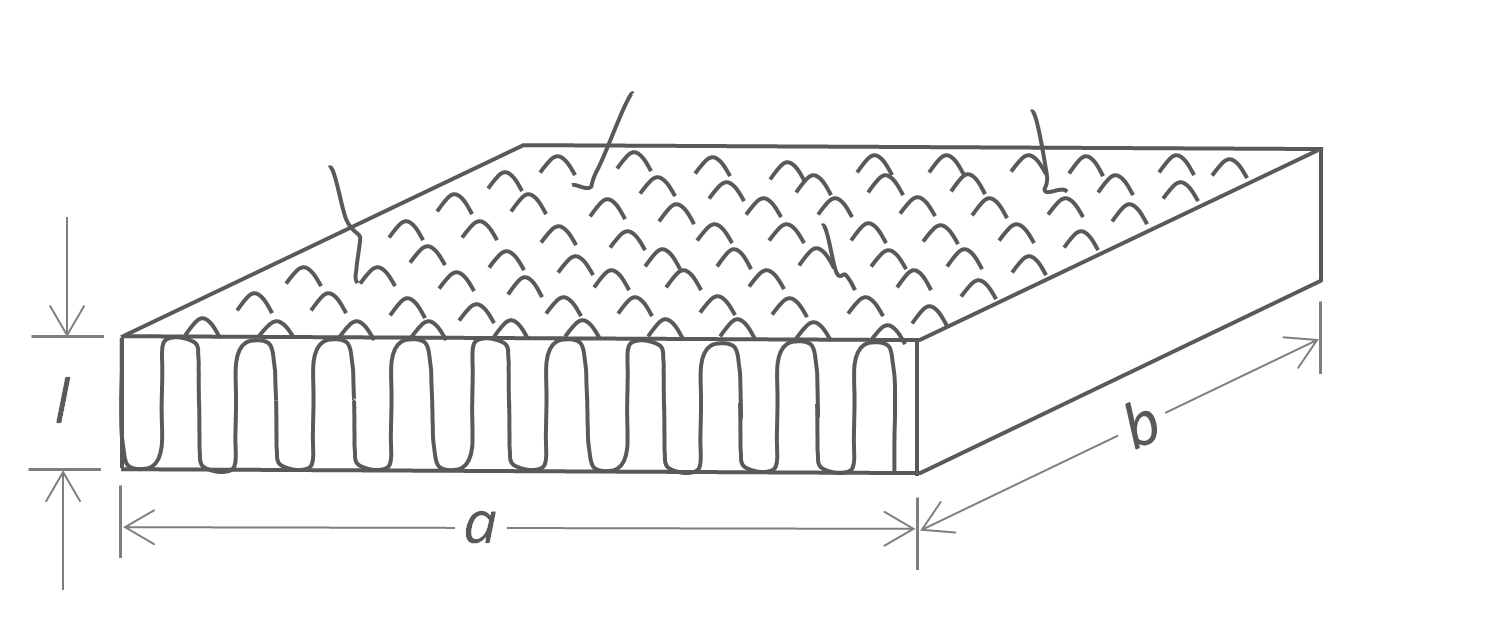
Linear polymers are known to crystallize from their melt into regular lamellar structures when cooled below their melting point. The dependence of the melting point on crystal size can be described with the Gibbs-Thomson equation. A schematic picture of a lamellar crystal is shown below. It is assumed that the thickness l of the lamellae is much smaller than the lateral dimension. The Gibbs free energy of such a lamellae consists of three terms; the first two terms describe the energy necessary to create new surfaces and the third is the bulk free energy of fusion:

ΔG_lam = 2abσ_e + 2l (a+b) σ - abl Δg_f

where σ and σ_e are the surface free energy of the lateral and end surfaces of the lamella (see Figure below). Both σ and σ_e are considered constants that are difficult to measure or to calculate, that is, usually only estimates exist. In many cases, l « a,b, so that the contribution of σ to the crystal energy can be neglected in good approximation,

ΔG_lam  ≈ 2abσ_e - abl Δg_f

At the melting point of the crystal, ΔG_lam = 0, thus

Δg_f ≈ 2σ_e / l

Lamellar Crystal with Chain folds

The free energy of fusion involves both an enthalpic and entropic change

Δg_f  = Δh_f - T Δs_f

Assuming Δs_f and Δh_f show only a small temperature dependence, both quantities have values very similar to those of an infinite large crystal which melts at T_m,∞:

Δh_f(T_m,∞) ≈ Δh_f(T_m)
Δs_f(T_m,∞) ≈ Δs_f(T_m)

Thus

Δg_f(T_m) ≈ Δh_f(T_m,∞) (1 - T_m/T_m,∞)

Which can be rewritten to give the Gibbs-Thomson relation:^1,2

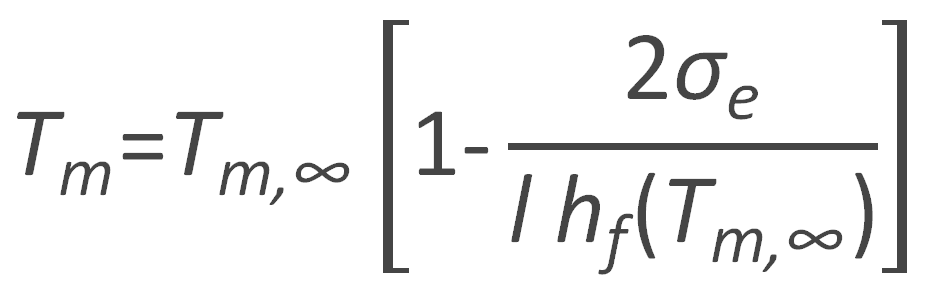
or

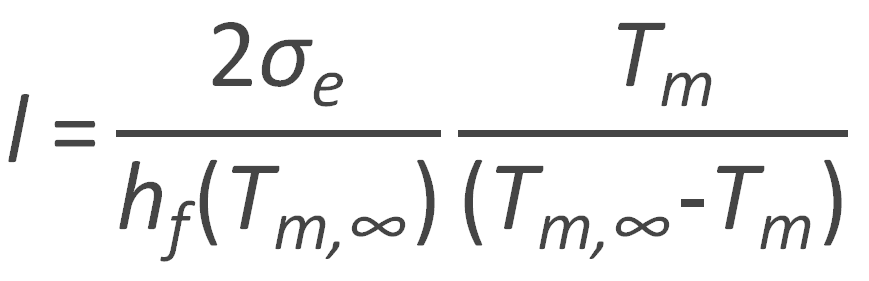
This equation allows for the prediction of the melting point T_m as a function of the lamellar thickness l. If, on the other hand, both the melting temperature of an infinite large and that of the actual crystals are known, the free energy σ_e can be calculated, for example by plotting the observed temperatures versus the reciprocal lamellar thickness 1/l (see Fig. below).

 

Gibbs-Thomson Plot

 

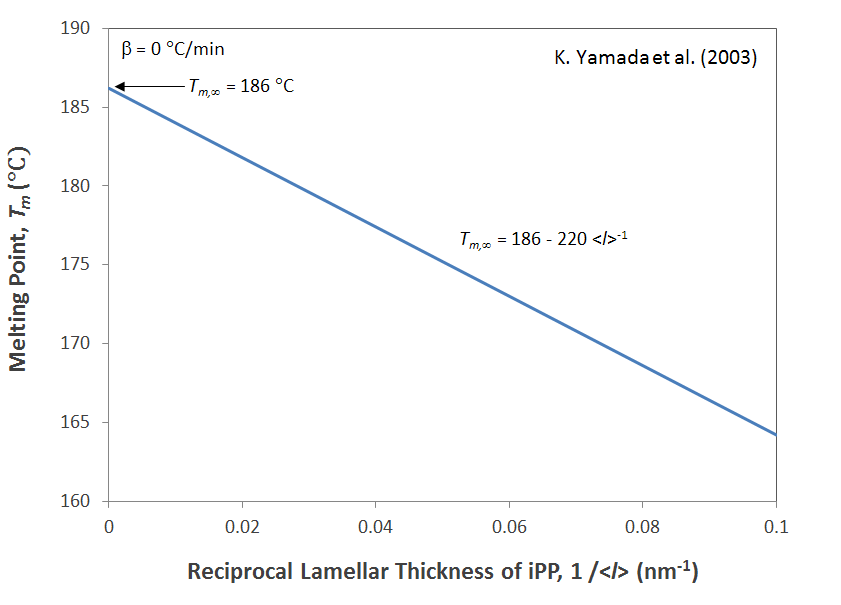
The Gibbs-Thomson equation has been applied to many linear polymers such as isotactic polypropylene and polyethylene. It was shown to give reliable predictions of the melting point as a function of lamellar thickness.⁴

Another important relation has been derived by Hoffman and Weeks (1962).² Their expression relates the observed melting point T_m,obs of a polymer to its crystallization temperature T_c and equilibrium melting point T_m,∞. To obtain these temperatures, a polymer specimen is crystallized isothermally at T_c after being cooled from its melt which is then subsequently heated at a specified rate until all traces of crystallinity have disappeard which defines T_m,obs. The experiment is then repeated for different T_c values. Hoffman, Lauritzen, and Weeks^2,3 found that the curves of T_m,obs versus T_c can be describes with following simple relation:

T_m,obs ≈ T_m,∞ (1 - 1/γ) + T_c /γ

The equilibrium melting point is the intersection of these lines with the line T_m,obs = T_c.² and the parameter γ is the thickening coefficient as determined by the Hoffman-Weeks plot.

 

Hoffman-Weeks Plot

 

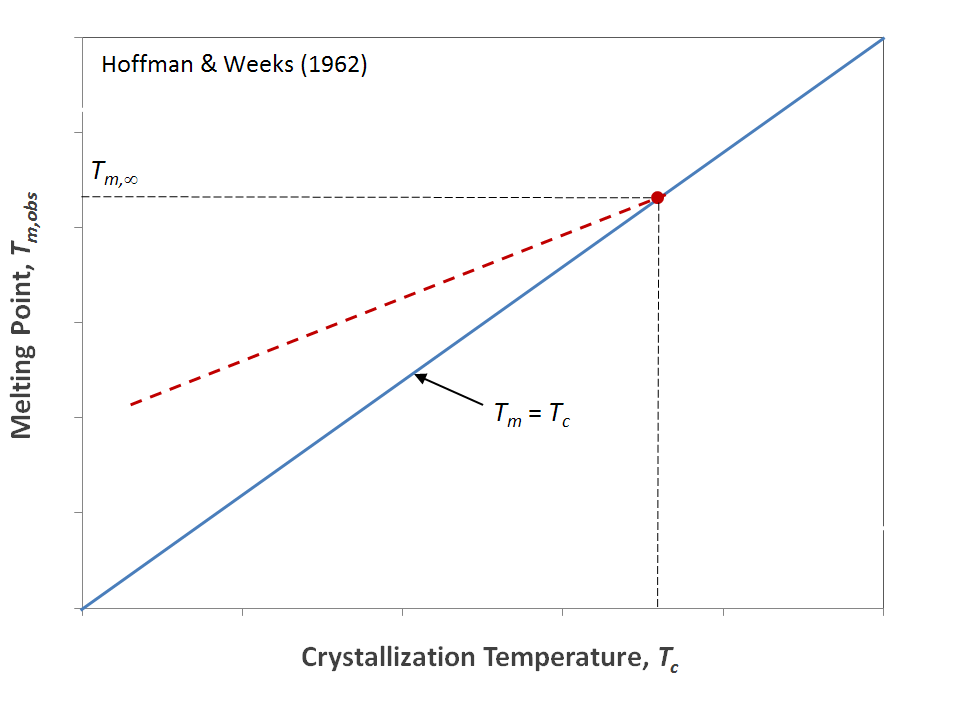
The Hoffman-Weeks method is widely used to estimate melting points of polymers. However, Yamada et al. found that this method is not always reliable.⁴

References

1. J.J. Weeks, J. of Res., Vol. 67A, No. 5, pp. 441 - 451 (1963)

2. J. D. Hoffman and J.J. Weeks, J. of Res., Vol. 66A, No. 1, pp. 13 - 28 (1961)

3. J. D. Hoffman and J.I. Lauritzen, J. of Res., Vol. 65A, No. 4, pp. 297 - 336 (1961)

4. K. Yamada, M. Hikosaka, A. Toda, S. Yamazaki, and K. Tagashira, Macromolecules,
   36, 4790-4801 (2003)