Polyelectrolytes in Solutions
Polyelectrolytes are polymers carrying ionizable groups in their repeat units. They can be divided into polycations, polyanions and polysalts. Like ordinary electrolytes (acids, bases and salts), the ionizable groups dissociate in aqueous solutions (water), forming ions on the chain and counterions in the solution. Thus, the properties of polyelectrolytes are similar to both electrolytes and polymers.
Examples of polyelectrolytes include sodium polystyrene sulfonate, polyallylamine hydrochloride, polydiallyldimethyl ammonium chloride, polyvinyl pyridine, anionic polyacrylamide, polyacrylic and polymethacrylic acids and their salts, carboxymethyl cellulose and their salts and DNA.
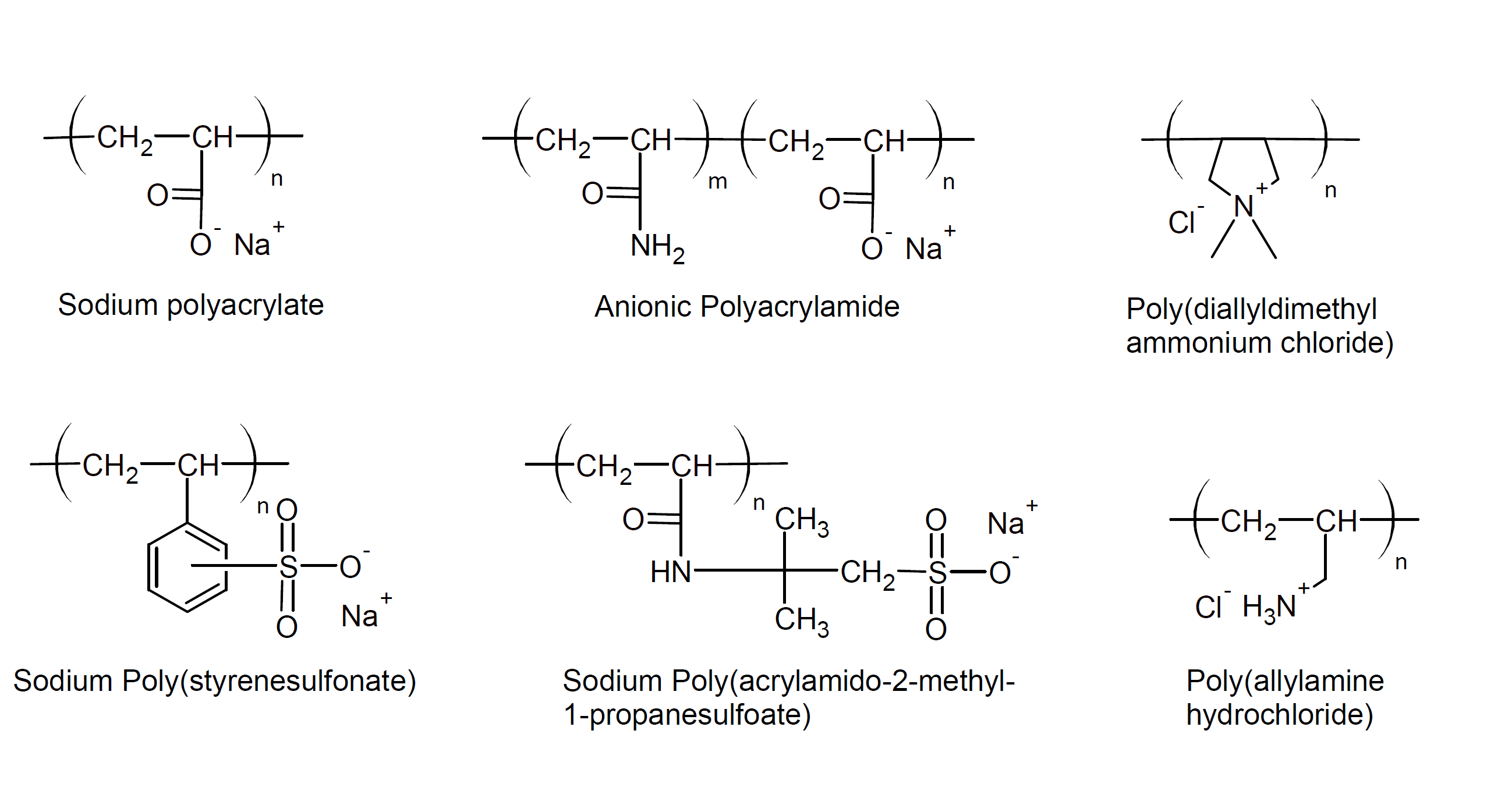
The properties of polyelectrolyte solutions are very different from those of solutions of uncharged polymers. For example, the viscosity η of dilute polyelectrolyte solutions is proportional to the square root of polymer concentration η ∼ c½, whereas the viscosity of solutions of uncharged polymers in the same regime is proportional to the concentration η ∼ c.1,2 Another property that differs markedly from neutral polymers is the osmotic pressure; due to the presence of counter-ions, the osmotic pressure in salt-free solutions is comparable to the osmotic pressure produced by low molecular weight solutions, which is much higher than that of solutions of neutral polymers. In other words, the main contribution to the osmotic pressure of polyelectrolyte solutions results from the counterions.
The counter-ions of a charged polyelectrolyte in a salt-free solution are mostly located near the chain. Due to strong attractive coulomb forces, a portion of them is kept as a (solvated) condensate in close vicinity of the polyions. These ions strongly screen the Coulomb interactions between charges. The minimum distance between effective charges along the polymer backbone is known as the Bjerrum length,4 which is typically much larger than the length of a monomer. If salt is added to the polyelectrolyte solution, the Coulomb forces become partially screened so that fewer counter-ions are condensed.
Counterion Condensation
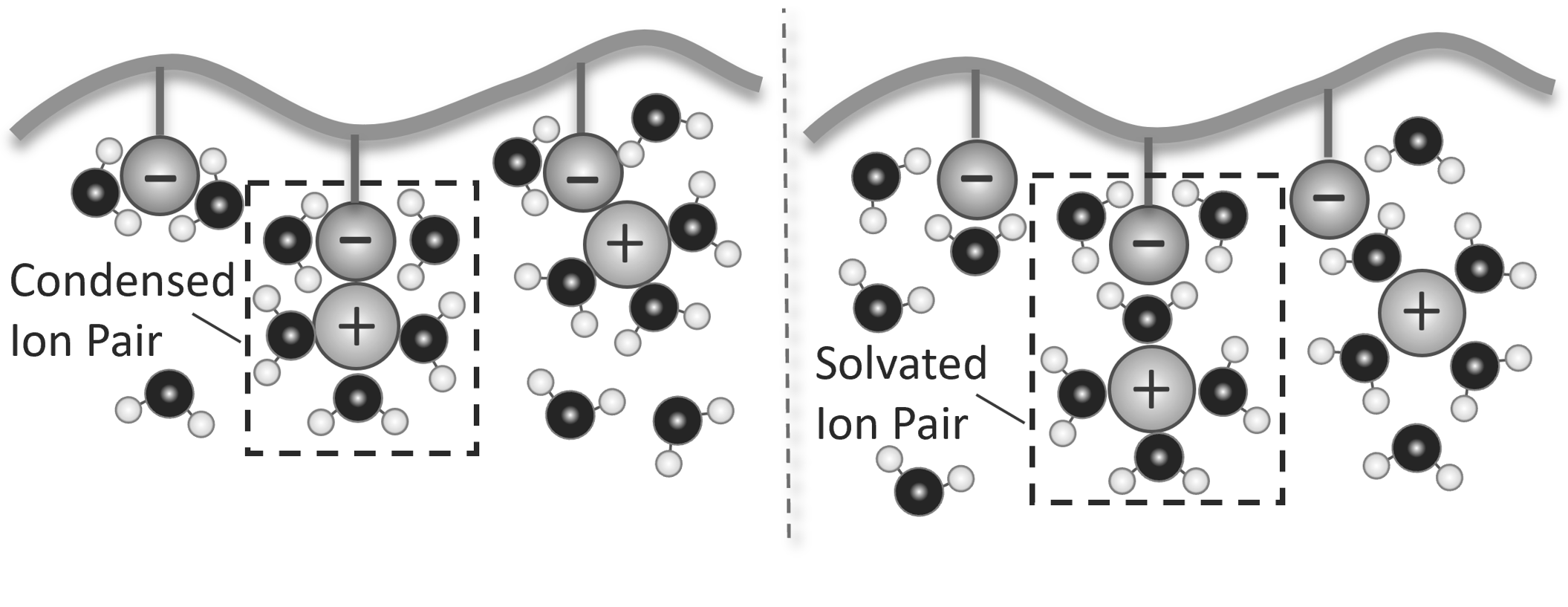
Counterion Condensation
The cloud of counter-ions around charged particles partially screens the particle charge and at a certain distance the Coulomb forces practically vanish. This critical distance is known as the Debye length.5-6 It varies with the ionic strength of the mobile ions, which in turn, depends on the type of ions and their concentration in solution. As will be shown below, the Debyle length scales inversely with the square root of the ionic strength.
Rod-like Polyelectrolytes and Bjerrum Length
Charged polyelectrolytes in a salt-free solution are almost fully extended due to the strong repulsive forces between the charged links along the polymer backbone. Such a rod-like polymer of radius r0 will develop an electric field similar to a thin linear wire with linear charge density e/l0. The corresponding electrostatic potential and energy at distance r from the chain axes is given by3,7
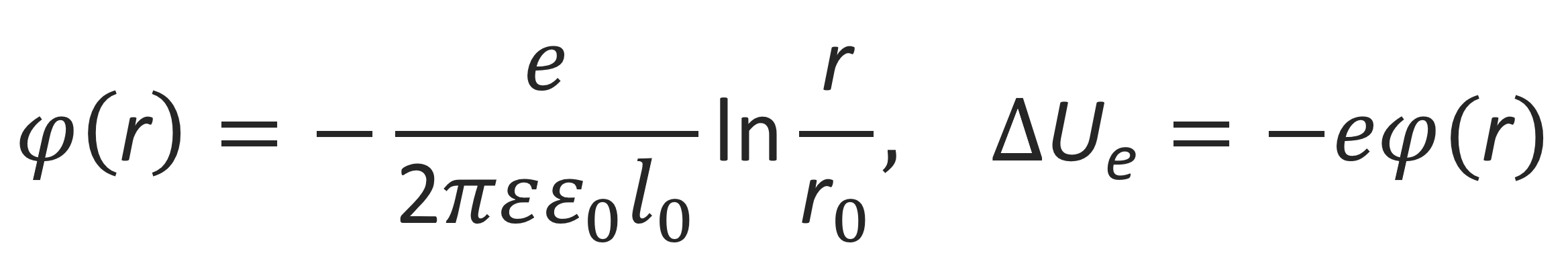
where e and ε are the elementary charge and dielectric constant of the medium, respectively. The rod-like polyions will be surrounded by a cloud of counterions. Their spatial distribution will depend on the electrostatic force field that surrounds the rod-like polyions and the temperature T. At low temperatures and high linear charge densities, a large portion will stay in the immediate vicinity of the chain, whereas at high temperatures and low charge densities they might diffuse away.
To solve this problem, the space around the charged polyion rod is divided into a series of cylindrical cells i of thickness Δr and inner radius ri. The probability that an ion occupies a cell i can be calculated from its free energy:
![]() ,
,
where ΔUe,i and ΔSe,i is the electrostatic energy and entropy in cell i, respectively.
Rod-like Polyion with radius r0
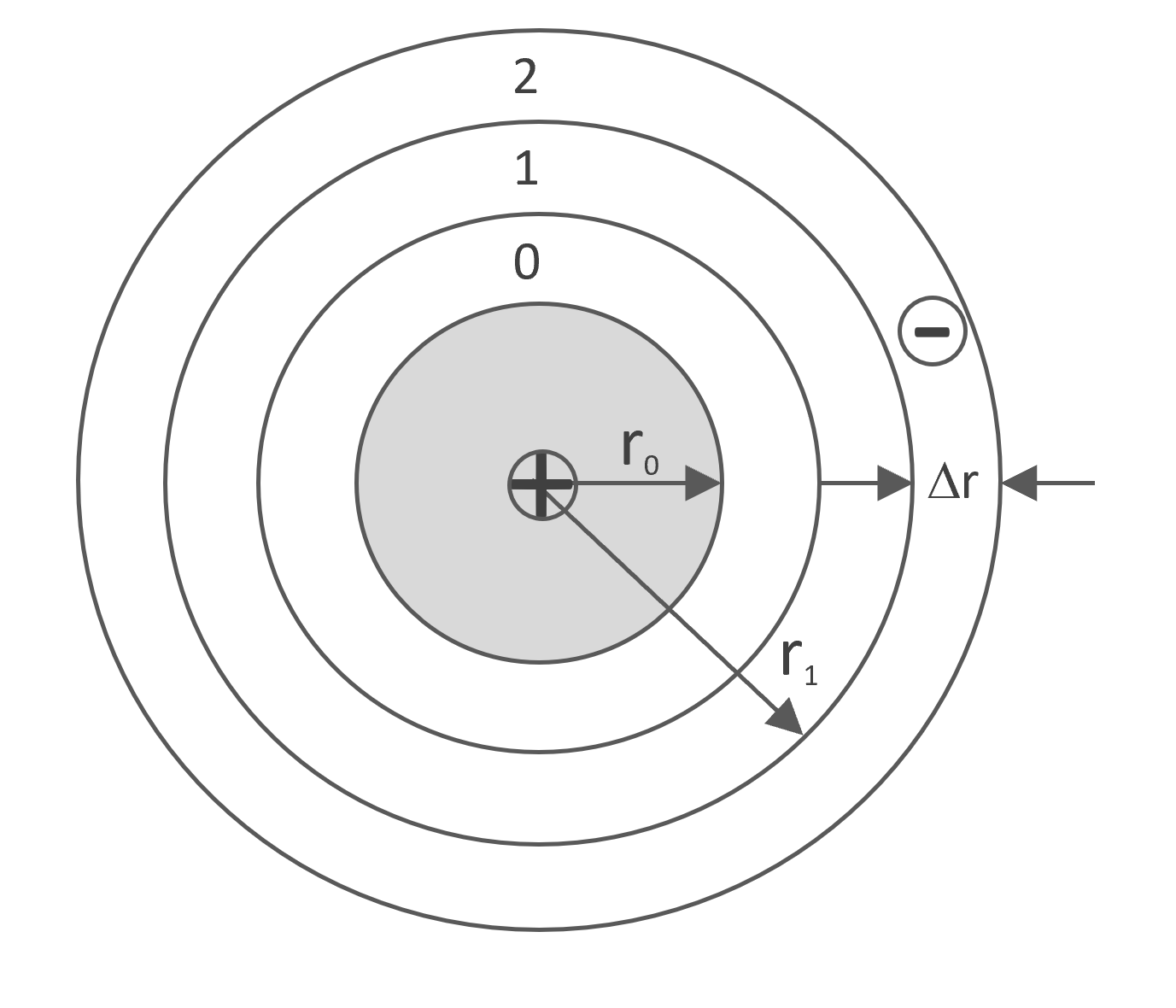
Rod-like Polyion with radius r0
The change in entropy when moving a counterion from the first cell i = 0 to an outer cell i > 0 is given by3,9
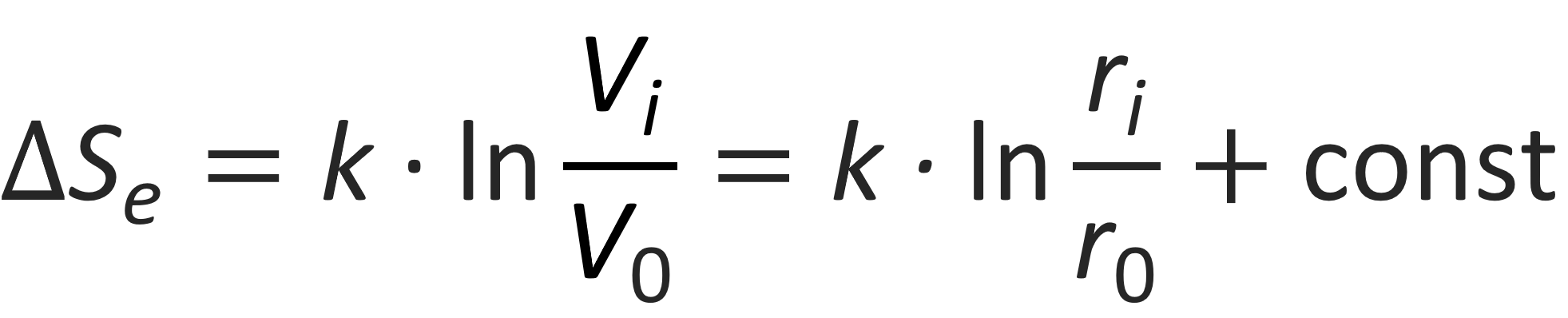
Then the change in free energy can be written as3
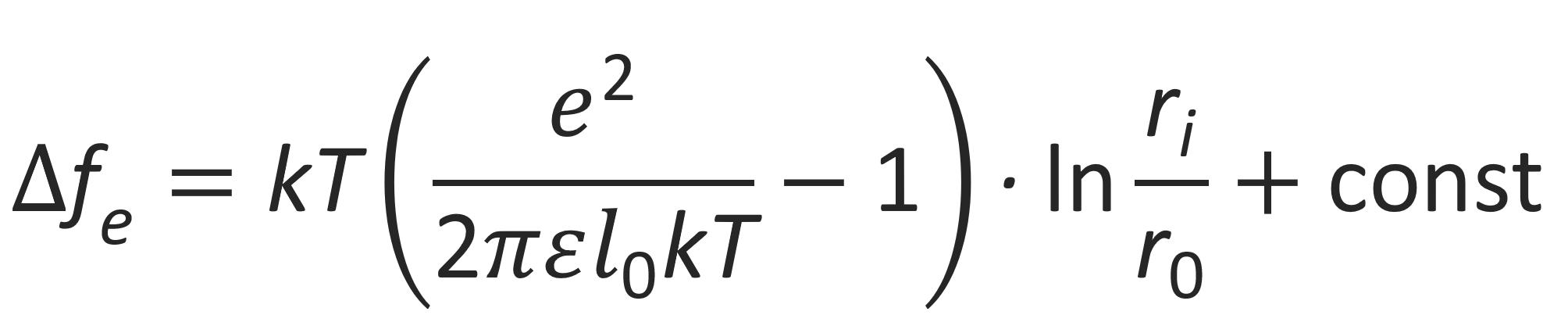
or
![]()
Assuming many non-interacting counterions, the distribution of ions over the cylindrical cells can be predicted using Boltzmann statistics:
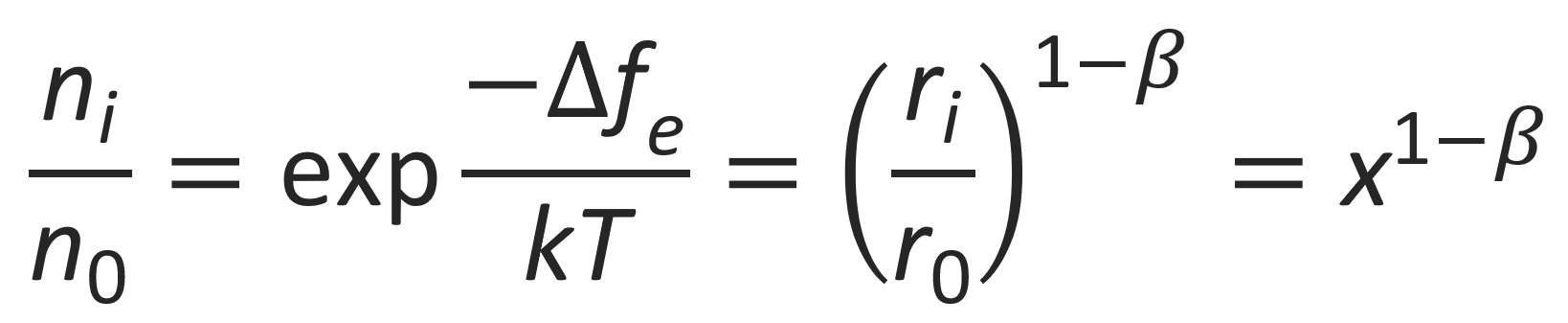
Then the average number of counterions in the first cell (i.e. the ions in the condensed state) is given by
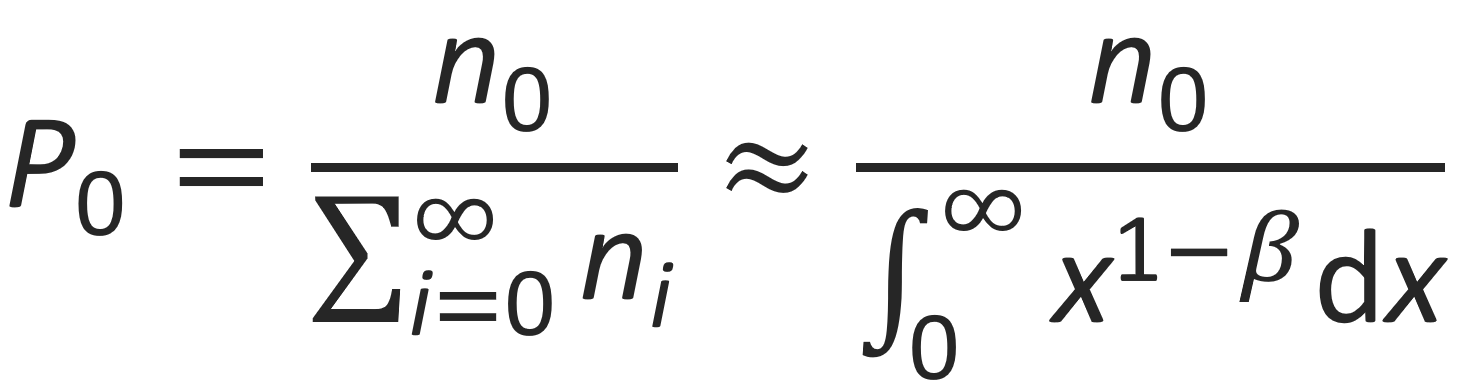
The integral in the denominator diverges for β ≤ 2. Then P0 becomes zero, which means counterions do not condense at the chain surface, while for β ≥ 2, the integral remains finite and counterions accumulate at the the polyion surface. Thus β = 2 is a critical value for counterion condensation:3,8
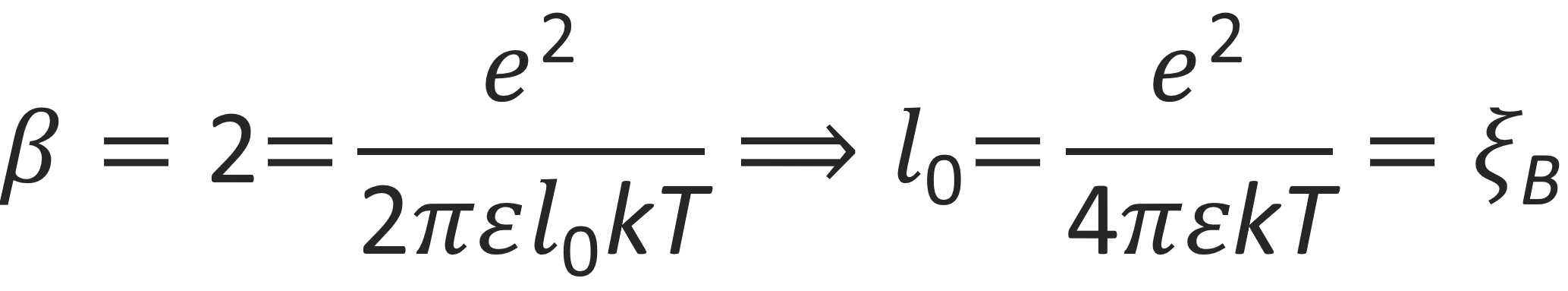
The parameter ξB is the so-called Bjerrum length. If the distance between neighboring charges on the polymer backbone becomes larger than ξB, the kinetic energy will exceed the electrostatic energy and the counter-ions will diffuse away. If, on the hand, the distance between neighboring charges is smaller than ξB, a portion of the counter-ions will remain in the immediate neighborhood of the polyions.2,3
Debye-Hueckel Theory of Charge Screening
Due to long-range Coulomb forces, charged particles are typically surrounded by a cloud of opposite charged ions which lower the electrostatic energy. In a similar way, counterions will accumulate near a charged polyelectrolyte which reduces and shields its net charge. The distribution of mobile counterions in the ion cloud can be described with the Poisson-Boltzmann distribution. According to this equation, the charge density ρα(r) of counterions of type α with valence zα at an arbitrary location r (distance from the chain axes) will depend on the electrostatic potential φ(r) and the temperature T:
![]()
where cα,∞ is the number density of counterion species α at large distances from the central cation. The potential, in turn, is determined by the charge distribution around the polyelectrolyte. In other words, the field needs to be self-consistent. This is the case when the charge distribution satisfies the Poisson equation:
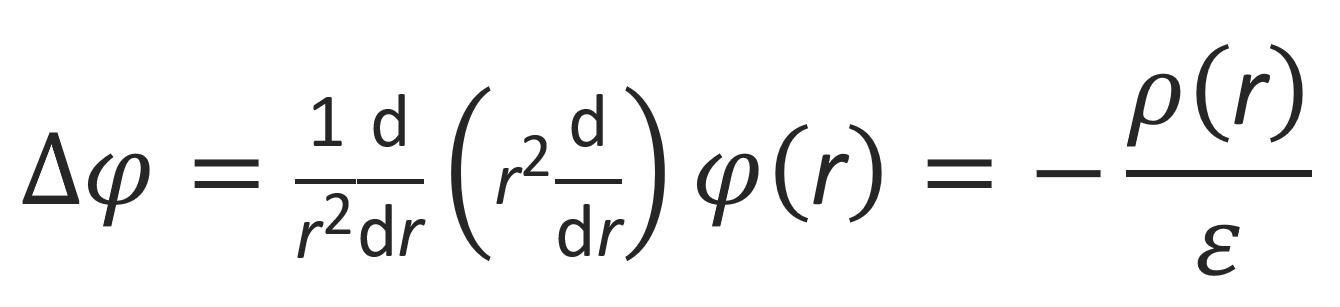
The charge density ρtot(r) at each point has a contribution from the polyion and the fluctuating counterions:
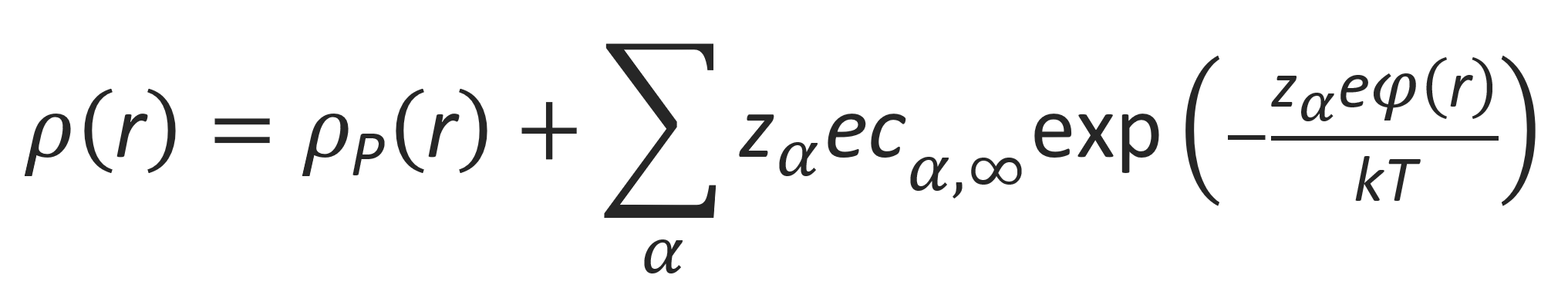
Then
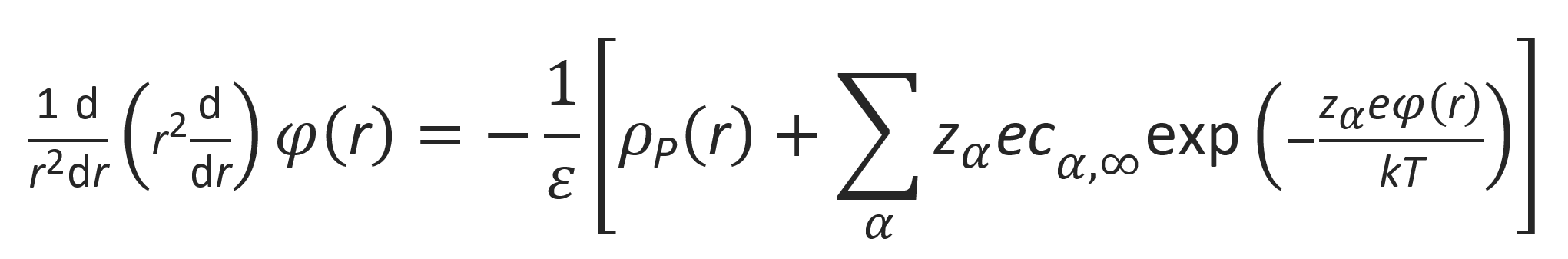
This equation is known as the Boltzmann-Poisson equation. It is a non-linear partial differential equation which is difficult to solve. To simplify the problem, the exponentials are often linearized:
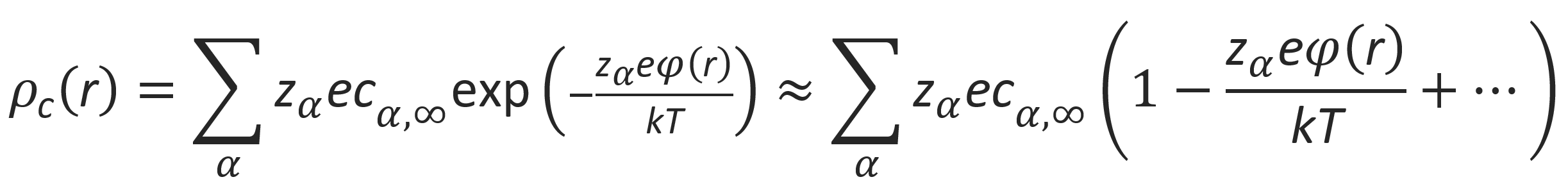
In the presence of salt, the mobile ions are a mixture of cations and anions formed by dissociation of salt and polyions. If the concentration of polyions is very low compared to that of salt, its contribution to the total ion content may be neglected. Then the linear term in the above equation vanishes and the Poisson-Boltzmann equation reduces to
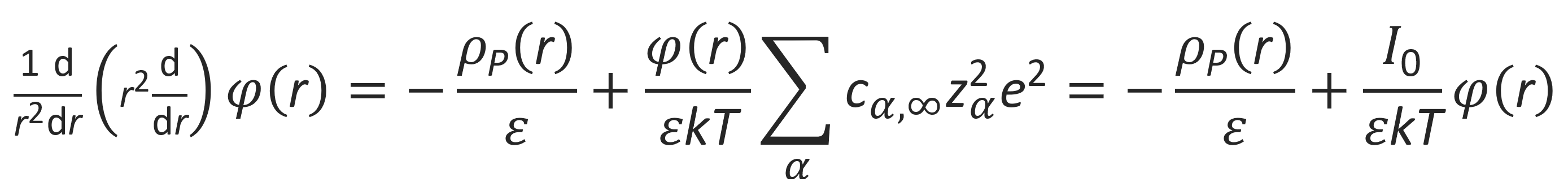
where I0 is referred to as the ionic strength. This equation can be rewritten as
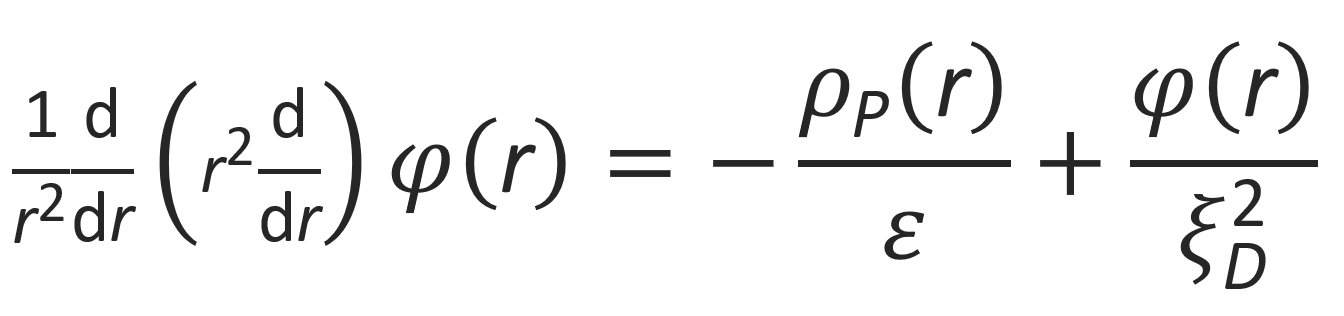
where
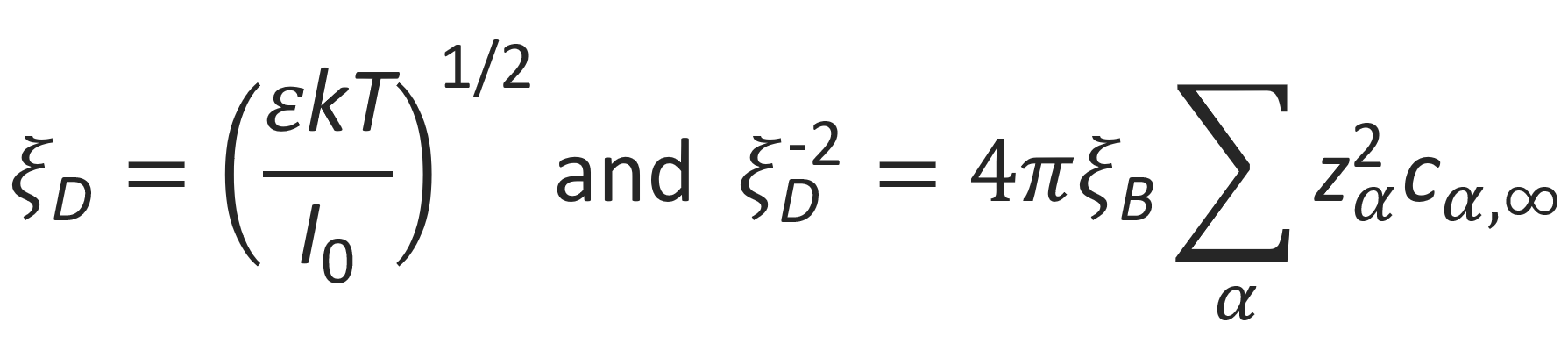
is the Debye screening length. This so-called Debye-Hueckel equation can be exactly solved. For a single point-like central charge ze with ρp = ze δ(r), the general solution is3,8
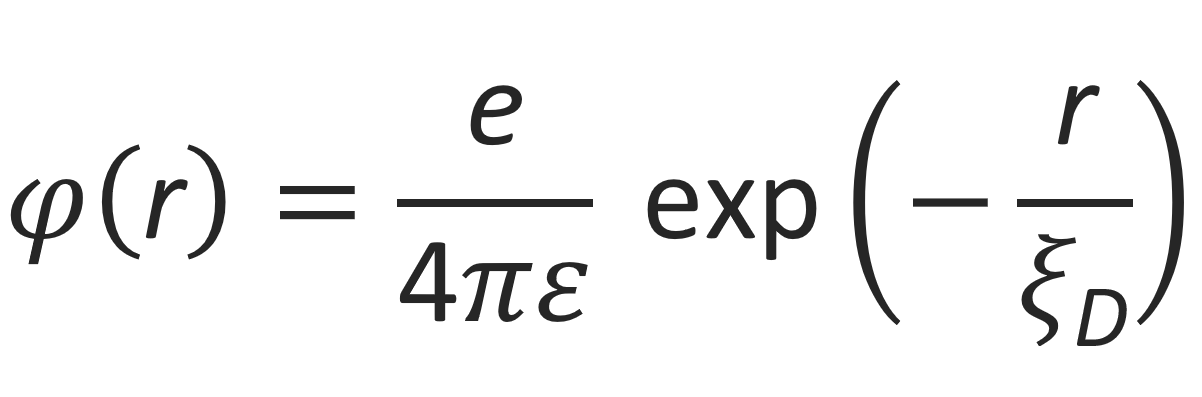
The screened coulomb interaction energy of the electrolyte solution Ue,tot is equal to the sum of all pairwise interaction energies between ions of charges zme and zne(8)
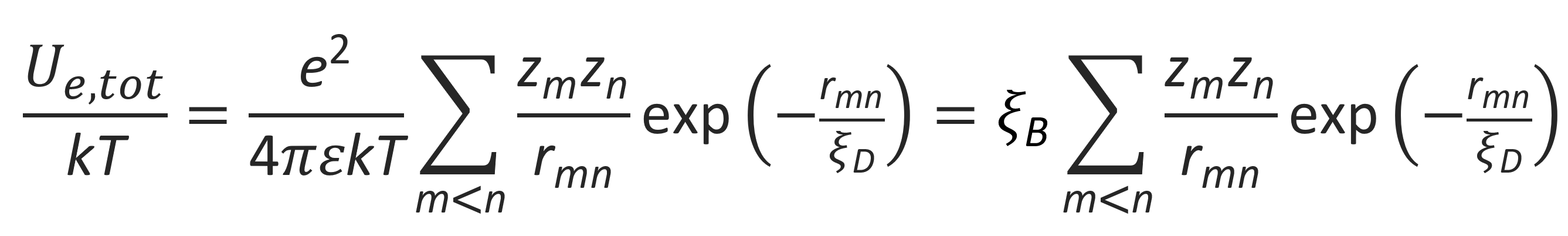
Note, that the Debye-Hueckel approximation is not applicable to solutions with low salt content.
Rod-like Polyions & Wormlike Chain Model
Strongly charged polyelectrolytes can be treated as wormlike chains, i.e., as slightly bended thin cylinders. This model is a satisfactory description of a real polyelectrolyte as long as the Debye-Hueckel screening length ξD is less than the persistence length lp. The stiffness of such a chain decreases with increasing ionic strength because the electrostatic repulsion between charged groups along the chain becomes more shielded by the salt ions.
The theory of wormlike polymers was extended to polyelectrolytes independently by Odijk and by Skolnick and Fixman in 1977, who calculated the electrostatic persistence length by neglecting excluded volume effects and assuming a continuous, uniform charge distribution. They showed that the persistence length of a polyelectrolyte chain can be written as a sum of the regular persistence length lp and the electrostatic persistence length lp,el:12-14
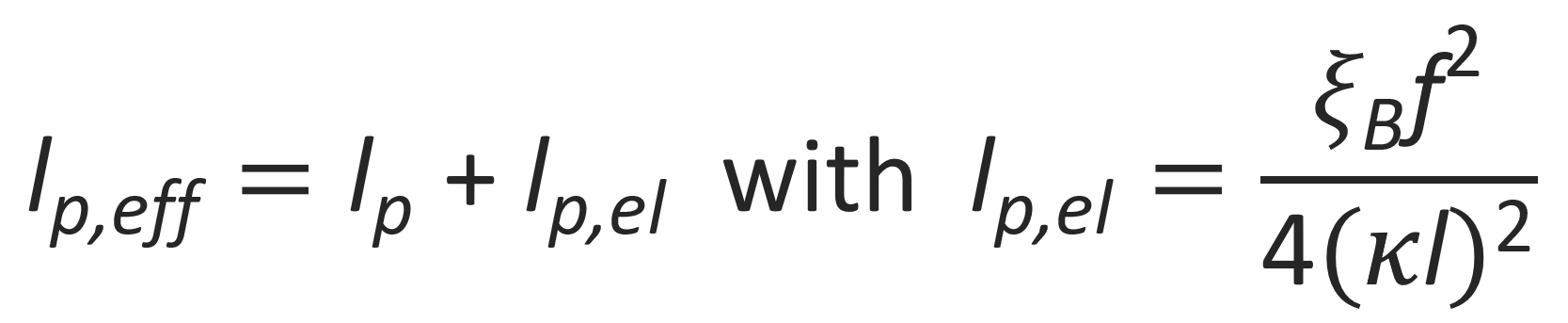
where l is the bond length, κ the inverse Debye screening length, and f the fraction of charged monomers in salt solution. This equation shows that the stiffness of the chain can be adjusted by varying the salt concentration. Furthermore, for salt-free conditions (κ → 0), the electrostatic persistence length will be very large.
References & Notes
- R. M. Fuoss, Discuss. Faraday Soc., 11, 125 (1951)
- A.V. Dobrynin, R.H. Colby and M. Rubinstein, Prog. Polym. Sci., 30 1049-1118 (2005)
- G. Strobl, The Physics of Polymers, 3rd Edition, Heidelberg 2007
The Bjerrum length was named after the Danish chemist Niels Bjerrum (1879-1958). It is the separation length between charges at which the electrostatic potential energy between two charges is comparable in magnitude to the thermal energy, kT.
- A.V. Dobrynin, R.H. Colby and M. Rubinstein, Macromolecules 28, 1859-1871 (1996)
The Debye length was named after the Dutch-American physicist and chemist Peter Debye (1884-1966). It is a measure for how far the electrostatic field of a charged particle reaches. In other words, beyond ξD, the electrostatic effect is screened by the mobile charges.
- P.A. Tipler, Physics, Spectrum, Heidelberg, pp. 697-698 (1994)
- M. Muthukumar, Macromolecules, 50, pp. 9528-9560 (2017)
Note, G. Strobl chose as the reference state the cylinder volume of the polyion rod:3
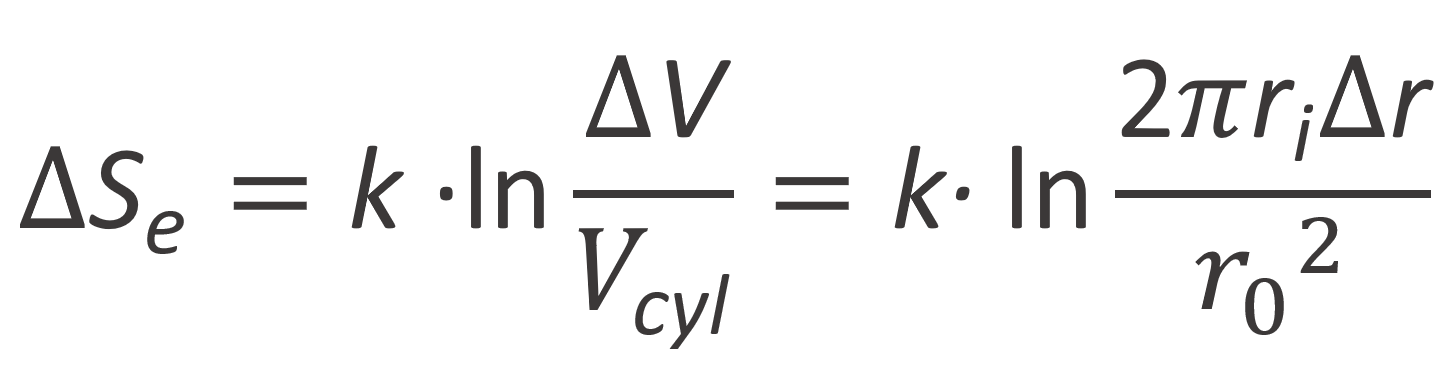
- P.G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, NY, 1970
- A. Y. Grosberg, A.R. Khokhlov, Statistical Physics of Macromolecules, AIP Press, NY 1994
- T. Odijk, J. Polym. Sci., Polym. Phys. Ed., 15, 477-483 (1977)
- J. Skolnick and M. Fixman, Macromolecules, 10 (5), 944-948 (1977)
- A.V. Dobrynin, Macromolecules, Vol. 38, No. 22, 9304-9314 (2005)