Links:

Dielectric Properties
of Polymers

Polymers have long been known as insulating materials and are often used to insulate cables and electrical devices. They are also called dielectrics. Traditionally, dielectric materials are made from inorganic materials such as porcelain, mica, and quartz. However, polymers are also used as dielectric materials. They have the advantage that they can be easier processed, are flexible, cheaper, and can be better tailored for specific applications. They also have excellent chemical resistance. Some disadvantages of polymeric materials are their much lower upper service temperature, their susceptibility to atmospheric and hydrolytic degradation and their flammability. They also have a much larger coefficient of thermal expansion compared to ceramic materials.

An important property of an insulator is its relative permittivity or dielelectric constant (ε). It describes the tendency of a material to polarize in response to an applied electrical field. It is a dimensionless parameter, defined as the ratio of the external (applied) field E₀ (the field without the dielectric) to the electric field inside the dielectric, E:

ε = E₀ / E

The field inside the dielectric, E, is the vector sum, E = E₀ + E_p, of the external field E₀ and the field E_p caused by the substance polarization P

E_p = - P / ε₀

where ε₀ is the permittivity of the vacuum. The polarization is usually proportional to the macroscopic field, particularly if the field is weak:

E_p = - χ E,

or

ε = 1 + χ

χ is the macroscopic susceptibility of the dielectric which is another dimensionless parameter that depends on the material.

The dielectric properties (susceptibility, polarizability, permittivity, etc.) of any polymer depend on its chemical composition and structure. Non-polar plastics with a symmetrical structure and truly covalent bonds are the best insulators. Since there are no dipoles present in the repeat units, an applied field cannot cause any dipoles to allign in field direction which would weaken the electrical field. Most other plastics have polarized covalent bonds, that is, the electrons are drawn closer to the more electronegative atoms. These dipoles will orient themselves to lign up with the electrical field which results in a much stronger polarization and a higher relative permeability (dielectric constant) and lower resistivity compared to non-polar polymers.

 

Relationship between Permittivity and polarization

The polarization of a dielectric material, P (C/m²), is defined as the dipole moment per unit volume. On a microscopic scale, the degree of polarization depends on the polarizability of the molecules (repeat units) and the local electric field, E_loc,

P = Σ_i n_i α_i E_loc

where α_i is the polarizability of a structural element i and n_i is its concentration (number of structural elements i per unit volume),

The relationship between the polarization, P, and the applied electric field E is

P = ε₀ E (ε - 1)

And the relationship between the local field, E_loc, and the polarization, P, is

E_loc = E + P / (3 ε₀)

Combining all three expression gives the Clausius-Mosotti relation:

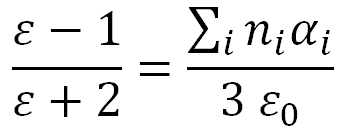
The total polarization associated with atoms, ions, and molecules has four different contributions:

1. Electronic polarization due to displacement of the local electronic charge clouds around each nucleus by the electric field

2. Atomic polarization due to small displacements of the atomic nuclei within the molecules

3. Ionic polarization in ionic materials due to displacement of cations and anions in opposite directions

4. Orientational polarization due to alignment of permanent electric dipoles

The polarizable elements, which are either of electronic, atomic or dipolar nature, contribute only to the permittivity up to a certain frequency depending on the mass of the charged particles and bond type. For example, at frequencies in the visible and ultraviolet range, only the very low mass electrons can follow the applied oscillating electric field whereas the atomic polarization of the heavier and slower moving nuclei tapers off above infrared frequencies. The orientation polarization of permanent dipole moments is particularly “sluggish” and requires much more time than electronic and atomic polarization. It typically occurs only at frequencies at microwave or lower frequencies.

The contribution of each type of polarization to the overall dielectric constant (rel. permittivity) is usually additive

ε = ε_electronic + ε_atomic + ε_dipolar

At optical frequencies, where only electronic polarization contributes to the permittivity, ε can be related to the refractive index, n, by Maxwell's identity:

ε = n²

Thus, the refractive index can be used to determine the electronic polarization and polarizability.

 

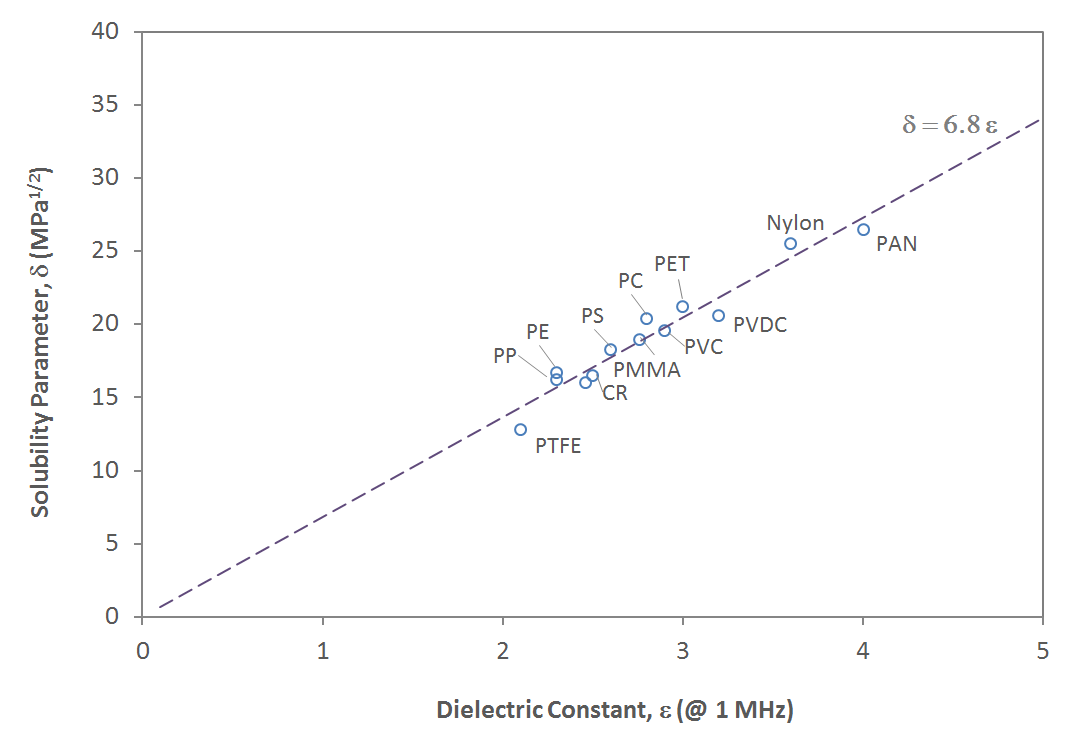
Correlation between dielectric constant and cohesive energy

Since the electrical forces due to polarizability and polar moments determine the cohesive energy, a correlation between the dielectric constant and the cohesive energy (or solubility parameter) can be expected. The relationship between these two parameters is shown in the figure below. It appears that a simple linear correlation exists:

δ ≈ 6.8 ε

 

 

• Both the atomic and orientational polarization depend on the temperature and field frequency whereas the electronic polarization is more or less independent of the frequency and shows a much weaker dependency on the temperature.

• Atomic polarization occurs in all types of polymers even in those with no permanent dipole. It is more able to follow the oscillating electric field than orientational polarization but is not instantaneous and its contribution to the overall permittivity is rather small when compared to electronic polarization.