Model Potentials of
Off-Lattice chains

Polymers, also called macromolecules, are made up of a large number of molecular units linked together by covalent bonds. The repeating units are organic in most cases, for example -CH₂- or -CH₂-O-. These units can also be copolymerized, so that a large variation in the chemical structure can be achieved. The simplest polymer is polyethylene which consists of methylene-groups linked to each other. Due to its internal flexibility, it can arrange in a huge number of different shapes (conformations). Basically, the number of degrees of freedom of the macromolecule is three times the number of atoms. The internal motion of the atoms in a polymer chain can be split into two different types. The first type includes vibrations of bonds and of bond angles, These vibrations affect only the microscopic structure of the polymer chain but do not affect the overall form (conformation) of the chain. The second type of motions are rotations around the C-C-bonds which can convert a stretched chain into a coiled one and are in general responsible for all the transitions between the different conformational states. The chemical nature of the polymer chain determines the forces between neighboring monomers and therefore the conformational energy changes associated with the rotation and vibration of the repeat units. But there are also interactions between monomers that are separated by many bonds along the chain, and of course between monomers of different chains. These interactions are usually represented by a Lennard- Jones potential and are much more complicated than the pair potentials for simple fluids. Thus, even for the simple polyethylene chain, a complicated Hamiltonian with many different parameters results.

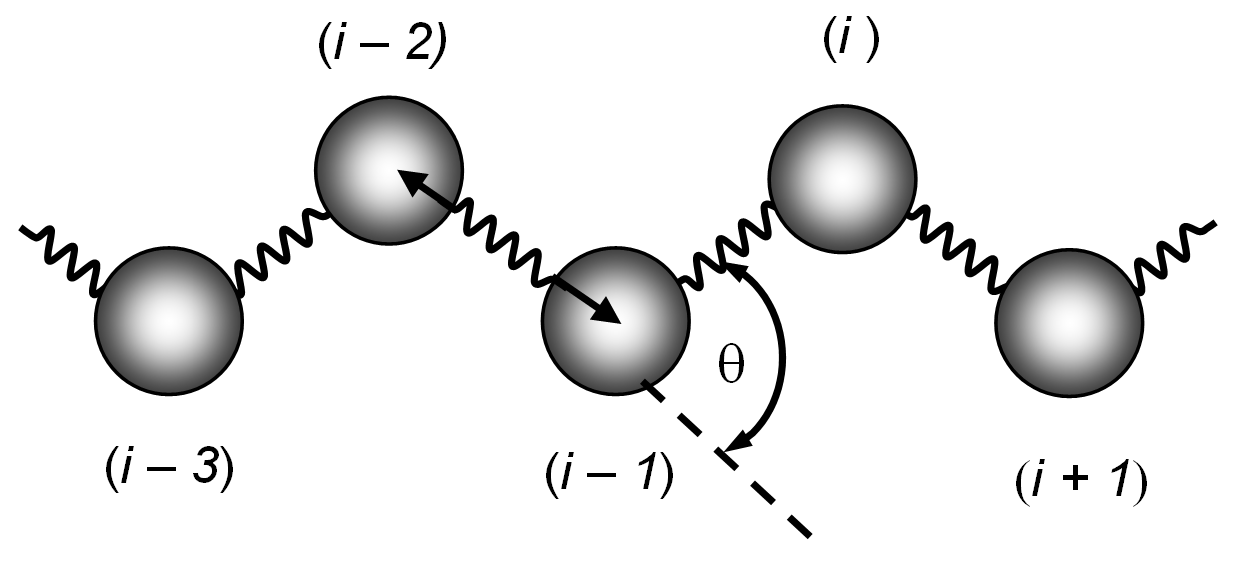
An exact treatment of the physical properties of a large polymer therefore seems to be impossible. This is why scientist often use a coarse-grained model for polymer chains. A very popular model ignores the hydrogen atoms of the CH₂-groups and replaces them with united atoms.² Neither the bond angle nor the bond length are treated as rigid, so the Hamiltonian is still very complicated:³

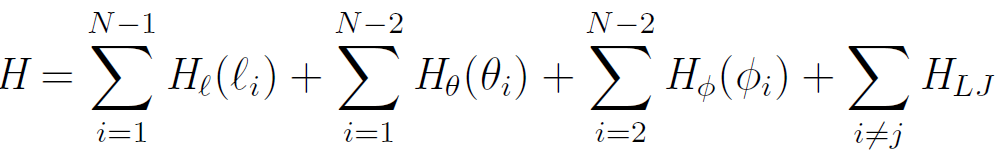
For the bond length and bond angle vibration, a harmonic potential is often assumed:

where l₀ and and θ₀ are the equilibrium bond length and valence angle for which the potential energy has its minimum (usually set zero). The potential associated with the rotation of the C-C-bond is described by a threefold torsional potential:

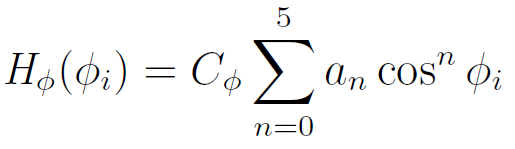
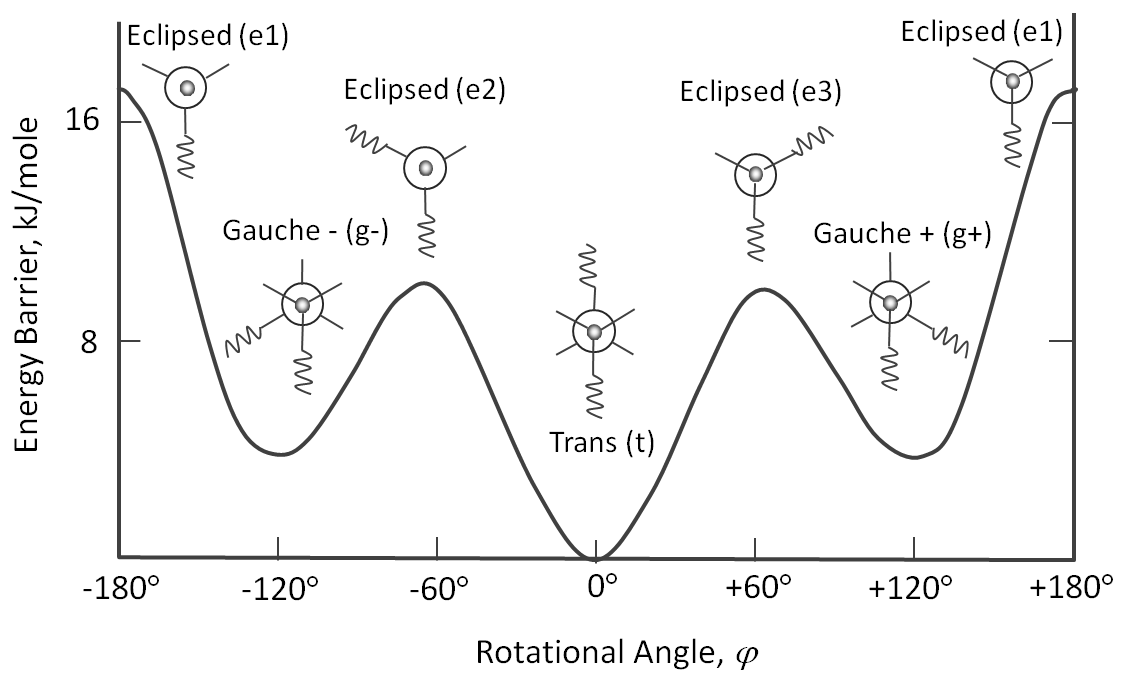
The rotational states are often further simplified by considering only trans, gauche+, and gauche- which are assigned to those bonds having dihedral angles in the range -60° to +60° (0°), +60° to +180° (+120°), and -180° to -60° (-120°), respectively.

 

Finally, the nonbonded interactions between repeat units, separated by more than three bonds along the chain or between different chains, are given by a Lennard-Jones potential:

For computational convenience, the nonbonded interaction is often truncated at rather short distance R_ij between the segments i and j.¹ Even with these simplifications, the computation of polymer properties, such as the end-to-end distance or the mean-square radius of gyration, is extremely tedious and time-consuming. This is why computations are restricted to relatively short chains.

References

1. D. Rigby and R.J. Roe, J. Chem. Phys. 87, 7285 (1987); J. Chem. Phys. 89, 5280 (1988)
2. A united-atom is a pseudo-particle that has the same molecular mechanical properties as
   the group of atoms it replaces.
3. The Hamiltonian often corresponds to the toal energy of the system (polymer chain).