Emulsion Polymerization
Smith-Ewart Theory

The first qualitative mechanism for emulsion polymerization was suggested by Harkins in 1945.^1,2 He postulated that the main locus of chain growth can be found in the stabilized polymer particles rather than in the large monomer droplets. Based on this assumption, Smith and Ewart developed a quantitative model in the late 1940th.^3,4 This model is known as the 'Smith-Ewart Model' which has been later modified and extended by various authors to include different particle formation and growth mechanisms as well as particle size distributions and particle morphologies.⁶ However, the original Smith-Ewart Theory remains very popular and has been cited in many scientific articles.

The Smith-Ewart model describes the time evolution of the number of particles containing n radicals (denoted N_n) by considering the kinetic events that lead to the capture and loss of free radicals within the polymer particles. Some of the most common kinetic events that dictate the rate of formation and growth of latex particles are shown below including radical entry, radical exit, and bimolecular termination.

Kinetic Processes of Emulsion Polymerization

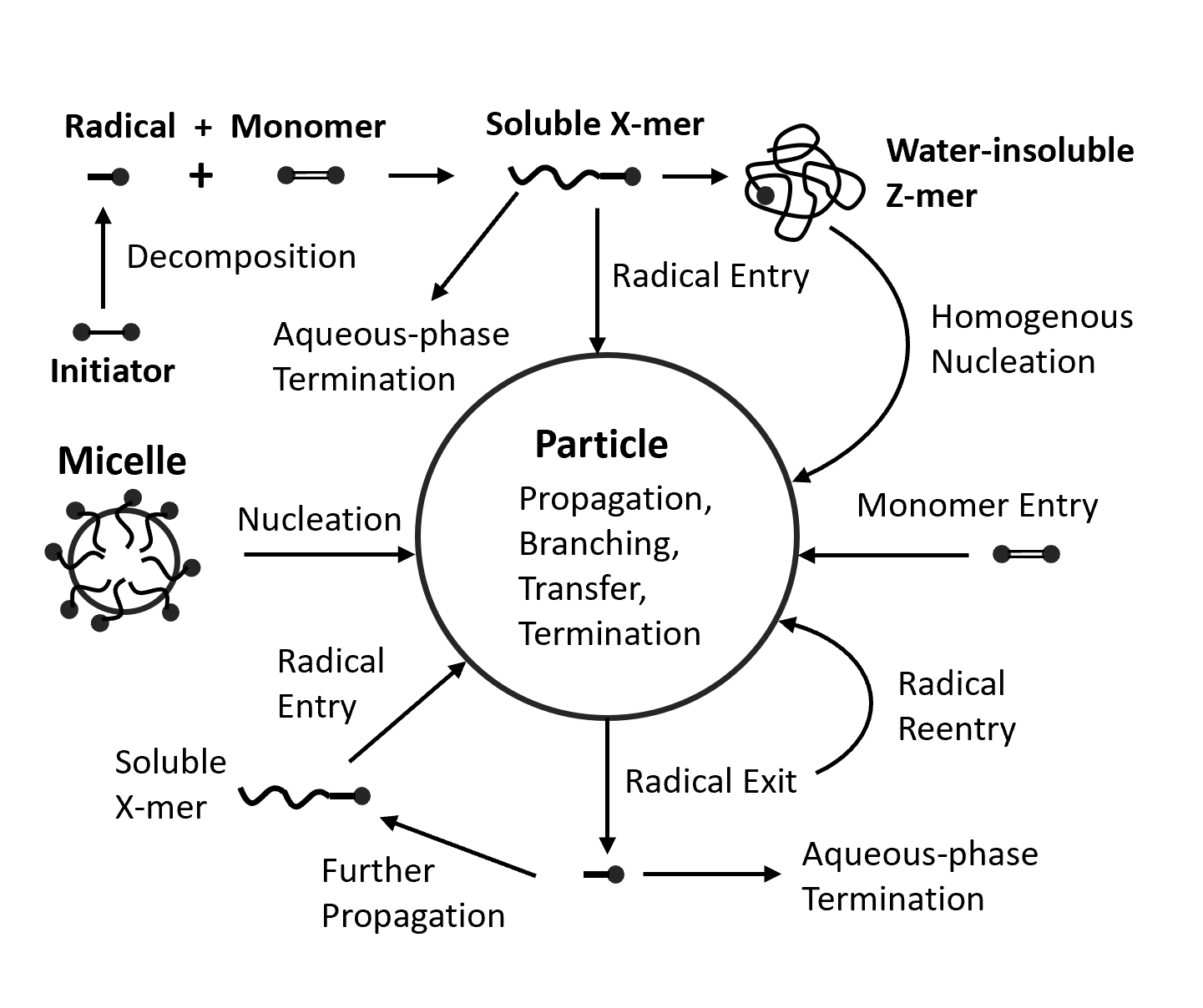
The number of radicals generated in the aqueous phase per unit volume of water and second (ρ_iw) is linear proportional to the initiator concentration [I] and thus, can be described as a first order reaction:

ρ_iw = 2 k_dw f [I]

where k_d is the rate constant for initiator decomposition, and f is the initiator efficiency. Not all of the produced radicals will initiate polymer growth because some will undergo a bimolecular termination reaction which is given by the usual expression^a

ρ_tw = - 2 k_tw [R_w·]²

where k_tw is the rate coefficient for bimolecular radical termination and [R_w·] is the radical concentration in the water phase. The rest of the radicals will eventually enter monomer swollen micelles or polymer particles. Its rate depends on the number of particles (N_T),  their radius r_p and the concentration of (oligomeric micelle soluble) radicals, [R_w,o·],:

ρ_p = k_pD [R_w,o·] N_T

where k_pD is diffusion-controlled propagation rate coefficient which can be estimated from the Smoluchowski's equation:

k_pD =  4 π D_w r_p N_A

where D_w is the diffusion coefficient of a (oligomeric) radical in the aqueous phase, r_p is the (average) radius of a particle, and N_A is the Avogardo number.¹¹
Not all of the radicals entering monomer swollen micelles will initiate polymerization, that is, some will escape from the particles. The overall rate of this process is proportional to the total number of particles (N_T), the average number of radicals per particle (n), and to the reciprocal particle size (a_p/v_p):

ρ_f = N_T n k_de a_p/v_p

where a_p and v_p are the surface area and volume of a particle. Assuming the concentration of radicals in the water phase is constant (equilibrium conditions), the overall rate of radicals entering polymer particles, ρ_p, should be equal to the sum of the rates of the three other processes:

ρ_p = ρ_iw + ρ_tw + ρ_f = 2 k_dw f [I] - 2 k_tw [R_w·]² + N_T n k_de a_p/v_p

Some of the free radicals within the particles may undergo a bimolecular homo- or heterotermination when more than one radical is present in the particles. The rate of this process is proportional to the number of possible radical combination reactions, n·(n - 1) / 2, and the number of particles N_n containing n radicals, and inverse proportional to the (average) volume of the monomer swollen particle (v_p):

ρ_tp = k_tp/2v_p · n·(n - 1) · N_n

Using the expressions for radical entry, exit and bimolecular termination and population balance, Smith and Ewart derived following recursion equation for the time evolution of the population of particles containing any number of radicals:^3,4

dN_n / dt = ρ_p/N_T · [N_n-1 - N_n] + k_de a_p/v_p · [(n + 1)·N_n+1 - n·N_n]
+ k_tp/2v_p · [(n + 2)·(n + 1)·N_n+2 - n·(n - 1)·N_n]

The population of latex particles is often normalized such that

N_T = ∑ N_n  = 1;     n = ∑ n·N_n

The Smith-Ewart recursion equation can then be rewritten as

dN_n / dt = ρ · [N_n-1 - N_n] + k · [(n + 1)·N_n+1 - n·N_n]
       + c · [(n + 2)·(n + 1)·N_n+2 - n·(n - 1)·N_n]

where c is the pseudo first-order rate coefficient for termination (k_tp/2v_p), ρ is the rate of radical entry per particle (ρ_p/N_T), and k is the rate for radical exit from a particle (k_de a_p/v_p).⁵ This recursion equation has been solved by several authors using various methods whereas Smith and Ewart presented solutions only for some limiting cases.

Case 1: ρ << k: n << 1/2

In this case, chain transfer of radicals to monomers and subsequent desorption from the particles and termination in the aqueous phase is much faster than radical absorption and propagation. Since the probability for the entry of two radicals into a particle is very small, termination reactions can be neglected. Then only one recursion equation needs to be considered:

dN₀ / dt = - ρ·N₀ + k·N₁ 

Since there are many more N₀ particles than N₁ particles it follows N₀ ≈ N_T leading to:

n = ρ /k ≈ N₁ / N_T = N₁

Two common examples of case I emulsion polymerization systems are vinyl acetate and vinyl choride.⁷

Case 2: k << ρ << c: n = 1/2

This situation leads to instantaneous termination when a second radical enters the latex particles already containing a radical. This case is also known as the zero-one limit. Radical desorption is typically negligible. Since the time interval between radical entries varies in a random fashion, both the active and inactive periods of each particle should be approximately equal in length. Thus⁸,

N₁ ≈ N₀   and   n = N₁ / N_T  ≈ 1/2

The rate of polymerization for this special situation is given by

R_p = 0.5 N_T k_p [M]_p 

It has been found that only few systems under relative few experimental situations assume the limiting value of n = 0.5.^6,7

Case 3: c << ρ: n >> 1/2

This situation is encountered when the pseudo-first-order rate coefficient for bimolecular termination, c, is very small while termination in the aqueous phase and desorption are less important. Then bimolecular termination is no longer instantaneous on entry of a second radical in an active latex particle so that the radical number is much larger than one. This situation typically occurs in large particles and/or at very low temperatures when termination reactions become diffusion controlled. If n is sufficiently large, following condition holds for steady-state conditions⁹

n²  ≈ ρ / 2c 

R_p = k_p n N_T [M]_p / N_A

For the case III, the polymerization rate is typically independent of the number of particles, N_T. This type of polymerization is very common in conventional MMA emulsion polymerization at high conversions.¹⁰

References & Notes

1. W.D. Harkins, J. Chem. Phys. 13, 381 (1945); 14, 47 (1946)

2. W. D. Harkins, J. Am. Chem. Soc., 69, 1428 (1947).

3. W.V. Smith, and R. H. Ewart, J. Chem. Phys. 16, 592 (1948)

4. W.V. Smith, J. Am. Chem. Soc. 71, 4077 (1949)

5. ρ and k are the average fraction of free radicals entering and exiting a latex particle per second.

6. Q. Wang, S. Fu, and T. Yu, Prog. Polym. Sci., Vol. 19, 703 - 753 (1994)

7. A. Penlidis J. F. MacGregor A. E. Hamielec, J. Appl. Poly. Sci., 35, 8, pp. 2023-2038 (1988)

8. If particles contain only zero or one radicals, only two recursion equations need to be considered:
       dN₀ / dt = ρ · [N₁ - N₀] + k·N₁
       dN₁ / dt = ρ · [N₀ - N₁] - k·N₁

9. K. Matyjaszewski, T.P. Davis, Handbook of Radical Polymerization, John Wiley & Sons, Inc. 2002

10. S. Sajjadi and M. Yianneskis, Polym. React. Eng., Vol. 11, Issue 4 (2003)

11. k_pD calculated with the Smoluchowsky equation represents only the upper bound because it is assumed that every collision of an aqueous monomeric radical with a latex particle results in a successful re-entry. This is why the Smoluchowsky equation usually predicts too high k_pD values.