Binary Composition Variation
of Vinyl Copolymers

Composition As A Function of Blend Conversion

Copolymerizations, in which two or more vinyl monomers react with each other to form a copolymer, have been known for almost a century. The earliest investigations and developments were directed towards the formation of rubbery copolymers of dienes, which is still one of the most important applications.

The relations that describe the composition of the feed and the copolymer as a function of feed conversion were developed by Mayo, Walling, and others in the 1940th^1-4. Below, we give a brief description of these models.

Consider a blend consisting of two monomers A and B. The Growing polymers will have either terminal A or terminal B units. Blending two monomers results in four simultaneously occuring propagation reactions with different rate equations:

A· + A → A·      R_AA = k_AA [ A·] [ A ]

A· + B → B·      R_AB = k_AB [ A·] [ B ]

B· + B → B·      R_BB = k_BB [ B·] [ B ]

B· + A → A·      R_BA = k_BA [ B·] [ A ]

where A· and B· represent chain radicals of type A and B, that is, the chains terminal, free radical bearing unit is a monomer of type A and B. It is assumed that radicals ending in A - A· and B - A· have equal reactivities towards any given monomer.
If the polymer chains are sufficiently long, both initiation and termination are exceedingly rare events.  Furthermore, at a steady state, the generation and elimination of radicals are equal, and monomers are only consumed in the propagation reaction. Then we have

k_BA [ B·] [ A ] = k_AB [ A·] [ B ]

The rates of monomer consumption are given by

d[A]/dt = k_AA [ A·] [ A ] + k_BA [ B·] [ A ]

d[B]/dt = k_BB [ B·] [ B ] + k_AB [ A·] [ B ]

To eliminate the radical concentration, we divide the first equation by the second equation. We then obtain the Mayo-Lewis² equation:

d[A]/d[B] = n = ([ A ] / [ B ]) · (r_A [ A ] + [ B ]) / (r_B [ B ] + [ A ])

where r_A and r_B are monomer reactivity ratios defined by

r_A = k_AA / k_AB

r_B = k_BB / k_BA

The equation above is generally known as the copolymer composition equation. It gives an instantaneous relationship between n, the instantaneous or incremental composition of the copolymer and the monomer concentrations [ A ] and [ B ] of the feed. To predict the composition of a copolymer based on the reactivity ratios, we introduce two more variables: the mole fraction of unreacted monomer f_A and the mole fraction in an increment of copolymer F_A formed at a given stage in the polymerization process:

f_A = [A] / ([A] + [B]) = 1 - f_B

F_A = d[A] / (d[A] + d[B])

 = (r_Af_A² + f_Af_B) / (r_Af_B² + 2f_Af_B + r_Bf_B²)

By definition, r_A and r_B describe the relative preference of a certain radical to add to its own monomer in the growing polymer chain. If, for example, r_A is greater one, then the radical of type A has a preference to react with a monomer of the same kind, and if r_A is smaller one, than it is more likely that it reacts with a monomer of the other kind. 

Sometimes it is desired to calculate a mean value of n as a function of conversion. This relation can be derived by integrating the Mayo-Lewis equation. Mayo and Lewis obtained following equation:²

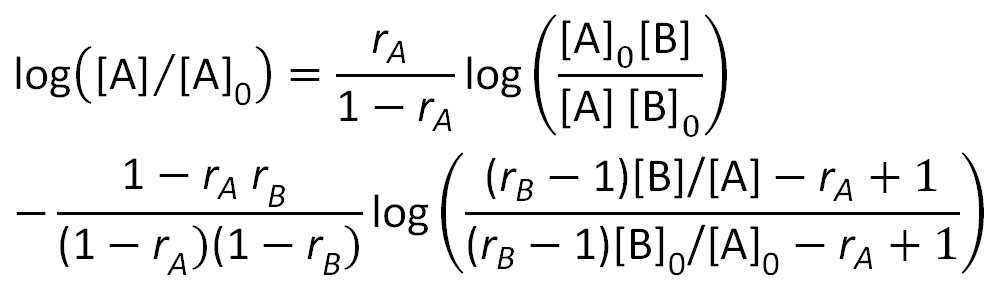
where [A]₀, [B]₀ and [A], [B] represent the initial and final monomer concentrations respectively. The equation above yields [B] as function of [A] when the initial concentrations [A]₀, [B]₀ and the relative reactivities r_A and r_B are known. In practice, one often wants to know the mean value of n for a known degree of conversion [M] / [M₀]. The equation above does not provide this information. But this relation can be easiliy derived from mass balance considerations: Let f_A = [A] / [M] and F_A = d[A] / d[M] represent the instantaneous mole fractions of monomer A in the monomer mixture and copolymer at a certain degree of conversion. Then of d[M] moles of monomer copolymerized during a given small increment of reaction, the reacted amount of A is F_A d[M]; during this increment f_A changes to f_A - df_A. Thus

f_A [M] - F_A d[M] = (f_A - df_A) [M - dM]

or

-d[M] / [M] = df_A / [F_A - f_A]

This result can be converted to the integral form:

-log [M] / [M₀] =

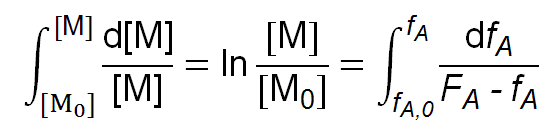
where [M₀] = [A₀] + [B₀] and f_A,0 = [A₀] / [M₀]. For given reactivity ratios r_A and r_B, F_A maybe calculated as a function of f_A (see relation above). The integral may then be evaluated graphically or numerically to obtain values for the degree of conversion 1 - [M] / [M₀]. One can obtain following closed form integral:

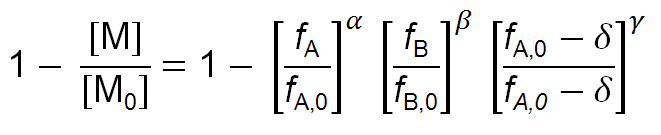
where

α = r_B / (1 - r_B)     β = r_A / (1 - r_A)

γ = (1 - r_A r_B)/ [(1 - r_A) (1 - r_B)]     δ = (1 - r_B) / (2 - r_A - r_B)

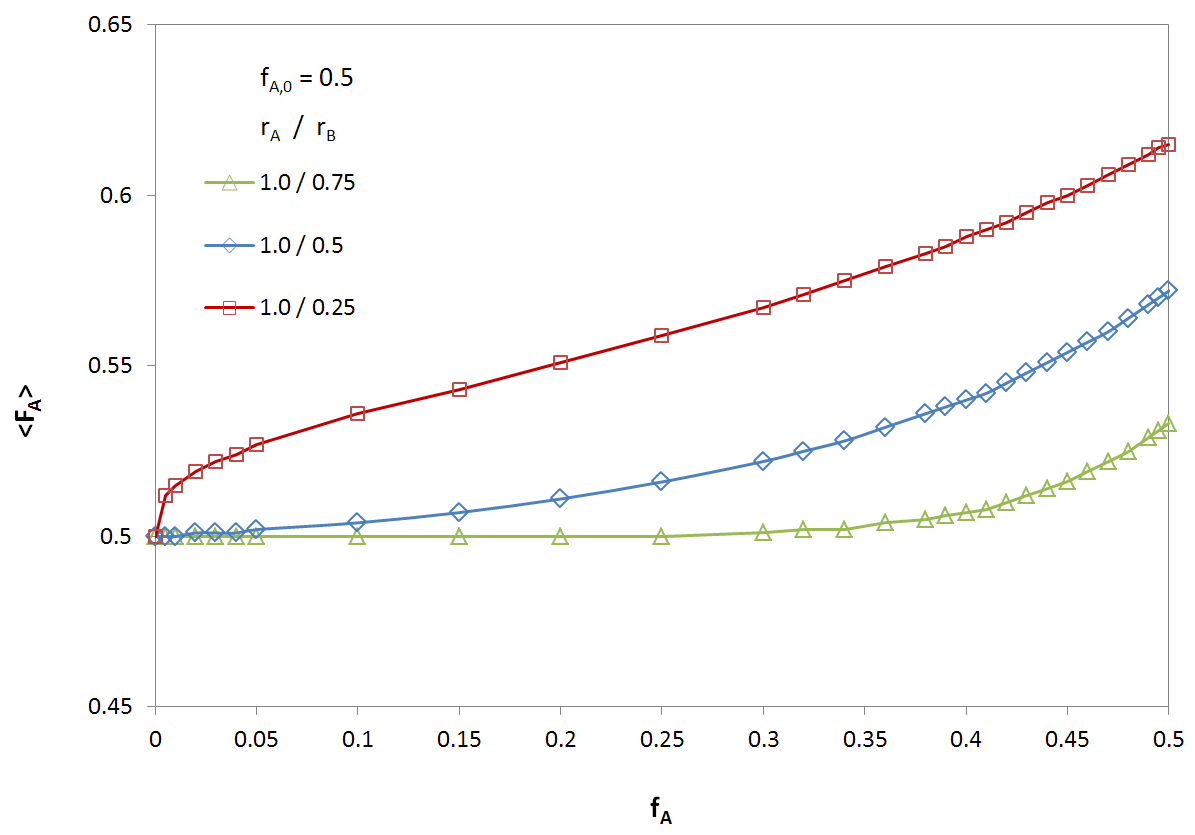
The variation of the feed composition gives the instantaneous composition of the copolymer as a function of conversion. However, it is often more useful to calculate the overall average composition <F_A> for a given conversion. This can also be done through material balance:

f_A,0 · [M₀] = <F_A> · ([M₀] - [M]) + f_A · [M]

or

<F_A> = (f_A,0 - f_A·([M] / [M₀]) / (1 - [M] / [M₀])

Another important relation is the average monomer ratio in the copolymer <n> = Δ[A] / Δ[B]. This quantitiy is obviously given by

<n> = ([A] - [A₀]) / ([M₀] - [A₀] - [M] + [A])

or

<n> = (f_A0 - f_A · [M] / [M₀]) / (1 - f_A0 - (1 - f_A) · [M] / [M₀])

The figures below shows the overall average composition <F_A> of an A-B copolymer as a function of degree of conversion 1 - [M]/[M₀] for different reactivity ratios r_A/r_B and for an initial feed composition of f_A0 = 0.5. The rate of consumption, and thus, the composition of the copolymer, strongly depend on the reactivity ratio r_A/r_B; for a large reactivity ratio, the rate of consumption of monomer A by either radicals is much greater than the rate of consumption of monomer B. Thus, for a low degree of conversion, the average composition of the A-B copolymer noticeably deviates from the initial composition of the feed, which, of course, is identical with the copolymer composition at full conversion: <F_A∞> = f_A0 = 0.5.

 

Average Copolymer Composition as a Function of degree of conversion for Different Reactivity Ratios

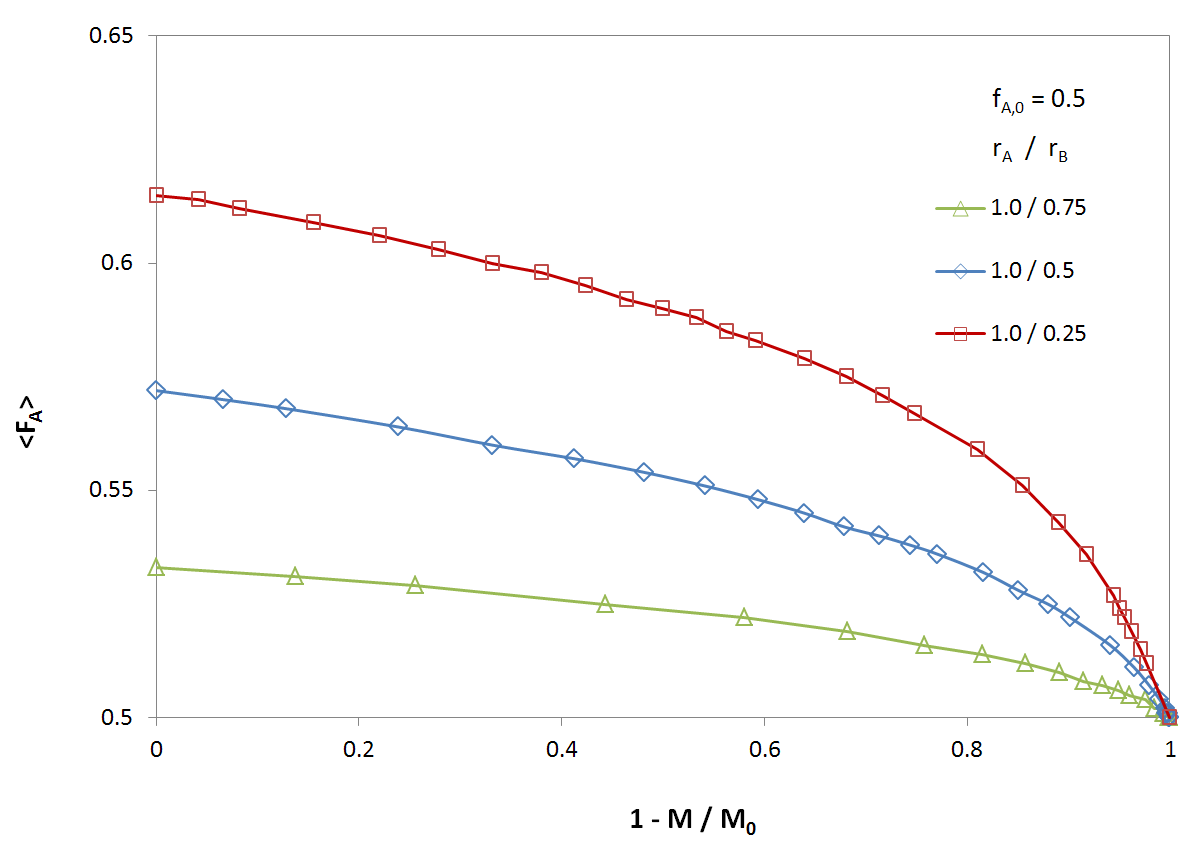
The figures below shows the overall average composition of an A-B copolymer as a function of monomer composition f_A for different reactivity ratios r_A/r_B and for an initial feed composition of f_A0 = 0.5. For large reactivity ratios, the rate of consumption of monomer A is much greater than that of monomer B; therefore; monomer A gets consumed faster than monomer B.

 

Average Copolymer Composition as a Function of Monomer Composition for Different Reactivity Ratios

References

1. C. Walling, J. Am. Chem. Soc. 71, 1930 (1949)
2. F.R. Mayo, F.M. Lewis, J. Am. Chem. Soc. 66, 1594 (1944)
3. F.T. Wall, J. Am. Chem. Soc. 66, 2050 (1944)
4. T. Alfrey, G. Goldfinger, J. Chem. Phys. 12, 205 (1944)
5. V.E. Meyer, G.G. Lowry, J. of Poly. Sci. Part A: Vol. 3, PP. 2843-2851 (1965)