Azeotropic Copolymerization

Copolymers constitute a large portion of commercial polymers. The monomers can have similar of very different physical properties, which results in a large variety of copolymers with very different properties and end uses.

The incremental composition of the copolymers (i.e. the compostion along the backbone) will usually vary, because the monomers have different reactivites; to be more specific, the composition of the copolymer will depend on the reactivity ratios:

r₁ = k₁₁ / k₁₂

r₂ = k₂₂ / k₂₁

where k_xy are the reaction constants of the four different types of polymerization reactions:

M₁^* + M₁ → M₁M₁^*      R₁₁ = k₁₁ [M₁^*] [M₁]

M₁^* + M₂ → M₂M₁^*      R₁₂ = k₁₂ [M₁^*] [M₂]

M₂^* + M₂ → M₂M₂^*      R₂₂ = k₂₂ [M₂^*] [M₂]

 M₂^* + M₁ → M₁M₂^*      R₂₁ = k₂₁ [M₂^*·] [M₁]

where M₁^* and M₂^* represent chains terminating in a unit M₁ and M₂.
Both the composition of the monomer blend f₁ and the composition of the copolymer increments F₁ (usually expressed as mole fractions) will vary throughout the polymerization. Thus, the polymer produced over the range of conversion will vary in composition along the backbone.

The figure below shows the incremental polymer composition as a function of monomer composition for different reactivity ratios. If the reactivity ratios of the two monomers are both either less or greater than unity, the curves cross the straight line f₁ = F₁. The point of interception is the so called azeotropic blend. In analogy to vapor-liquid equilibria, the composition of an azeotropic blend will be constant throughout the polymerization, that is, both the feed and the copolymer composition will not change.

Incremental Polymer Composition as a Function of Monomer Composition for Different Reactivity Ratios

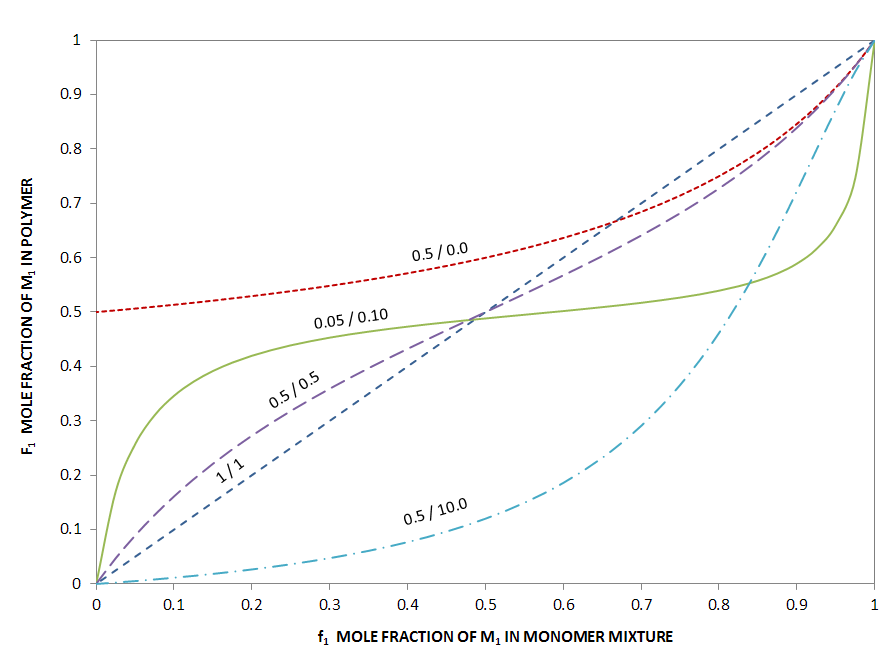
The condition for azeotropic monomer blends can be calculated with the Mayo-Lewis equation:

d[M₁]/d[M₂] = (|M₁|/|M₂|) · (r₁[M₁]/[M₂] + 1) / ([M₁]/[M₂] + r₂)

With d[M₁]/d[M₂] = (|M₁|/|M₂|) this equation reads

 [M₁] / [M₂]  = (1 - r₂) / (1 - r₁)

f_1,c = (1 - r₂) / (2 - r₁ - r₂ )

If both reactivity ratios are smaller or greater than unity, then f_1,c has non-negative solution and an azeotropic blend exist. However, if  r₁ > 1 and  r₂ < 1 or r₁ < 1 and  r₂ > 1, then no critical blend exist.