Transmission, Reflection, and Absorption Behavior of Polymers

The optical properties of polymers, including haze, gloss, and transparency, are critical to many applications of commerical plastics. The transmittance of a material is defined as the ratio of light intensity passing through the material to the intensity of light received by the specimen. It is determined by reflection, absorption and scattering. If both absorption and scattering are negligible, the material is called transparent. In contrast, an opaque material has practically zero transmittance due to its high scattering power whereas a materials with negligible absorption but with appreciable transmittance but lower than 90% is called translucent.

Gloss is an optical property which describes how well a surface reflects light in specular direction. It is of great practical importance for many applications. The reflectivity (or reflectance) is defined as the fraction of incident light intensity reflected at the interface (surface effect). Only highly polished metal mirrors have nearly total reflectance. If the reflectance is almost zero, the surface appears totally matt. A material with reflectance in between these two extremes is called glossy or shiny. The gloss is responsible for the lustrous appearance of plastic films.

The fraction of the light intensity that neither enters the material nor follows the pass of mirror reflection is dispersed or scattered by diffraction. The lustrous appearance of a plastic is determined by both the reflection and diffraction, meaning the shininess of a surface depends on both the specular reflection and the diffuse light of the surrounding surface area, which is often called the contrast gloss or luster.

 

 

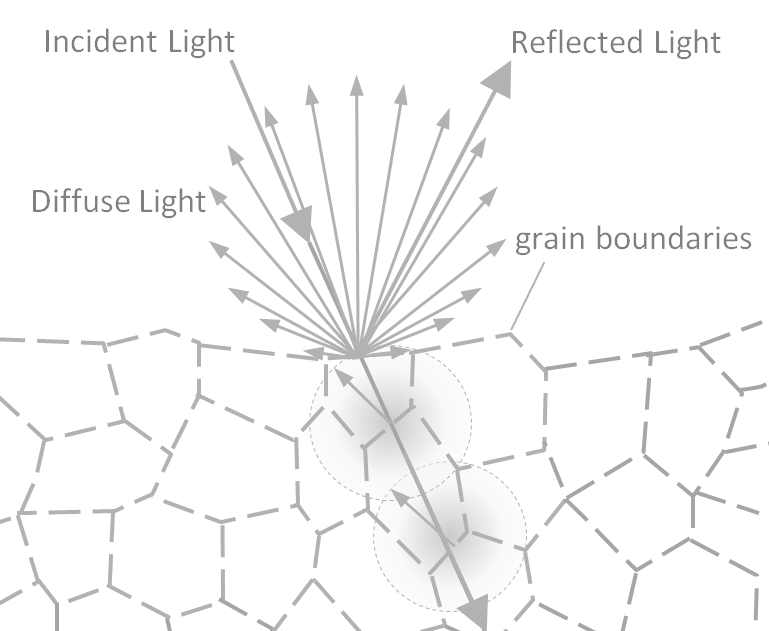
The root cause of opacity in polymers is light scattering and absorption. The more light is scattered or absorbed the more the material becomes opaque. Light scattering is a purely physical phenomenon: light hitting insulating matter induces dipole oscillations in the material. Each induced dipole then acts as a secondary source of light and emits photons in all directions, the so called scattered light. This, in turn, reduces the intensity of directly transmitted light. Pure light scattering will not cause any loss of radiation energy. However in the case of colored or filled plastic, a portion of the light is absorbed by the material, that is, radiation energy is transformed into other forms of energy like induced molecule motion (thermal energy). Assuming a linear absorption mechanism the decrease in radiation intensity as a function of penetration depth can be described by the Lambert absorption rule

I_T (z) = I₀ · exp (- α_A · z)

where z is the penetration depth of the light and α_A = 4 π κ / λ is the wave length dependent absorption constant. The Lambert absorption rule states that within every differential layer of material, dz, the same fraction of radiation is absorbed which leads to an exponential decrease of transmitted radiation.
Light scattering in clear polymers is caused by optical inhomogeneity such as phase boundaries, pores and inclusions, to be more specific, light scattering in clear plastics arises from fluctuations in refractive index due to fluctuations in composition and/or packing density (volume effect) whereas a defect-free crystalline solid provides no scattering centers for incoming lightwaves. However, polymers crystalls have usually many defects like phase boundaries between crystals and amorphous regions. The intensity loss due to scattering caused by inhomogeneous structures in the material can also be described with the exponential rule of Lambert. In polymeric materials, scattering of radiation like NIR and IR can be caused by the macromolecules themselves, by crystalline-amorphous phase boundaries as well as by filler particles, fibers and pigments. The type of scattering depends on the ratio of wave length λ to the size of scattering structure s. Following cases exist

I. s » λ : Diffraction on microscopic structures,
II. s ≥ λ: Mie scattering on small scattering structures,
III. s « λ: Rayleigh and Raman scattering.

In the case of diffraction on micrsocopic structures like phase boundaries, scattering is independent of the wave length. This type of diffraction often dominates in thin colorless plastic films.

The drop in radiation intensity caused by the overall scattering can by described by the exponential rule of Lambert:

I_T (z) = I₀ · exp (- α_S · z)

where α_S is the scattering coefficient of the medium. For spherical scattering structures smaller than the wavelength (Rayleigh scattering), the scattering constant is proportional to the number N and the volume V of the scattering structures as well as the wavelength of the radiation λ,

α_S = N · V / λ⁴

In the case of large spherical scattering structures (diffraction on microscopic structures), the scattering constant is proportional to the sum of the cross-sectional areas of the scattering elements:

α_S ∝ π ∑_i ρ_i²

The relationship above are only valid for spherical scattering structures like aerogels. For crystalline polymers, the mathematical description of the scattering constants is considerably more complex.

Despite many defects, thin plastic films sometimes appear perfectly clear. The explanation is simple; only when the heterogeneities are in the range of visible light, significant reflection, refraction, and scattering can be expected and the polymer film loses clarity. If, however, these regions are smaller than the wavelength of the light, the polymer appears clear.

The size and degree of crystallinity depends on many factors such as polymerization and heat-treatment conditions, composition,  structure and size of the polymer chains including polydispersity and chain branching. The clarity or transmittance of a polymer usually increases with decreasing crystallinity, refractive index, compressibility and intermolecular interaction (cohesive energy density).

The degree of scattering also depends on the surface morphology. Often a large portion of the incident light is scattered at the polymer surface as it is the case for polymer films. Scattering is caused by surface irregularities (roughness) and imperfections such as scratches (surface deffects). Surface roughness is often the most important factor. For example, it has been shown that HDPE lamellae can form large rodlike superstructures which produce rough surfaces. These surface irregularities can scatter a large portion of the incident light and cause haziness whereas polymers with less oriented lamellar structures have reduced surface roughness (smaller domains) and thus are less hazy.¹

For a perfectly smooth surface the specular reflectance, R_s = I_R / I₀, for unpolarized light of intensity I₀ can be calculated with the Fresnel equation:

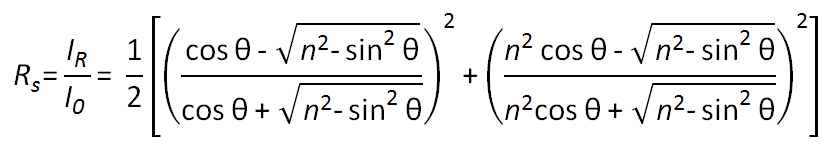
where n is the refractive index of the surface and θ is the angle of incidence. Due to surface irregularities and other imperfections, a rough surface will scatter some light in non-specular directions. This reduces the measured gloss. At a given angle θ and wavelength λ , there will be a transition from smooth to rough surface. As has been shown by Bennett and Porteus (1961) the effect of surface roughness on the reflectance can be described by the equation

R_r = R_s · exp{- [(4nσ / λ) cos θ]²}

where R_r is the specular reflectance of the rough surface and σ is the root mean square surface roughness in the units of wave length of the light.

References

1. A. Bafna, G. Beaucage et al., J. Poly. Sci.: Part B: Polymer Physics, Vol. 39, 2923–2936 (2001)
2. H. E. Bennett and J. O. Porteus, Journal of the Optical Society of America, Vol. 51, Issue 2, pp. 123-129 (1961)