Monomer Partitioning in Emulsions
(Swelling of latex Particles with Solvent)
The thermodynamic partitioning of solvent (monomer) between polymer particles and a continuous phase has long been a subject of great interest because it plays an important role in understanding emulsion systems such as emulsion-based coatings, adhesives, pharmaceuticals and healthcare products. It also plays a very important role in emulsion polymerization processes, because the monomer partitioning affects the yield, rate of polymerization, copolymer composition, and final molecular weight of the polymer.
The theory of thermodynamic partitioning of monomers in emulsions was first developed by Morton et al.3 and Vanzo et al.4. Since these early publications, the theory of partitioning has been refined and extended to account for monomer and solvent blends, and crosslinked polymer particles.5-7
Monomer Swollen Polymer Latex
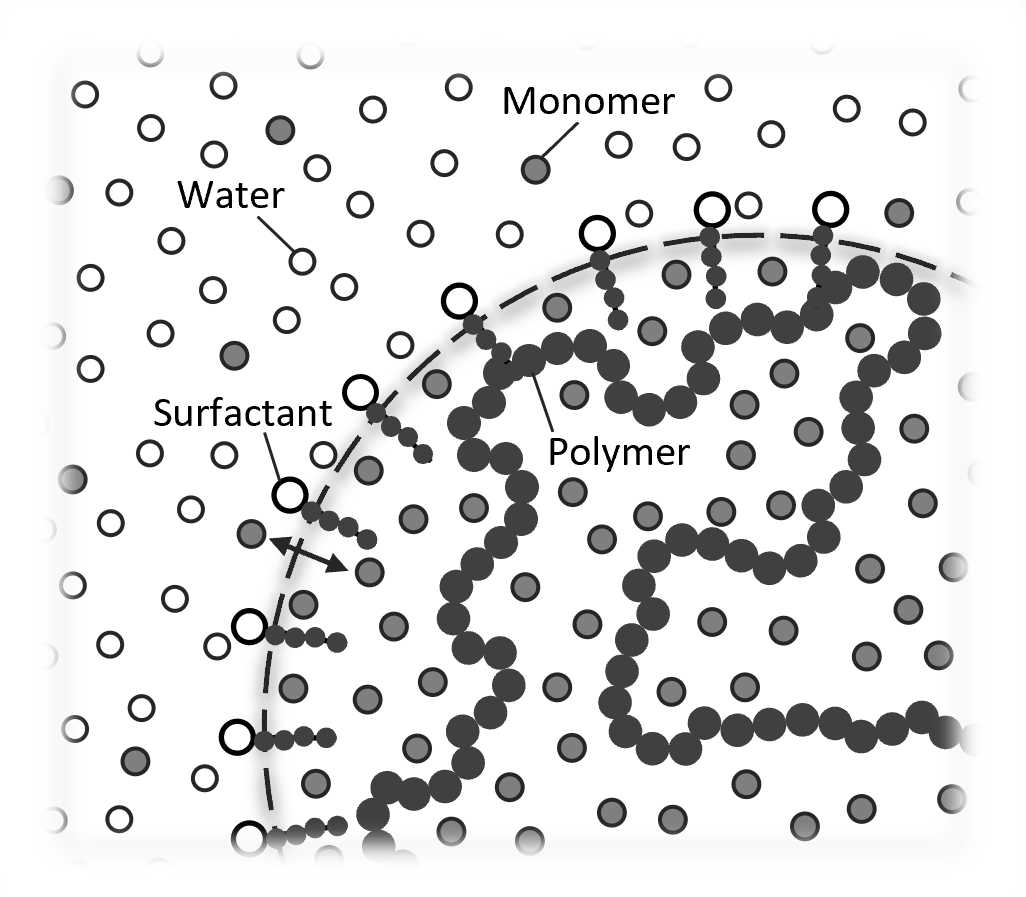
Monomer Swollen Polymer Latex
The model of Morton decribes the saturation swelling of latex particles by solvent (monomer) which has only limited solubility in the continuous phase (water), that is, the monomer in the swollen latex particles is in equilibrium with the monomer phase (droplets).3 In this situation, the partial molar Gibbs free energy (or chemical potential) of the monomer will have the same value in each of the three phases, that is, in the monomer-swollen latex particles, the monomer droplets and the aqueous phase:
Δμp = Δμm = Δμw
where Δμp, Δμm and Δμw are the chemical potential of the monomer in the latex particles, monomer droplets and the aqueous phase, respectively.9 Morton assumed that the partial molar Gibbs free energy of monomers in large particles, Δμp, can be calculated with the Flory-Huggins theory:1,2,10
Δμp,mix/RT ≈ ln [1- φp] + φp (1 - 1/Mn) + χpmφp2
where φp is the polymer volume fraction in the latex particles, χpm the Flory-Huggins interaction parameter, and Mn the number-average degree of polymerization. This equation is only correct for large polymer particles because it neglects the change of interfacial free energy when monomers enter and swell the polymer particles. For small latex particles of nanometer size this energy can not be neglected (microemulsions). Morton et al. assumed that the change of the partial molar interfacial free energy when monmers enter the polymer particles can be calculated with the Gibbs-Thomson equation:6,7,11
Δμp,int/RT ≈ 2Vm · γp φp1/3 / Rp,0
where where Vm is the partial molar volume of the monomer, γP is the particle-water interfacial tension, and Rp,0 is the unswollen radius of the latex particles.
When the swollen latex particles are in equilibrium with the free monomer phase the partial molar free energy of the monomer is zero:
Δμp = Δμp,mix + Δμp,int = 0
Combining both equations above gives the so-called Morton equation:
Δμp / RT = ln [1- φp] + φp · (1 - 1/Mn) + χpmφp2 + 2Vm · γp φp1/3 / Rp,0 = 0
The molecular weight is normally large, then this equation may be written in a simpler form
Δμp / RT = ln [1- φp] + φp + χpmφp2 + 2Vm · γp φp1/3 / Rp,0
Morton's equation is only applicable to saturated solutions, or in other words, to with monomer saturated latex particles. The partial swelling of latex particles by monomer was first considered by Vanzo. Vanzo assumed that the partial molar Gibbs energy of the monomer in the aqueous phase can be calculated with Henrys law:4,5
Δμw / RT = ln ([M]w/[M]w,sat)
At equilibrium, the partial molar Gibbs free energy of the monomer in the latex particles and in the continuous phase will be equal:
Δμp = Δμw
or
ln ([M]w/[M]w,sat) = ln [1- φp] + φp + χpmφp2 + 2Vm · γp φp1/3 / Rp,0
Vanzo's equations does not account for crosslinks in the polymer. A three-dimensional network polymer when absorbing large amounts of monomer will experience an elastic deformation like a rubber band. Thus, an elastic retractive force develops. This force and the resulting change in free energy can be calculated with the Flory-Rehner theory:8
Δμp,elas= (Vm ρp / Mc) · [φp1/3 - φp/2]
Combining this equation with the Vanzo equation gives:6,7
ln
([M]w/[M]w,sat)
= ln [1- φp] +
φp + χpm φp2 +
2Vm · γp φp1/3 / Rp,0
+ (Vm ρp / Mc) · [φp1/3 - φp/2]
Methyl Acrylate Partitioning for PSMA Latex in Water
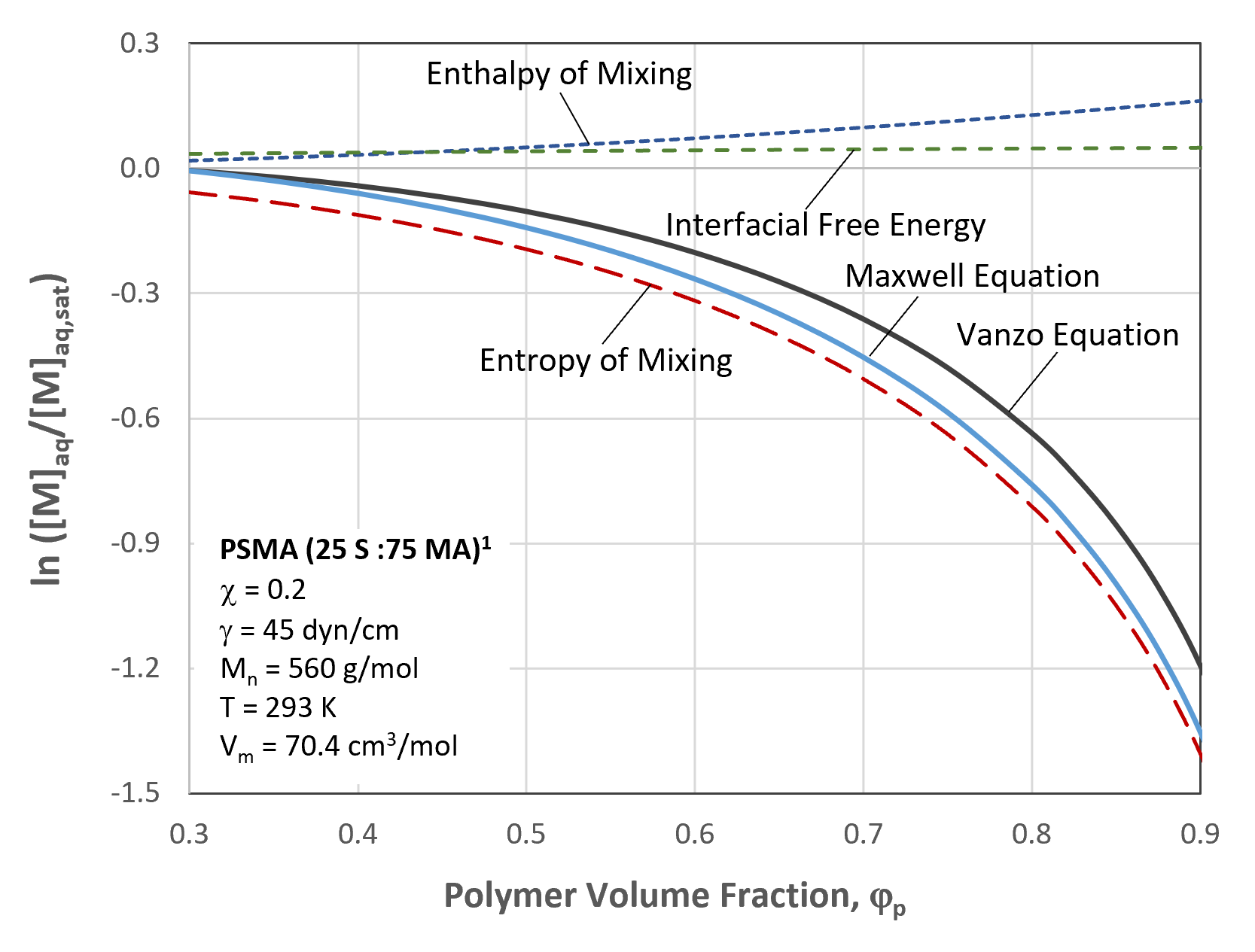
The figure above shows the contributions of the different terms of the Vanzo equation to the partitioning of methyl acrylate (MA) monomer between the aqueous phase and in water dispersed styrene-methyl acrylate copolymer latex particles (R0 = 50nm). The most important term is the entropy of mixing whereas the residual energy of mixing (the χ-term) and the interfacial free energy have only a small effect on the thermodynamic partitioning at higher volume fraction of polymer. This finding has several important consequences; since the entropy of mixing depends only on the volume fraction of polymer in the latex particles, most of the other variables have little or no effect on the monomer partioning. This includes latex particle radius, temperature, polymer crosslinking density, polymer molecular weight, polymer type and polymer composition. This finding is in good agreement with the experimental measurements.6,7
The calculation of the monomer partitioning between the continuous and latex particle phases requires that both the polymer-monomer interaction parameter and the interfacial tension are known. However, these parameters have been reported for only a few systems. The situation becomes even more complicated when both these parameters depend on the polymer volume fraction, as is the case for many systems. With these complications in mind, Maxwell et al. derived following a semi-empirical equation:6
ln ([M]w/[M]w,sat) = ln [1- φp] + φp + C
where C is a correction term:
C = ln [1- φp,sat] + φp,sat + C
and φp,sat is the saturation volume fraction of polymer in the latex particles which can be calculated from the Morton equation. Thus only two parameters are needed to predict the partial monomer partitioning between the latex particle and aqueous phases, which are the saturation concentration of monomer in the aqueous phase and the monomer volume fraction in the polymer particles.
References and Notes
- P.J. Flory, J. Chem. Phys. 9, 660 (1941); 10, 51 (1942);
- M. L. Huggins, J. Phys. Chem. 46, 151 (1942); J. Am. Chem. Soc. 64, 1712 (1942)
- M. Morton, S. Kaizerman, M.W. Altier, J Colloid Sci., 9, 300 (1954)
- E. Vanzo, R.H. Marchessault, V. Stannett, J Colloid Sci, 20, 62 (1965)
- J.L. Gardon, J. Polym. Sci., Polym. Chem. Ed. 6, 2859 (1968)
- I.A. Maxwell, J. Kurja, G.H. Doremaele & A.L. German, Makromol. Chem. 193, 2049 (1992)
- A.M. Aerdts, M.M.W.A. Boei & A.L. German, Polymer 34, 3, 574 (1993)
- P.J. Flory and J. Rehner, J. Chem. Phys. 11, 521 (1943)
μp is the partial molar Gibbs free energy (or chemical potential) of monomer in the polymer phase relative to the partial molar Gibbs free energy of pure monomer.
-
The Flory-Huggins theory is a good approximation if the polymer concentrations within the latex particles is high, because a relative uniform density of Flory-Huggins segments can be expected.
The interfacial free energy of a droplet of liquid in a continuous phase reads ≈ 2Vm · γp / R (Kelvin equation). The radius of a swolling polymer coil, Rp,s, can be expressed in terms of polymer concentration in the swollen polymer coil φP ≈ Rp,03/ Rp,s3. Then Rp,s ≈ Rp,0 / φP1/3