Microemulsion Polymerization

Microemulsions are thermodynamically stable emulsions consisting of two immiscible liquids such as oil and water stabilized by a surfactant and cosurfactant.¹ The microemulsions have a heterogeneous nanostructure but these structures are smaller than the wave length of visible light and therefore,  appear homogenous at a macroscopic level. Their transparency makes them extremely attractive to many industries.

Microemulsions differ in several ways from regular emulsions; for example, they possess a much larger oil-water interface area due to the large amount of surfactant added, are optical transparent and thermodynamically stable whereas normal emulsions are opaque (milky), unstable, and have a broad particle size distribution. Microemulsion also consist of much smaller phase domains on the scale of nanometers which assume a large variety of structures depending on the concentration of oil, water and surfactant (see below).

 

Schematic Ternary Phase Diagram of
Water-Oil-Surfactant Mixtures

 

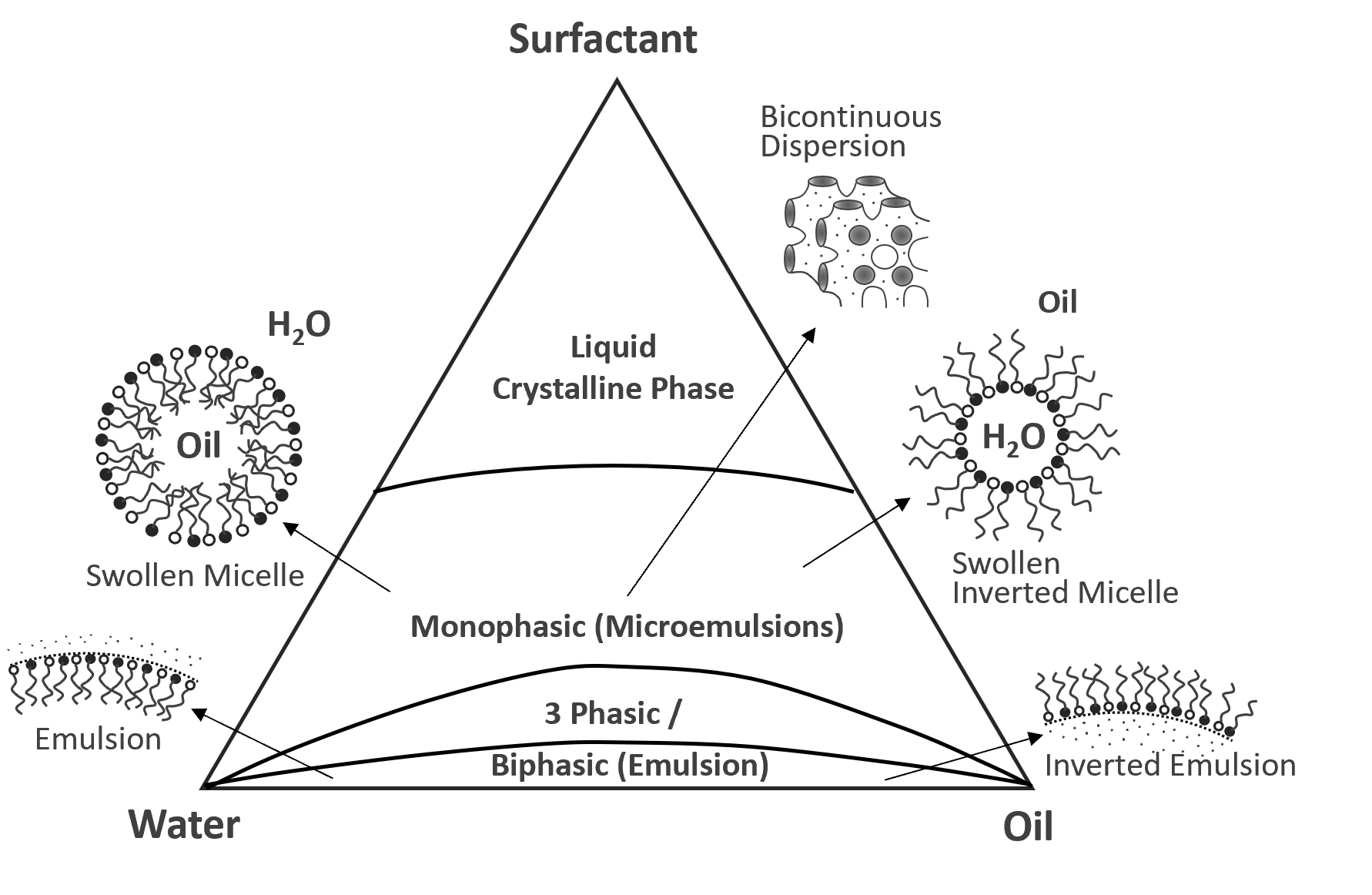
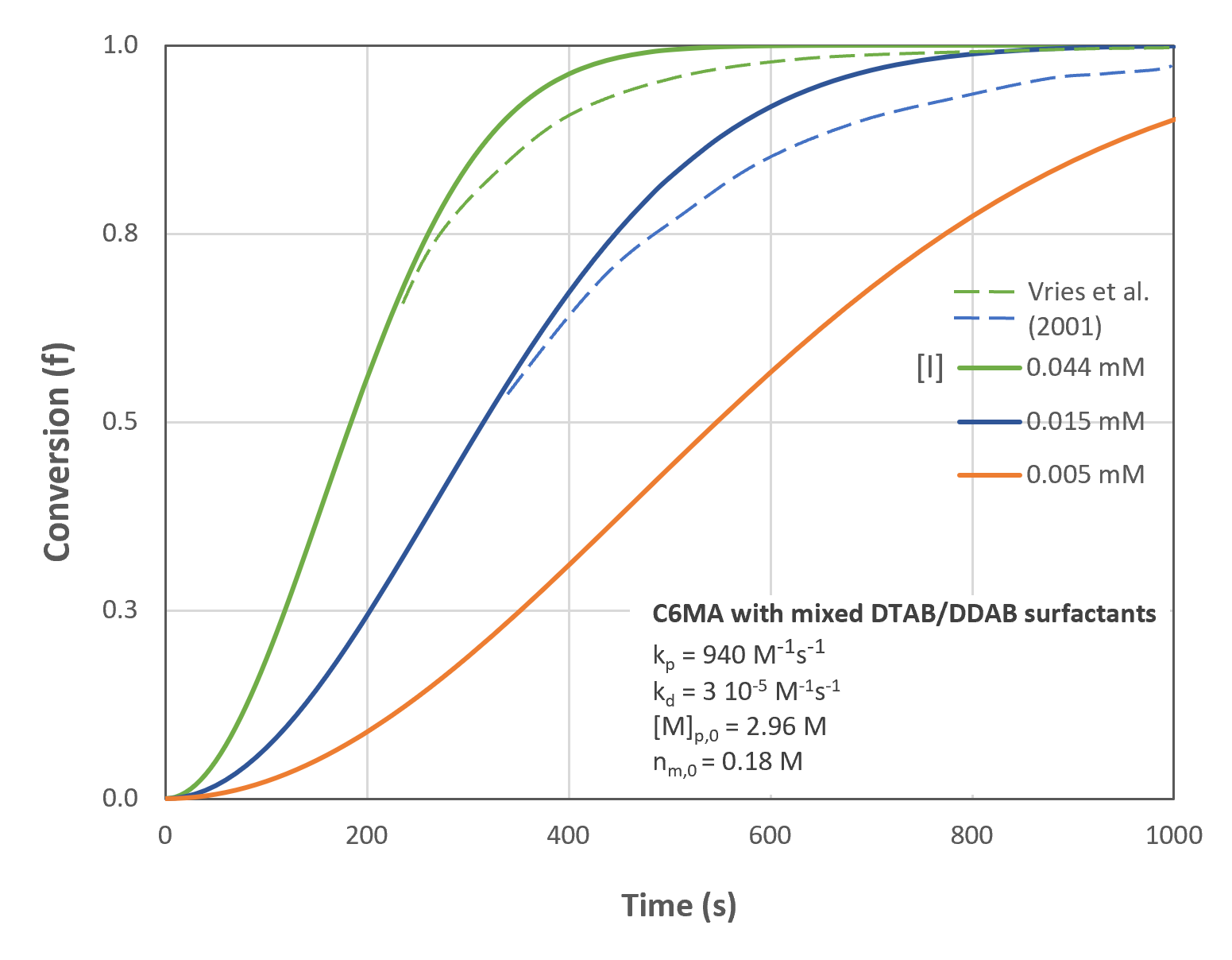
Polymerization in microemulsions was first attempted around 1980 probably inspired by the large number of studies performed on microemulsions after the 1974 oil crisis.² However, only a few attempts were made to model the reaction kinetics, and the molecular weight and particle size distributions of microemulsion polymerization. A relatively simple but very intriguing model was developed by Kaler et al.^4,5 Kaler's group was able to predict the polymerization kinetics of methacrylic monomer (C6MA) stabilized with a mixture of the surfactants didodecyldimethylammonium bromide (DDAB) and dodecyltrimethylammonium bromide (DTAB). Both the calculated particle size and molecular weight distributions are in excellent agreement with the experimental results from small-angle neutron scattering (SANS) measurements.⁵

The polymerization of hydrophobic monomers in o/w microemulsions is started by the addition of water-soluble initiators that decompose when exposed to heat. The number of radicals generated in the aqueous phase per unit volume of water and second (ρ_i,w) is assumed to be linear proportional to the initiator concentration [I] and thus, can be described as a first order reaction:^4,5

ρ_i,w = 2 k_d λ [I]

where k_d is the rate constant for initiator decomposition, and λ is the initiator efficiency (λ ≈ 1).  The reaction of a primary free radical (I·) with a monomer (M) occurs very rapidly.⁵ The growth active species (IM·) either may be hydrophobic enough to directly enter a monomer-swollen micelle to start propagating or they may require further propagation steps in the aqueous phase to become hydrophobic enough to be soluble in monomer swollen micelles.⁶ In either case, the system will typically reach a pseudo-steady-state after a short time. In other words, the rate of radicals entering (monomer swollen) micelles will equal the rate of radicals generated. The rate equation for the concentration of growing particles, N_p, can then be written as

dN_p/dt = ρ_i,w = const. ⇒ N_p = ρ_i,w · t

Kaler et al. assumed that aqueous phase propagation is negligible. This, for example, is the case for vinyl monomers with long alkyl side chains such as hexyl methacrylate (C6MA) which is (nearly) insoluble in water. They further assumed that bimolecular termination in the particles is negligible. This is the case if the concentration of growing particles, N_p, is small compared to the total number density of dead polymer particles and monomer swollen micelles, N: N_p/N << 1, i.e. the entry of two radicals into a particle is a rare event.

The fundamental rate equation for the conversion of monomers in growing polymer particles is given by

df/dt = k_p [M]_p N_p / n_M,0

where n_M,0 is the initial number of moles of monomer per unit volume of continuous phase, [M]_p is the monomer concentration in the growing polymer particles and k_p is the rate constant for propagation. Kaler et al. assumed that k_p is approximately constant over the extent of polymerisation. However, this is only the case if the polymer does not passs through its glass transition temperature during chain growth, in which case the reaction becomes limited by diffusion rather than reaction.

The concentration of monomer in the growing particles, [M], depends on the monomer partition between the polymer particles and the large number of coexisting (monomer swollen) surfactant micelles. Kaler et al. assumed that the monomer partitioning decreases linearly with monomer conversion, f, according to:^4,5

[M]_p = [M]_p,0 · (1 -  f)

If termination reactions can be neglected, the total number of growing particles is not affected by chain transfer. Combining the equations above, yields following expression for the total rate of conversion:

df/dt = A · (1- f) · t

A = k_p [M]_p,0 ρ_i,w / n_M,0

Integration gives

f(t) = 1 - exp(-½·A·t²)

This rate equation has its maximum rate at t = A^-1/2and f = 1 - e^-1/2 = 0.39.

The figures below show the conversion and rate of conversion as a function of time/conversion and initiator concentration for C6MA/DTAB/DDAB microemulsions having an initial monomer concentration in the continuous phase n_M,0 = 0.18 M and in the droplets [M]_p,0 = 2.96 M. The predictions are in good agreement with Kaler's experimental data (see SANS measurements in [5]). Only for large conversions, noticeable deviations from the measured data were observed.^5,7 Kaler et al. assumed that these discrepancies are caused by nonlinear monomer partitioning. They measured the monomer partitioning and correlated the data to the conversion by following empirical interpolation formula:

[M]_p = [M]_p,0 · (1 -  f)^b

Kinetics of Microemulsion Polymerization

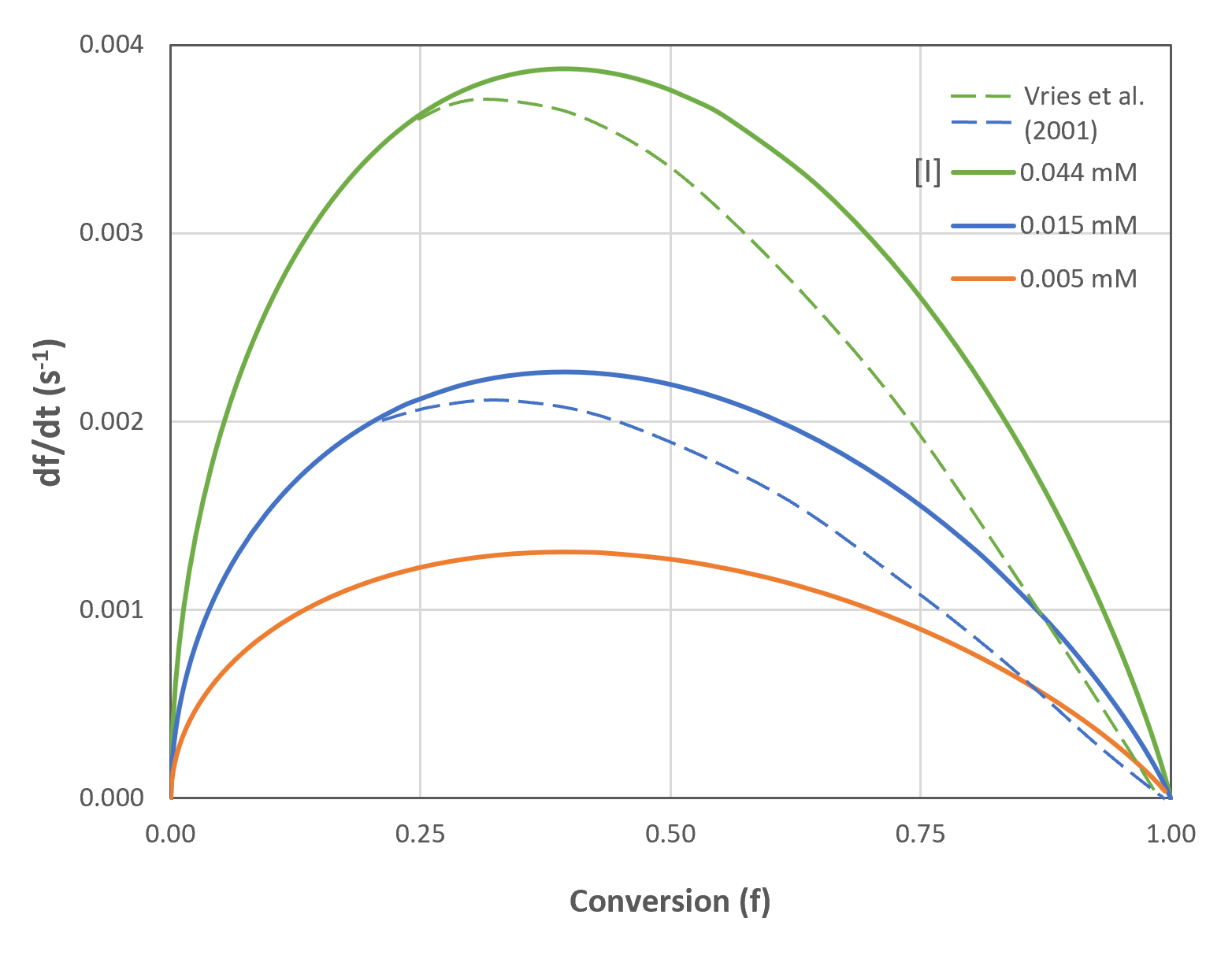
Kaler et al. originally postulated that termination of free radicals in the aqueous phase can be neglected. However, this assumption is not necessarily true for all monomers, particularly for those that have a much higher solubility in the aqueous phase while their propagation rate in the aqueous phase is noticeably smaller. Both increases the concentration of monomer-based free radicals in the aqueous phase, and thus, increases the rate of termination. To improve the accuracy of their predictions, Kaler et al. expanded their original kinetic model by including nonlinear monomer partitioning, bimolecular termination reactions and diffusion limitations to propagation.⁵

References & Notes

1. A cosurfactant is mostly added to reduce the electrostatic repulsion between adjacent surfactant molecules in the interfacial film. Thus, it is not a necessary ingredient in the formation of microemulsions.

2. F.M. Pavel, J. Dispers. Sci. Technol., Vol. 25, No. 1, pp. 1-16 (2004)

3. L. Nie, W. Yang, H. Zhangand S. Fu, Polymer 46 , 3175-3184 (2005)

4. J.D. Morgan, K.M. Lusvardi, E.W. Kaler, Macromolecules, 30, 1897-1905 (1997)

5. R. de Vries, C.C. Co, and E.W. Kaler, Macromolecules, 34, 3233-3244 (2001)

6. Kaler's model is only applicable when aqueous phase termination can be neglected. This requires initiators that undergo no or only a few aqueous phase propagation steps before becoming oil-soluble. Otherwise, the free radical concentration may build up to a level where termination in the aqueous phase is no longer negligible.

7. The dashed lines are the conversions and conversion rates predcicted with Kaler's modified model (b = 1.4).⁵