Ion Association in Anionic Polymerization
(Fuoss-Winstein Ion Pairs)

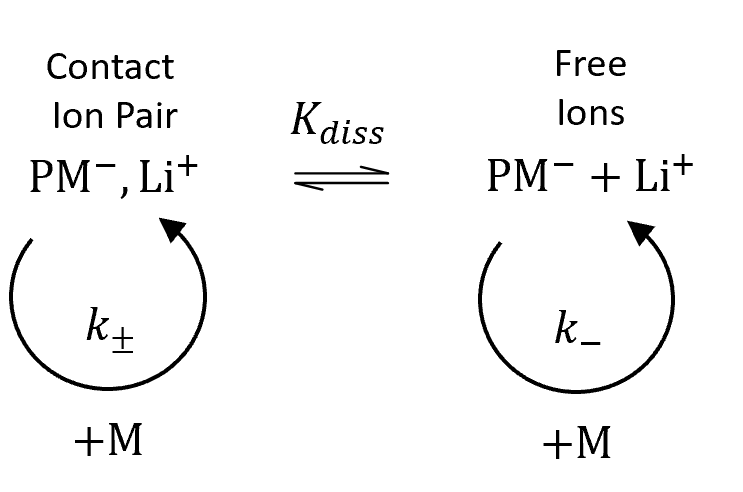
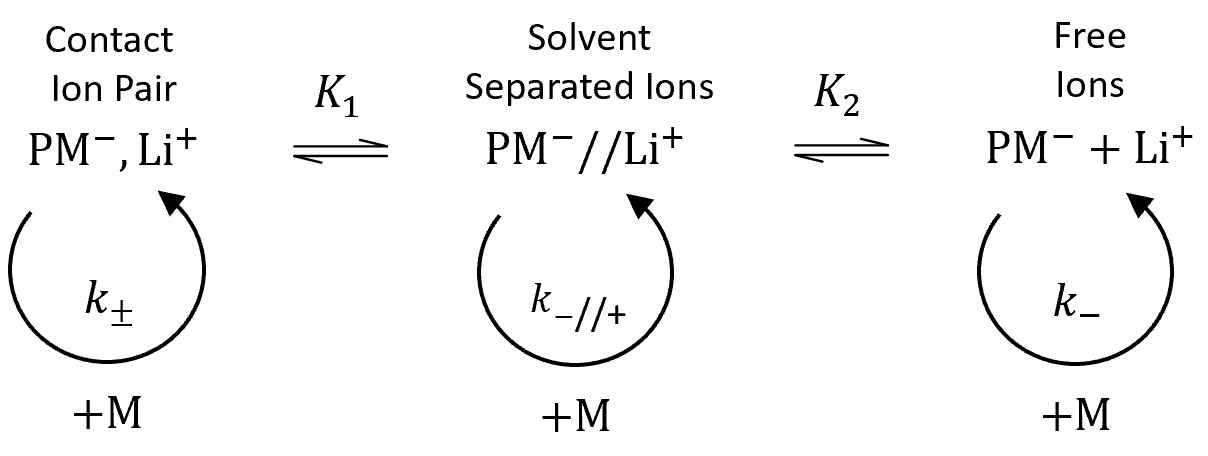
The rate of anionic polymerization of vinyl monomers strongly depends on the extend and type of active ion pairs formed during polymerization which, in turn, depend on the nature of of the reaction medium ("solvent") and ions.  According to Fuoss and Winstein et al.,^1,2 anions may associate in two different ways: they may either be tightly associated with the cations or they may be loosely associated with solvated counterions. Winstein et al. named these two types of ion pairs contact ion pairs (CIP) and solvent-separated ion pairs (SIP). Marcus et al.^3,4 suggested a third kind of solvated ion pairs where ions share one or more solvent molecules, the so-called solvent-bridged or solvent-shared ion pairs (SSIP). These three types of ion pairs are in equilibrium with each other and with free ions as shown schematically in the figure below.

 

Fuoss-Winstein Ion Pairs in Solvent

 

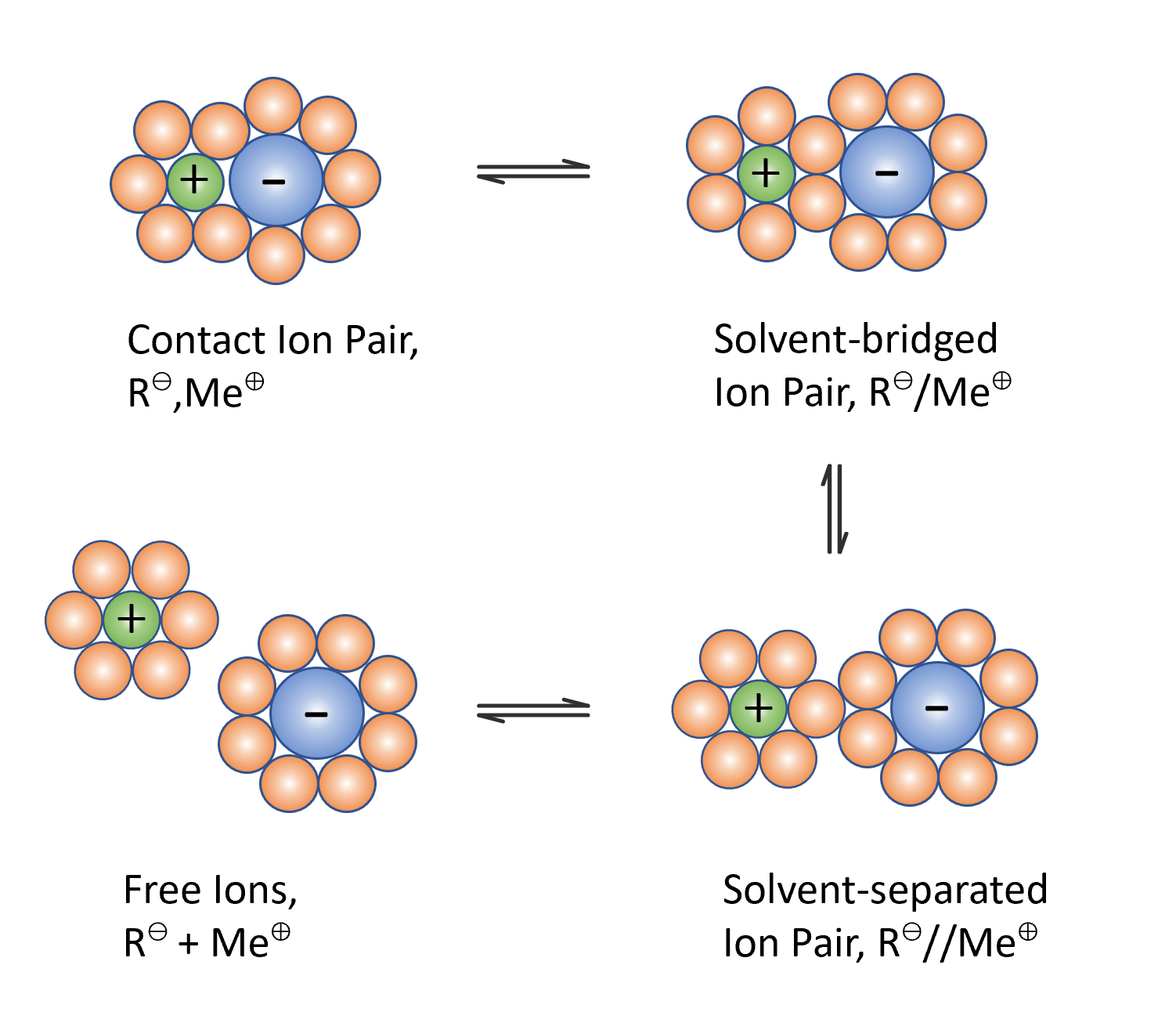
The different states of solvation and aggregation of carbanions in polar and nonpolar solvents will affect the polymerization kinetics. Often one of the three ion pairs will dominate the polymerization. Which type of ion pairs is most abundant, will depend on the type of carbanion and gegenion and on the reaction medium used in the anionic polymerization. Below, the mechanism and the kinetics of the three most common types of anionic polymerization will be briefly presented.

Model 1: Nonpolar Monomers in Nonpolar Solvents

The general mechanism of anionic polymerization is rather complicated due to the many different types of ion pairs and aggregates that can form during initiation and that can act as propagating centers. Luckily, in many cases, the contribution of one type of ion pair to the rate of polymerization dominates over those of all others. This is, for example, the case when styrene is anionically polymerized in a nonpolar solvent such as benzene using n-butyl lithium as initiator.

The kinetics of this type of polymerization was first studied by Worsfold and Bywater in 1960.⁵ They and others found that the reaction order with respect to the propagating anion depends on the solvent and initiator and is about 0.5 in benzene, toluene, and cyclohexane.^5,6 It was postulated that the polystyryllithium anions exist as less reactive dimers in equilibrium with reactive contact ion pairs in hydrocarbon solvents:

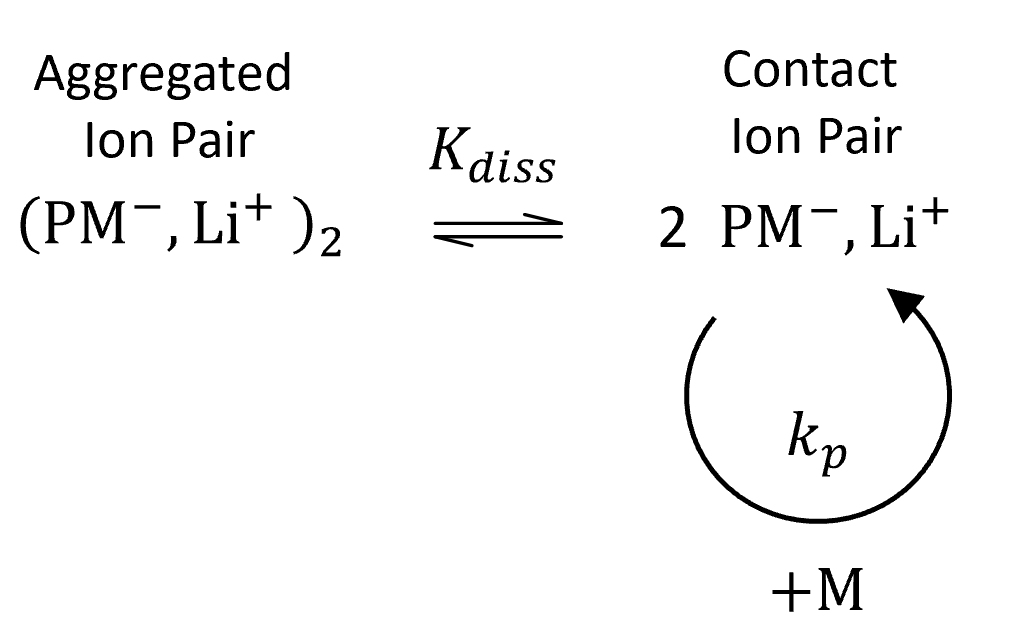
Assuming that the contribution of the dimers to chain growth is negligible, the rate of polymerization is given by

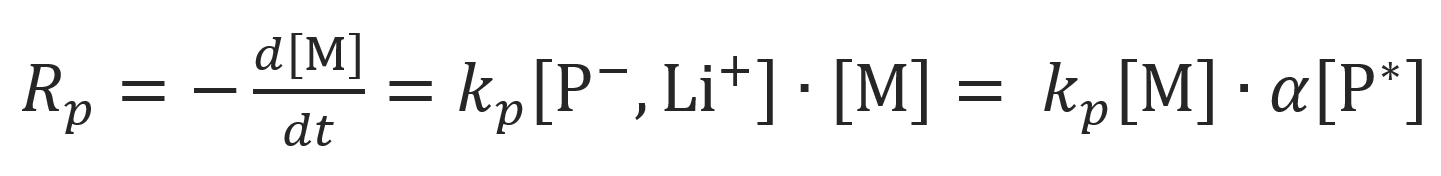
where [M] is the concentration of monomer, k_p is the rate constant of anionic chain growth, [P*] is the concentration of propagating chain ends and α is the fraction of contact ion pairs. The latter quantity can be calculated from Ostwald's dilution law if the dissociation constant of the dimers, K_diss, is known:

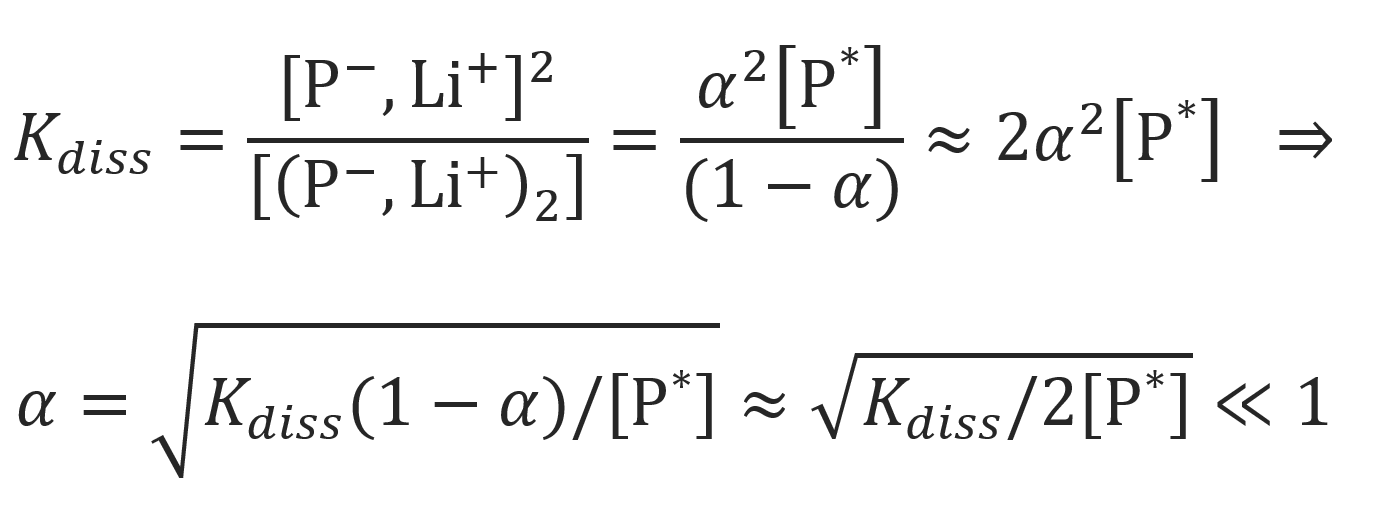
Using this result, the rate of polymerization may be wriiten in the form

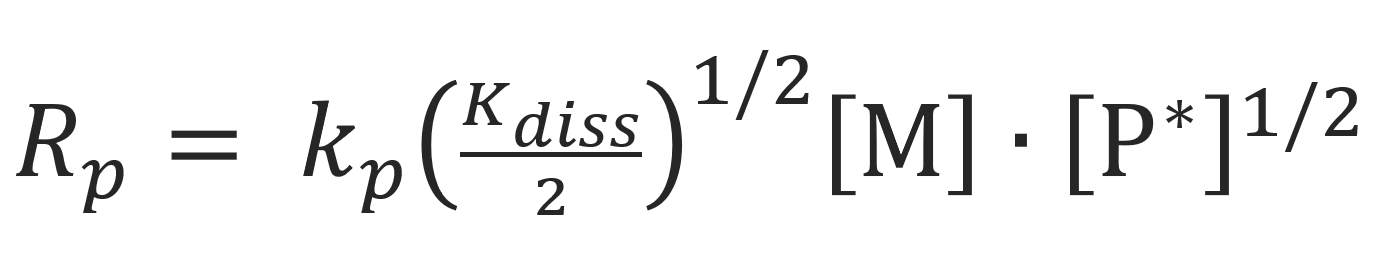
Thus, when contact ion pairs dominate chain growth, the reaction order with respect to the propagating chain ends is approximately 0.5.

Model 2: Nonpolar Monomers in Polar Solvents

The mechanism of anionic propagation depends not only on the polymerization conditions but also on the nature of the solvent and monomer.¹⁰ In a rather polar organic solvent such as dimethoxyethane (DME), tetrahydrofuran (THF) or 3-methyltetrahydrofuran, contact ion pairs, solvent-separated ions pairs, and free (solvated) carbanions exist in a dynamic equilibrium. As has been shown by Schmidt and Schulz, conditions can be found under which the polymerization takes place mainly via one of the two types of ion pairs.⁷ For example, in anionic polymerization of styrene in THF with styryllithium, contact ion pairs are the most abundant ion pairs which are in equilibrium with free ions.⁶ Although the concentration of the latter is rather small, their contribution to the overall rate of propagation can be significant since the rate constant of free carbanions is much larger than that of ion pairs.

Assuming that the contribution of solvent-separated ions pairs to chain growth is negligible, the rate of polymerization is given by

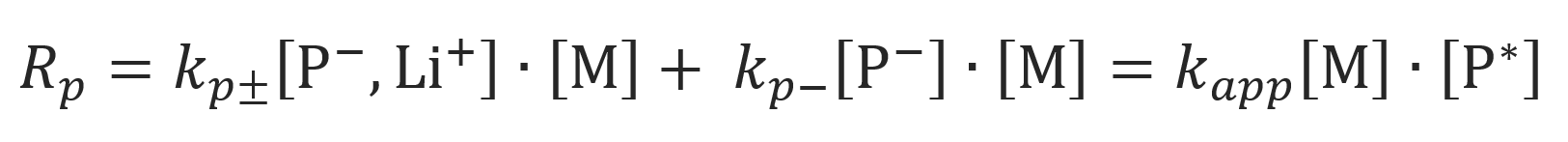
where k_app is the apparent rate constant of propagation:

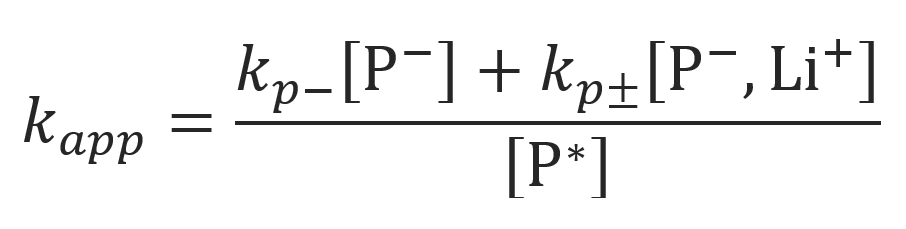
The mole fractions of free ions and ion pairs participating in the propagation are α and 1 − α, respectively. Both quantities can be calculated from Ostwald's dilution law, using the dissociation constant K_diss and and the total concentration of active growth centers [P*]:

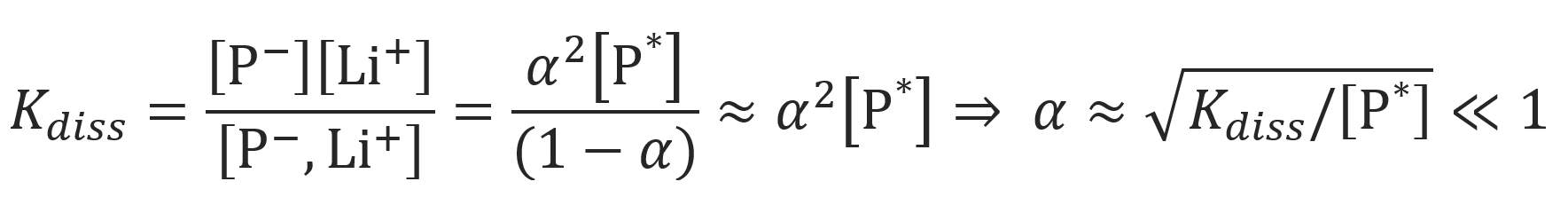
Where we assumed [P^-] = [Li⁺] and [P^-, Li⁺] >> [P^-] so that (1 - α) ≈ 1. Then the apparent rate constant k_app can be rewritten as¹⁰

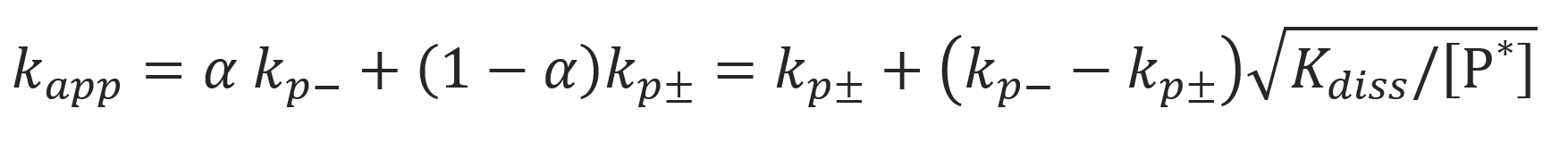
Then the slope of a plot of apparent rate constant k_p,app versus total number of propagating chain ends [P*] equals (k_p- − k_p±)√K_diss and the intercept the corresponding k_p± (Szwarc-Schulz plot).⁶

Alvarino et al.⁹ investigated the more general case that (a) contact ion pairs, (b) solvent separated ion pairs and (c) free carbanions participate in the anionic polymerization:

For this case the overall rate of polymerization, R_p, reads

Then the experimentally determined apparent rate constant can be separated into three terms:⁹

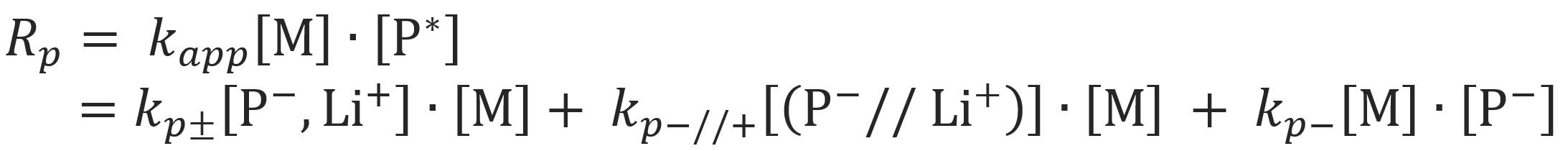
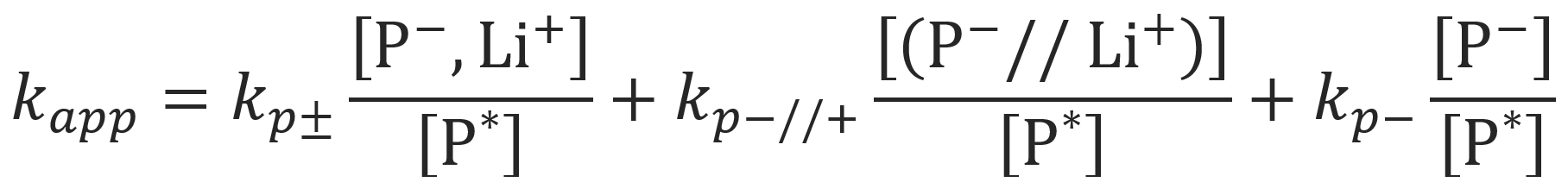
Using the dissociation constants K₁ = [(P^-//Li⁺)] / [(P^-,Li⁺)] and K₂ = [P^-]²/ [(P^-//Li⁺)], the apparent rate constant can be written as:

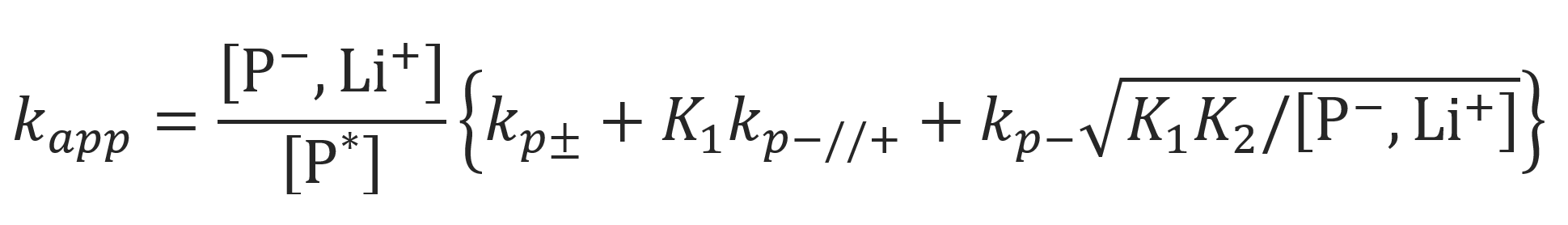
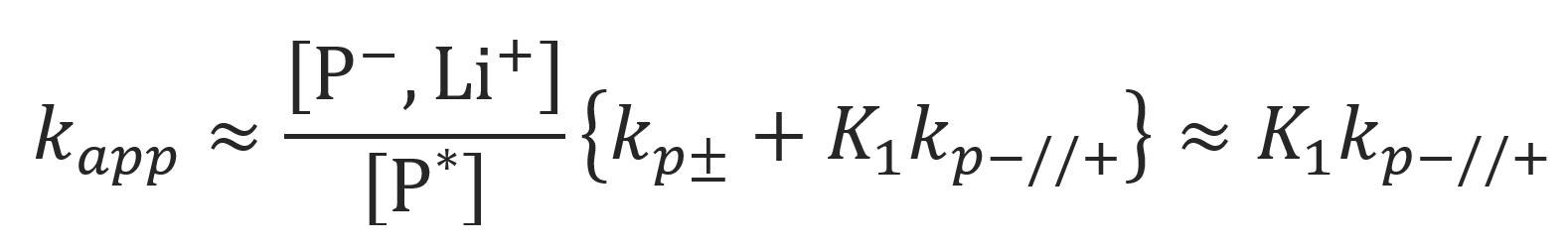
Model 3: Polar Monomers in Polar Solvents

Polar monomers such (meth)acrylates are typically polymerized in polar solvents due to their better solubility. In these solvents, the carbanions are aggregated to various degrees. For example, metal ester enolates, which are formed when (meth)acrylate molecules react with ion pairs of organometallic initiators, form dimeric or tetrameric self-aggregates.⁸ These aggregates are in a dynamic equilibrium with the non-aggregated ion pairs (unimers).

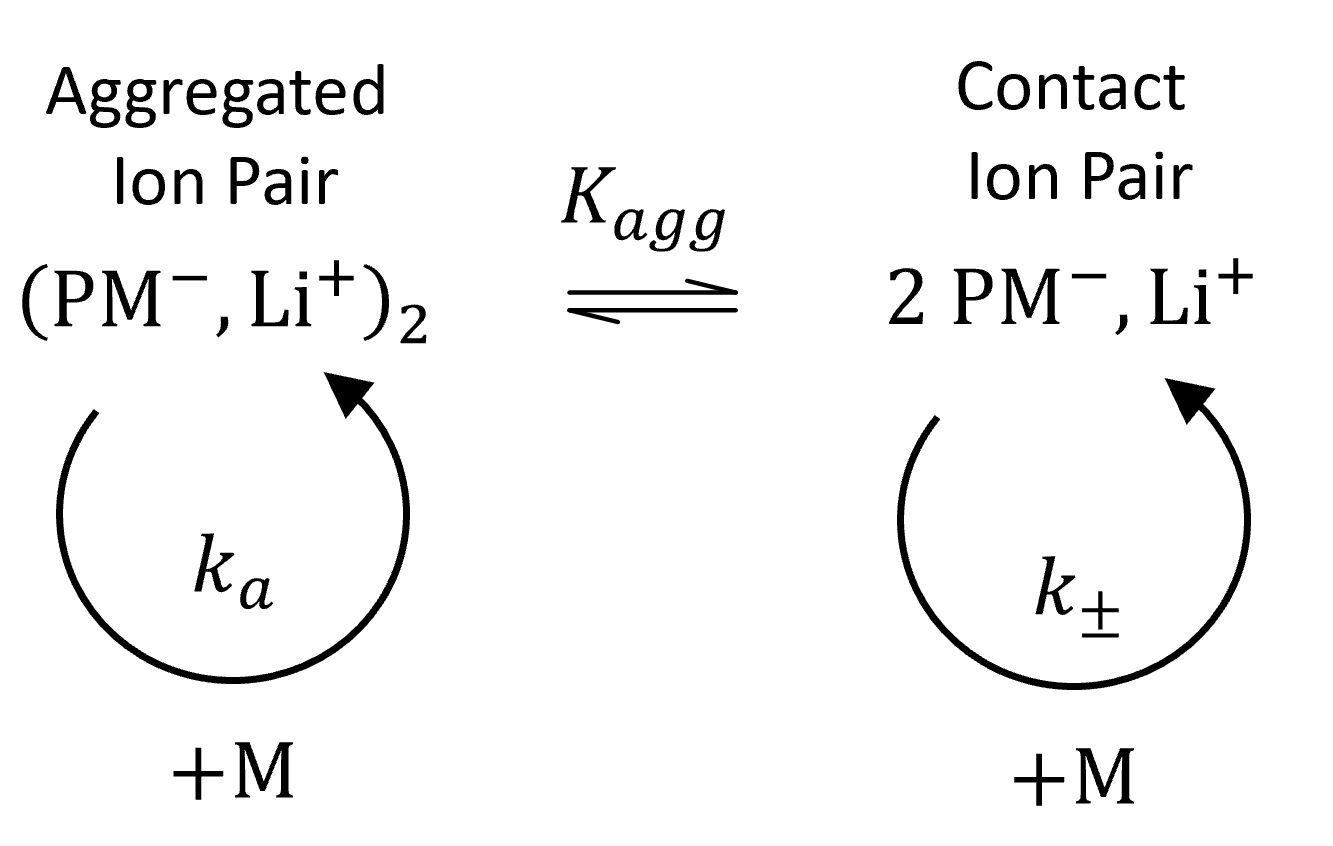
The total rate of propagation is determined by the mole fraction of non-aggregated ion pairs, α, and by the rate constants of the ion pairs, k_p±, the aggregated ion pairs, k_pa:

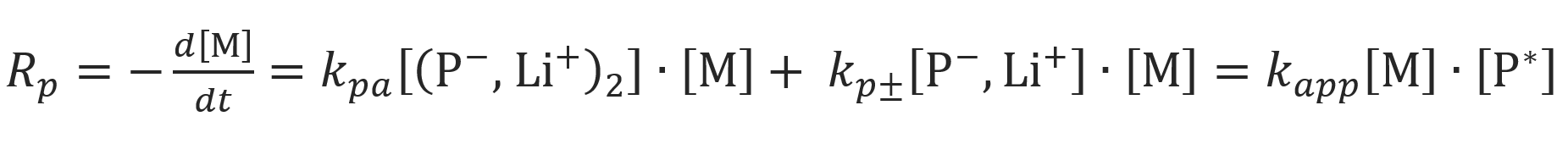
where

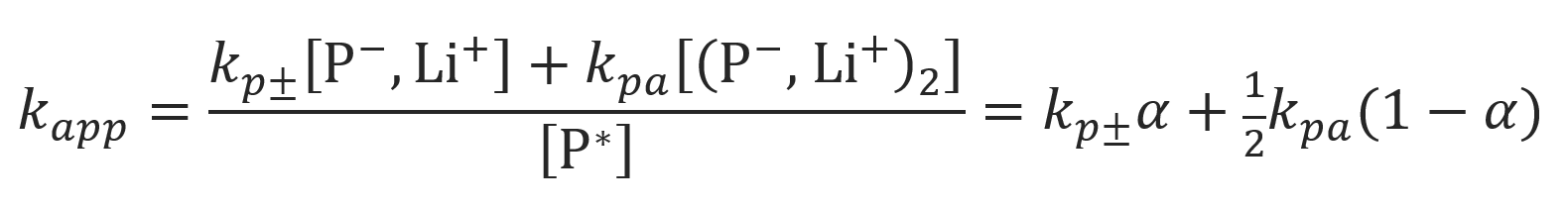
The mole fraction of non-aggregated ion pairs and their rate constant can be calculated from Ostwald's dilution law, using the total concentration of active growth centers [P*] and the aggregation constant K_agg:

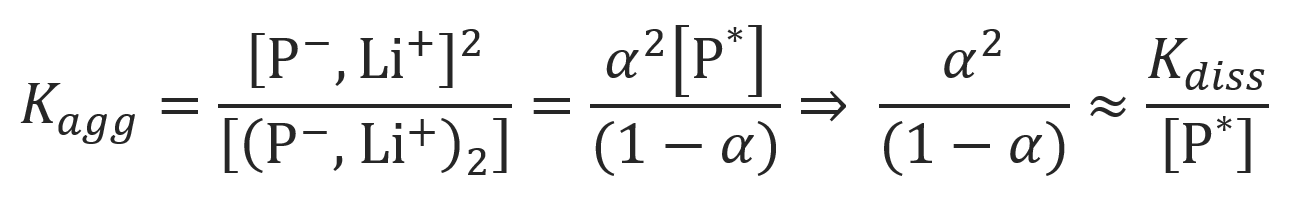
The equation above can be solved for the fraction of non-associated ion pairs (see ref. 6 and references therein):

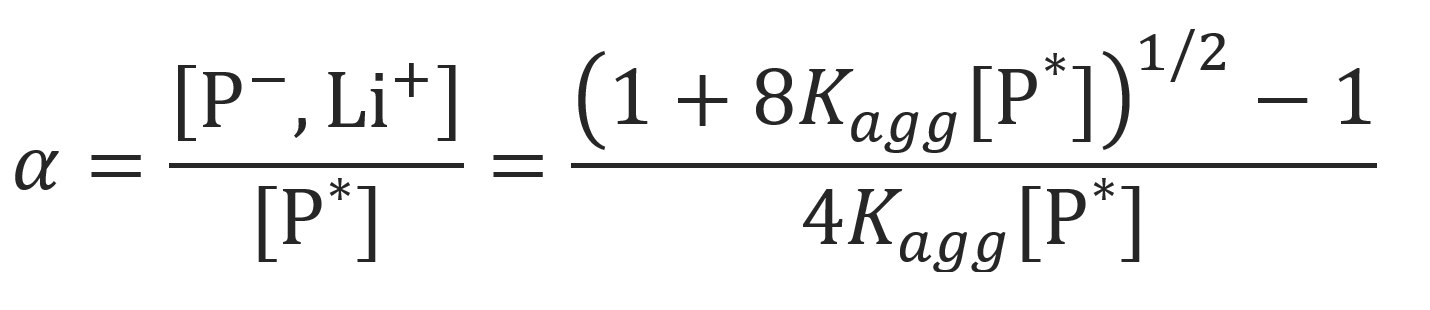
For the case k_p± α >> k_pa (1-α) and K_agg [P*] >> 1, the equation above simplifies to

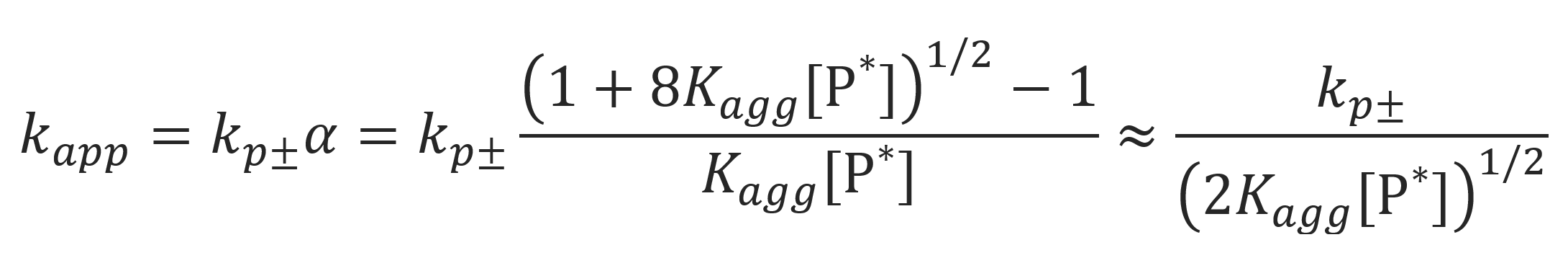
Using this result, the rate of polymerization becomes

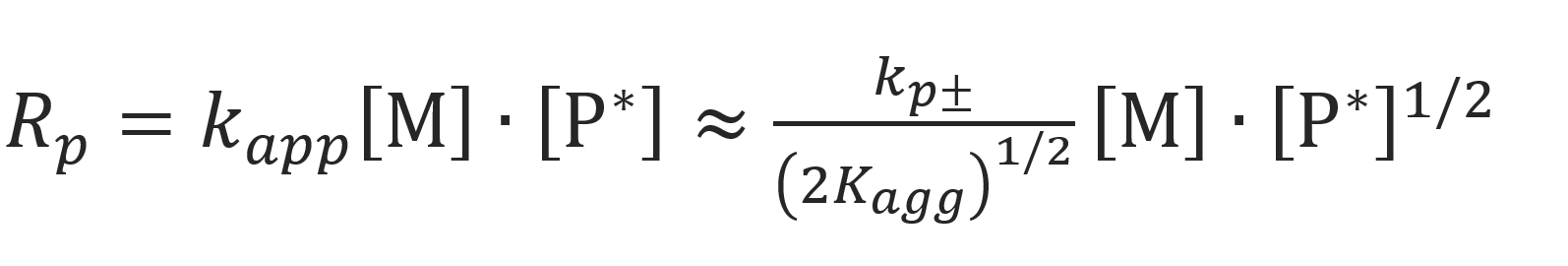
Thus, when non-aggregated ion pairs dominate propagation, the reaction order is approximately 1/2 with respect to [P*].

References & Notes:

1. Raymond M. Fuoss, J. Am. Chem. Soc., 80, 19, 5059 - 5061 (1958)

2. S. Winstein, E. Clippinger, A.H. Fainberg, R. Heck, G.C. Robinson, J. Am. Chem. Soc.,
   78, 2, 328 - 335 (1956)

3. R.A. Marcus, ; N. Sutin, Biochimica et Biophysica Acta, 811, 265-322 (1985)

4. K. Fumino, P. Stange, V. Fossog, R. Hempelmann, R. Ludwig, Angew. Chem., 125, 12667 - 12670 (2013)

5. D.J. Worsfold, S. Bywater, Can. J. Chem., Vol. 38, 1891 (1960) & Vol. 42, 2884 (1964)

6. D. Baskaran, A.H.E. Mueller, Prog. Polym. Sci., 32, 173-219 (2007)

7. B.J. Schmitt, G.V. Schulz, Europ. Poly. J., 11, 2, 119-130 (1975)

8. P. Vlcek, L. Lochmann, Prog. Polym. Sci., 24, 793-873 (1999)

9. J.M. Alvarino, M. Chmelir, B.J. Schmidt, and G.V. Schulz, J. Polym. Sci.: Sympos No. 42,
   155 - 162 (1973)

10. The ion pair rate constant depends on the radius of the counterion; it decreases in tetrahydrofuran (THF) for alkali counterions in the order Li < Na < K < Cs but decreases
    in the reverse order in dioxane.¹¹

11. Johannes Smid, J. Poly. Sci.: Part A: Poly. Chem., Vol. 42, 3655 - 3667 (2004)